CF1581B Diameter of Graph 题解
Content
\(\textsf{CQXYM}\) 想要构造一个包含 \(n\) 个点和 \(m\) 条边的无向连通图,并且他希望这个图满足下列条件:
- 该图中不存在重边和自环。也就是说,一条边应该连接两个不同的顶点,且两个点之间最多只能连一条边。
- 该图的直径严格小于 \(k-1\)。
定义:
- 一个图中两个节点之间的距离是以这两个点为端点的路径经过的最小边数。
- 一个图的直径是任意两点之间距离的最大值。
\(\textsf{CQXYM}\) 想知道他能不能够造出这样一个图。由于他还忙于其他事情,于是就把这个任务交给了你。
数据范围:\(t\) 组数据,\(1\leqslant t\leqslant 10^5\),\(1\leqslant n\leqslant 10^9\),\(0\leqslant m,k\leqslant 10^9\)。
Solution
非常牛的一道分类讨论题。
首先,任何一个图的直径最少是 \(0\)(当且仅当 \(n=1\) 时成立),因此有 \(k-1>0\Rightarrow k>1\)。因此只要 \(k\leqslant 1\),就一定不能构造出满足题目要求的图,排除掉这一类。
排除掉这一类,我们再来看 \(n=1\) 时的情况,此时,由于图不存在重边和自环,因此必须要满足 \(m=0\)。所以当 \(n=1\) 的时候只需要判断是否有 \(m=0\) 成立。
然后就到了关键的 \(n>1\) 这一部分了。众所周知,一个 \(n\) 个点的图要变成联通的,最少需要 \(n-1\) 条边(此时它是一棵树),而且要保证不存在重边和自环的话,由于每个点最多能向 \(n-1\) 个点连边,但是不难发现,这样算的话每条边会重复计算 \(2\) 次。因此,满足条件的 \(n\) 个点的图最多边数为 \(\frac {n(n-1)}2\)。因此可以首先排除 \(m\) 不在 \([n-1,\frac{n(n-1)}2]\) 这个区间内的情况,此时一定不能构造出满足题目要求的图。
然后我们再分成 \(m\in[n-1,\frac{n(n-1)}2)\) 和 \(m=\frac{n(n-1)}2\) 这两个部分来讨论。
首先,我们来看,这是 \(m=n-1\) 的时候能够构造出来的直径最短的图的例子。
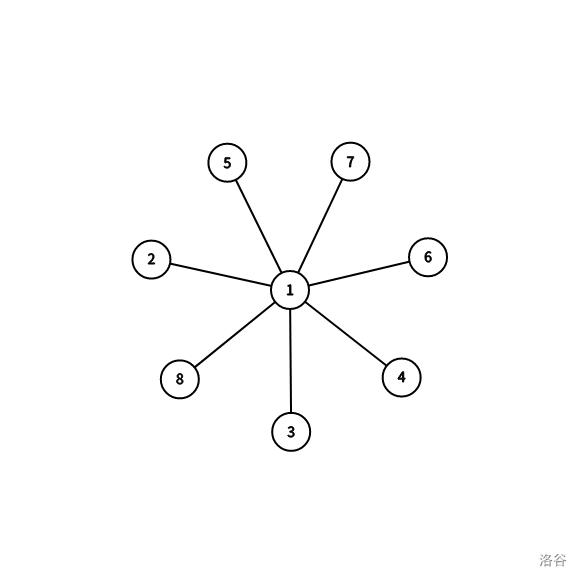
这种一个点连向其他所有点的树,我们称之为菊花图。可以看到,菊花图的直径为 \(2\),而非完全图不能做到一个点可以仅通过一条边到达其他点,因此,当 \(m\in[n-1,\frac{n(n-1)}2)\) 时,直径最小是 \(2\)。对应可以算出 \(2<k-1\Rightarrow k>3\)。
而当 \(m=\frac{n(n-1)}2\) 的时候,此时图变成了完全图,可以做到一个点仅通过一条边到达其他点,因此其直径为 \(1\),对应可以算出 \(1<k-1\Rightarrow k>2\)。
对应情况分类讨论判断即可通过此题。
Code
namespace Solution {
iv Main() {
MT {
ll n, m, k;
read(n, m, k);
if(n == 1) {
if(!m && k >= 2) YES; //赛时由于这里没有写 k >= 2 惨遭暴毙
else NO;
}
else if(m < n - 1) NO;
else if(m >= n - 1 && m < n * (n - 1) / 2) {
if(k <= 3) NO;
else YES;
} else if(m == n * (n - 1) / 2) {
if(k <= 2) NO;
else YES;
} else NO;
}
return;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号