数据结构-栈与队列

栈

---

栈的基本概念

---

• 栈是一种特殊的线性表，其特殊性体现在元素插入和删除运算上，他的插入和删除运算仅限定在线性表的某一端进行，不能在表中间和另一端进行。

• 栈的插入操作称之为进栈（入栈、Push）

• 栈的删除操作称之为出栈（退栈，Pop）

• 允许进行插入和删除的一端称为栈顶，另一端称为栈底

• 处于栈顶位置的数据元素称为栈顶元素

• 不含任何数据元素的栈称为空栈

栈的模型示意图：

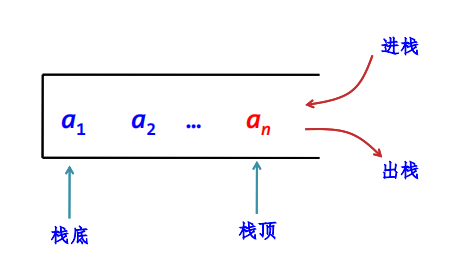
由于栈的数据元素进出的特点，栈又称之为先进后出LIFO(Last In First Out)或先进后出FILO（First In Last Out）线性表。

栈的ADT运算

* 初始化栈InitStack(S)。建立一个空栈S
* 销毁栈DestroyStack(S)。释放栈S占用的内存空间
* 进栈Push(S, x)。将元素x插入栈S中，使x成为栈S的栈顶元素
* 出栈Pop(S, x)。当栈S不空时，将栈顶元素赋给x，并从栈中删除当前栈顶
* 取栈顶元素GetTop(S)。若栈S不空，取栈顶元素x并返回1；否则返回0
* 判断栈空StackEmpty(S)。判断栈S是否为空栈

栈的顺序存储结构

• 栈的顺序存储结构称为顺序栈

• 顺序栈通常由一个一维数组data和一个记录栈顶元素位置的变量top组成

• 习惯上将栈底放在数组下标小的那端，栈顶元素由栈顶指针top指向

类型声明如下：

// ------栈的顺序存储结构表示----------
#define STACK_INIT_SIZE 100 // 存储空间初始分配量
#define STACK_INCREMENT 10 // 存储空间分配增量

typedef char ElemType;

typedef struct {
  ElemType *base; // 栈底指针
  ElemType *top; // 栈顶指针
  int stacksize; // 栈空间大小
} SqStack;

//base表示栈底指针，栈底固定不变，栈顶随着进栈和出栈操作而变化
//用top表示当前栈顶位置
//用top == base作为栈空的标记，每次top指向栈顶数组中的下一个存储位置

对于顺序栈S（可通过动态申请空间得到其存储空间），包含以下四个元素：

栈空：S.top == S.base;
栈满：S.top - S.base >= S.stacksize;
元素e进栈操作：*(S.top)++ = e;
元素e出栈操作：e = *--S.top;

可以通过下面几个图来理解：

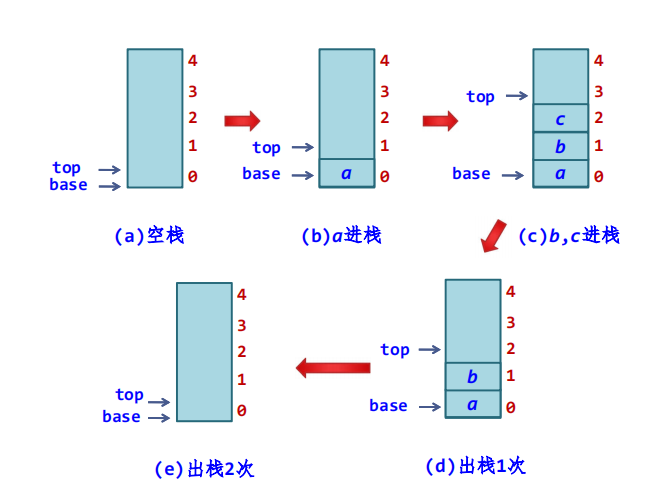
基本算法设计

初始化栈

思路分析:主要操作为通过动态申请所需要的存储空间，并且初始化相关参数

void InitStack(SqStack &S)
{
  //构造一个空栈S
  if(!(S.base = (ElemType *)malloc (STACK_INIT_SIZE*sizeof(ElemType))))
  exit(OVERFLOW);

  S.top == S.base;
  S.stacksize = STACK_INIT_SIZE;
}

销毁栈

释放初始化栈时申请的空间，值得注意的是，应将相关参数置为初始值，防止野指针和随机值。

void DestroyStack(SqStack &S)
{
    // 销毁栈S，S不再存在
    free(S.base);
    S.base = NULL;  //指针置空
    S.top = NULL; 
    S.stacksize = 0;//Size 置为0
}

进栈算法

数据进栈，top移动，base保持不变，注意判断是否溢出

void Push(SqStack &S,ElemType e)
{
  if(S.top - S.base >= S.stacksize)
      exit(OVERFLOW);    //这里不再使用realloc重新申请空间

  *(S.top)++ = e;
}

如果大家想通过realloc函数重新申请空间，来避免出现溢出问题,这里给出相关代码：

if(S.top - S.base >= S.stacksize) { // 栈满，追加存储空间
    S.base = (ElemType *)realloc(S.base, (S.stacksize 
+ STACK_INCREMENT) * sizeof(ElemType));
    if(!S.base)
        exit(OVERFLOW); // 存储分配失败
    S.top = S.base + S.stacksize;
    S.stacksize += STACK_INCREMENT;
}

出栈运算

移动top指针，但需要判断是否栈为空

Status Pop(SqStack &S, ElemType &e)
{
      // 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；
      // 否则返回ERROR
      if(S.top == S.base)
          return ERROR;
      e = *--S.top;
      return OK;
}

取栈顶元素算法

通过top指针，取出栈顶元素,不过这里，top指针并没有发生改变

Status GetTop(SqStack S, ElemType &e)
{
    // 若栈不空，则用e返回S的栈顶元素，并返回OK；
    // 否则返回ERROR
    if(S.top > S.base) {
      e = *(S.top - 1);
      return OK;
    }
    else
      return ERROR;
}

判断栈空元素

若栈为空，返回1，否则返回0

Status StackEmpty(SqStack S)// 若栈S为空栈，则返回TRUE，否则返回FALSE
{
  return S.top == S.base;

  //或者如下：
  if(S.top == S.base)
      return TRUE;
  else
      return FALSE;
}

链栈存储结构

• 栈的链式存储结构采用某种链表哦结构，栈的链式存储结构简称为链栈

• 这里采用单链表作为链栈，该单链表是不带头节点的

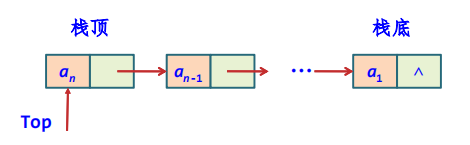
结点声明与算法设计

结点声明：

typedef char ElemType;

typedef struct node {
    ElemType data;
    struct node *next;
} LinkStack;

同样的，和顺序栈一样，我们可以归纳为四个要素：

栈空：top == NULL;
栈满：不考虑
元素x进栈：创建存放元素x的结点p，将其插入到栈顶位置
元素x出栈：置x为栈顶结点的data域，并删除该节点

初始化栈

初始化栈主要操作：用top==NULL标识栈为空栈

void InitStack(LinkStack *&top)
{
  top = NULL;
}

销毁栈

链栈的所有结点空间都是通过malloc函数分配的，在不再需要时需通过free函数释放所有结点的空间。

void DestroyStack(LinkStack *&top)
{
  LinkStack *pre = top,*p;
  if(pre == NULL) return;  //判断是否栈空
  p = pre->next;
  while(p != NULL)
  {
    free(pre);  //释放pre结点
    pre = p;
    p = p->next;  //pre、p同步后移
  }
  free(pre);  //释放尾结点
}

进栈

主要运算：先创建一个新节点，其data域值为x；然后将该节点插入到top结点之后作为栈顶结点。

int push(LinkStack *&top,ElemType x)
{
  LinkStack *p;
  p = (LinkStack *)malloc(sizeof(LinkStack));
  p->data = x;  //创建结点p存放x
  p->next = top;  //插入p作为栈顶结点,头插法
  top = p;
  return 1;
}

出栈

主要操作：将栈顶结点（即top->next所指结点） 的data域值赋给x，然后删除该栈顶结点。

int Pop(LinkStack *&top,ElemType &x)
{
  LinkStack *p;
  if(top == NULL) //栈空，下溢出返回0
    return 0;
  else    //栈不空时出栈元素x并返回1
  {
    p = top;    //p指向栈顶结点
    x = p->data;    //取栈顶元素x
    top = p->next;  //删除结点p
    free(p)    //释放p结点
    return 1;
  }
}

取栈顶元素

主要操作：将栈顶结点（即top->next所指结点） 的data域值赋给x。

int GetTop(LinkStack *top,ElemType &x)
{
  if(top == NULL)//栈空,下溢出时返回0
    return 0;
  else  //栈不空,取栈顶元素x并返回1
  {
    x = top->data;
    return 1;
  }
}

判断栈空

主要操作：若栈为空（即top==NULL）则返回值1，否则返回值0

int StackEmpty(LinkStack *top)
{
  if(top == NULL)
    return 1;
  else 
    return 0;
}

队列

队列的基本概念

• 队列（简称队）也是一种运算受限的线性表，在这种线性表上，插入限定在表的某一端进行，删除限定在表的另一端进行。

• 队列的插入操作称为进队

• 删除操作称为出队

• 允许插入的一端称为队尾

• 允许删除的一端称为队头

• 新插入的元素只能添加到队尾，被删除的只能是排在队头的元素

• 队列的模型示意图

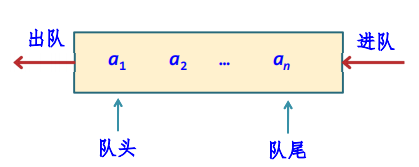
队列是一种先进先出（First In First Out），简称FIFO线性表

• 队列的基本运算

* 初始化队列InitQueue(Q),建立一个空队Q
* 销毁队DestroyQueue(Q),释放队列Q占用的内存空间
* 进队EnQueue(Q, x),将x插入到队列Q的队尾
* 出队DeQueue(Q, x),将队列Q的队头元素出队并赋给x
* 取队头元素GetHead(Q, x)。取出队列Q的队头元素并赋给x，但该元素不出队
* 判断队空QueueEmpty(Q),判断队列Q是否为空

循环队列--队列的顺序表示和实现

• 队列通常有两种存储结构，即顺序存储结构和链式存储结构
• 队列的顺序存储结构简称为顺序队列，它由一个一维数组（用于存储队列中元素）及两个分别指示队头和队尾的变量组成，这两个变量分别称为“队头指针” 和“队尾指针”
• 通常约定：初始化建空队列时，令 front=rear=0。在非空队列中，头指针始终指向队列头元素，而尾指针始终指向rear队列尾元素的下一个位置

顺序队列的类型声明如下

//----------队列的静态存储结构-------------
#define MaxSize 20 //指定队列的容量

typedef struct
{ 
    ElemType data[MaxSize];//保存队中元素
    int front,rear; //队头和队尾指针
} SqQueue;

常规的结构的运算如下：

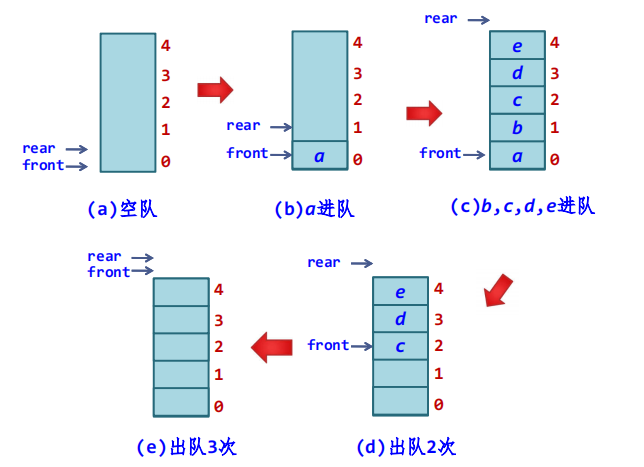
• 图 (a)和(e)都是队空的情况，均满足frontrear的条件，所以可以将frontrear作为队空的条件

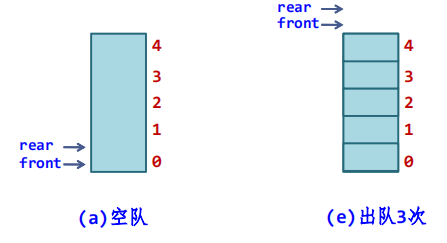
• 那么队满的条件如何设置呢？受顺序栈的启发，似乎很容易得到队满的条件为rear==MAXSIZE。显然这里有问题，因为图 (d)和(e)都满足这个“队满”的条件，而实际上队列并没有满

这种因为队满条件设置不合理而导致的“溢出”称为假溢出，也就是说这种“溢出”并不是真正的溢出，尽管队满条件成立了，但队列中还有多个存放元素的空位置

• 为了能够充分地使用数组中的存储空间，可以把数组的前端和后端“假想地”连接起来，形成一个环形的表，即把存储队列元素的表从逻辑上看成一个环

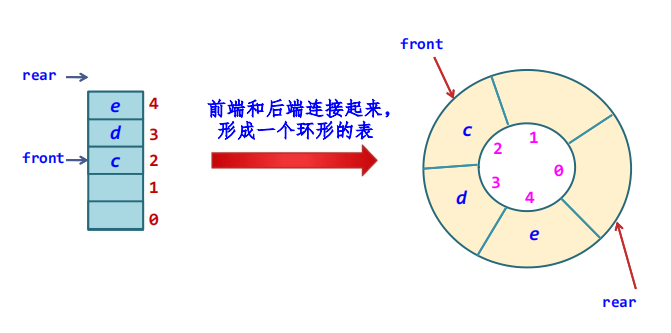
称之为循环队列

我们先给出一组图

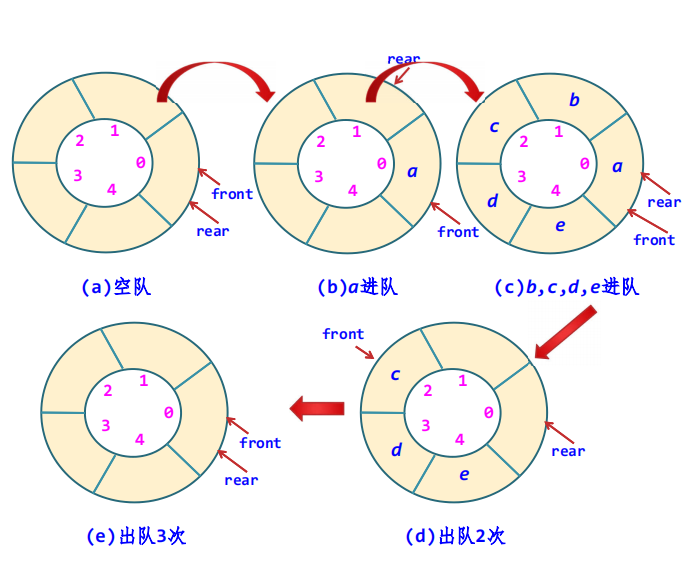
根据图片，我们可以得出以下结论：

队头指针进1：front=(front+1) MOD MAXSIZE
队尾指针进1：rear=(rear+1) MOD MAXSIZE

• 但，我们仍无法区分队空和队满，图(a)、(c)和(e)都满足条件front==rear

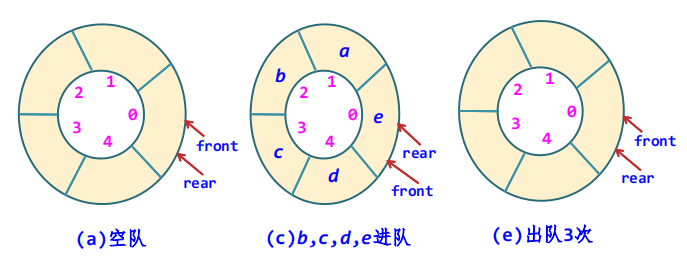
因此，我们给出以下规定

* 仍设置队空条件为front==rear
* 将队满条件设置为(rear+1) MOD MAXSIZE==front
* 当rear指到front的前一位置时就认为队列满了

//第二条的意思是,首先试探进队，若达到队头指针位置，则认为队满！

由这个规定，显然在这样设置的队满条件下，队满条件成立时队中还有一个空闲单元，也就是说这样的队中最多只能进队MAXSIZE-1个元素

总结一下，四要素如下：

队空条件：Q.front==Q.rear
队满条件：(Q.rear+1)%MaxSize==Q.front
进队：
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%MaxSize；
出队：
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%MaxSize;

声明与算法

声明

//----------循环队列 --顺序存储结构-----------------------
#define MAXQSIZE 100 // 最大队列长度+1

typedef struct {
    ElemType *base; // 初始化的动态分配存储空间
    int front; // 头指针，若队列不空，指向队列头元素
    int rear; // 尾指针，若队列不空，指向队列尾元素的下一个位置
} SqQueue ;

循环队列的基本算法

初始化

主要操作：指定sq.front=sq.rear=0

void InitQueue(SqQueue &Q)
{ // 构造一个空队列Q
    Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType));
    if(!Q.base) // 存储分配失败
        exit(OVERFLOW);
    Q.front = Q.rear = 0;
}

销毁

顺序队的内存空间是动态申请得到的，在不再需要时由申请者主动释放其空间

void DestroyQueue(SqQueue &Q)
{
    // 销毁队列Q，Q不再存在
    if(Q.base)
        free(Q.base);
    Q.base = NULL;
    Q.front = Q.rear = 0;
}

入队列算法

主要操作：先判断队列是否已满，若不满，在队尾指针位置存放x，然后循环加1

Status EnQueue(SqQueue &Q, QElemType e)
{    // 插入元素e为Q的新的队尾元素
    if((Q.rear + 1) % MAXQSIZE == Q.front) // 队列满
        return ERROR;
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear + 1) % MAXQSIZE;
    return OK;
}

出队列算法

主要操作：先判断队列是否已空，若不空，将队头指针位置的元素值赋给x，然后对头指针循环加1。

Status DeQueue(SqQueue &Q, QElemType &e)
{
    // 若队列不空，则删除Q的队头元素，用e返回其值
    // 并返回OK；否则返回ERROR
    if(Q.front == Q.rear) // 队列空
        return ERROR;
    e = Q.base[Q.front];
    Q.front = (Q.front + 1) % MAXQSIZE;
    return OK;
}

取队头元素运算算法

主要操作：先判断队列是否已空，若不空，将队头指针前一个位置的元素值赋给x

Status GetHead(SqQueue Q, QElemType &e)
{
    // 若队列不空，则用e返回Q的队头元素，并返回OK；
    // 否则返回ERROR
    if(Q.front == Q.rear) // 队列空
        return ERROR;
    e = Q.base[Q.front];
    return OK;
}

判断队空算法

主要操作：若队列为空，则返回1；否则返回0

Status QueueEmpty(SqQueue Q)
{
    // 若队列Q为空队列，则返回TRUE；否则返回FALSE
    if(Q.front == Q.rear) // 队列空的标志
        return TRUE;
    else return FALSE;
}

链队列--队列的链式表示和实现

• 队列的链式存储结构简称为链队列

• 这里采用的链队列是一个同时带有队头指针front和队尾指针rear的单链表

• 队头指针指向头结点，队尾指针指向队尾结点即单链表的尾结点，并将队头和队尾指针结合起来构成链队结点

• 链队列的基本结构

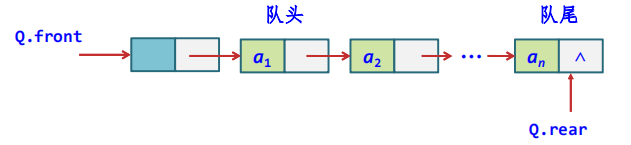
• 结点结构：

//数据结点
typedef struct QNode
{ 
    ElemType data; //存放队中元素
    struct QNode *next; //指向下一个结点
} QNode, *QueuePtr; //数据结点类型

//链队结点

typedef struct
{ 
    QNode *front; //队头指针
    QNode *rear; //队尾指针
} LinkQueue; //链队结点类型

• 链队列的四个要素:

队空条件：Q.front->next == NULL;
队满条件：不考虑
进队操作：创建结点p,将其插入到队尾，并由Q.rear指向它
出队操作：删除队头的结点

相关算法实现

初始化队列

主要操作：创建链队列头结点，并置rear和front指向头结点，且指针域为NULL

void InitQueue(LinkQueue &Q)
{
    // 构造一个空队列Q
    if(!(Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode))))
        exit(OVERFLOW);
    Q.front->next = NULL;
}

销毁队列

依次释放单链表的结点即可

void DestroyQueue(LinkQueue &Q)
{
    // 销毁队列Q(无论空否均可)
    while(Q.front) {
        Q.rear = Q.front->next;
        free(Q.front);
        Q.front = Q.rear;
    }
}

入队列算法

主要操作：创建一个新结点，将其链接到链队的末尾，并由rear指向它

void EnQueue(LinkQueue &Q, QElemType e)
{
    // 插入元素e为Q的新的队尾元素
    QueuePtr p;
    if(!(p = (QueuePtr)malloc(sizeof(QNode)))) //存储分配失败
        exit(OVERFLOW);
    p->data = e;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
}

出队列算法

主要操作：将front->next结点的data域值赋给e，并删除该结点

Status DeQueue(LinkQueue &Q, QElemType &e)
{
    // 若队列不空，删除Q的队头元素，用e返回其值，并返回OK
    // 否则返回ERROR
    QueuePtr p;
    if(Q.front == Q.rear)  //栈为空
        return ERROR;
    p = Q.front->next;  //p指向front的下一个结点
    e = p->data;
    Q.front->next = p->next;
    if(Q.rear == p)  //如果删除后为空，则返回初始位置
        Q.rear = Q.front;
    free(p);
    return OK;
}

取队头元素算法

将对头结点的data域值赋给e

Status GetHead(LinkQueue Q, QElemType &e)
{
    // 若队列不空，则用e返回Q的队头元素，并返回OK
    // 否则返回ERROR
    QueuePtr p;
    if(Q.front == Q.rear) //队列为空
        return ERROR;
    p = Q.front->next;
    e = p->data;
    return OK;
}

判断队空算法

主要操作：若链队为空，则返回1；否则返回0。

Status QueueEmpty(LinkQueue Q)
{
    // 若Q为空队列，则返回TRUE，否则返回FALSE
    if(Q.front->next == NULL)
        return TRUE;
    else
        return FALSE;
}