损失函数

一.为什么要有损失函数

想象你在学习射箭：

你第一次射箭，箭飞到了靶子的左上角。

你第二次射箭，箭飞到了靶子的右下角。

你第三次射箭，箭差点脱靶。

现在问题来了：

你怎么知道自己射得好不好？

你怎么知道下一次该往哪个方向调整？

这时候就需要一个“裁判”来告诉你：

“第一箭，偏左上30厘米。”

“第二箭，偏右下20厘米。”

“第三箭，偏右50厘米，太远了！”

这个“裁判”就是损失函数。

二、损失函数的作用

1. 衡量“犯错程度”的尺子

没有损失函数：模型猜对了还是猜错了？不知道！

有损失函数：可以精确地告诉模型“你错了多少”。

例子：预测房价

真实房价：100万

模型A预测：110万（误差10万）

模型B预测：150万（误差50万）

损失函数会告诉你：模型B比模型A错得更离谱。

2. 告诉模型“往哪改”的导航

损失函数不仅告诉你错了，还告诉你该怎么改正。

就像射箭教练说：“你射得太偏左了，下次往右一点。”

在神经网络中，这个“往右一点”就是梯度，它告诉每个参数：“你应该变大一点还是变小一点？”

3. 比较不同模型的“成绩单”

你想买两个AI模型来预测股票。

怎么知道哪个更好？

让它们都用同一份历史数据预测，然后用损失函数打分：

模型A的损失：10分（分数越低越好）

模型B的损失：50分

结论：模型A更好。

4.损失函数的原理——核心就一句话

损失函数的本质：

用一个数字，概括模型的所有错误。

怎么做到的？

对每个预测错误，计算一个“扣分”。

把所有“扣分”加起来或平均。

得到一个总分，这就是损失值。

关键思想：

损失值 越大 → 模型越差

损失值 越小 → 模型越好

目标：让损失值尽可能小

三.欧氏距离

1.说明

欧氏距离就是我们在现实世界中用尺子量的“直线距离”。比如地图上两点之间的最短距离。

例子1：地图导航
你在天安门广场（A点）

目的地是王府井（B点）

直线飞过去有多远？这就是欧氏距离

例子2：游戏中的距离
玩《英雄联盟》或《王者荣耀》：

你的英雄在位置 (10, 20)

敌方英雄在位置 (40, 50)

你想知道“离敌人有多远”，游戏算的就是欧氏距离

2.数学定义

1.二维空间
在平面上，两点 x1, y1 和 x2, y2 的欧氏距离：数学定义

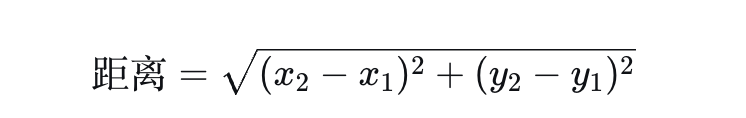
2. 三维空间

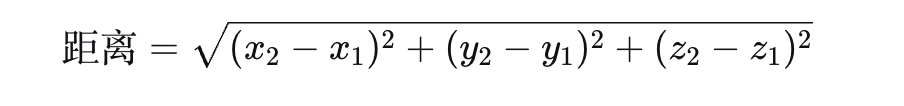
这就是我们中学学的“勾股定理”：
3. 高维空间（n维）

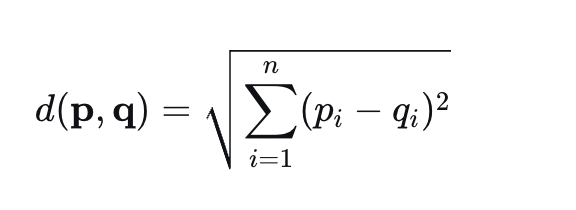
机器学习中的应用：

# 计算新样本与所有训练样本的欧氏距离
新样本 = [170, 65]  # 身高170cm，体重65kg
样本1 = [165, 60]  # 距离 = √[(170-165)² + (65-60)²] = √(25+25)=7.07
样本2 = [180, 80]  # 距离 = √[(170-180)² + (65-80)²] = √(100+225)=18.03

四.几种损失函数

最直观的理解：它就是“用尺子量错误”

1.均方误差

均方误差（Mean Squared Error, MSE） 就是欧氏距离的平方（不开根号）。MSE是损失函数的一种，而且是回归问题中最常用的一种

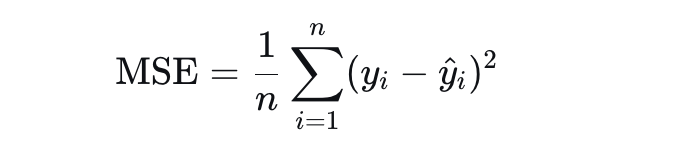
MSE的三个关键特性:
特性1：非负性
MSE ≥ 0，永远不会为负
MSE = 0：完美预测（所有预测完全正确）
MSE > 0：有预测误差
MSE越小越好：目标是让MSE趋近于0

特性2：对称性
高估和低估同样惩罚：
真实值100，预测90（低估10） → 惩罚100
真实值100，预测110（高估10） → 惩罚100
惩罚相同！

特性3：可导性
MSE处处可导，梯度简单：

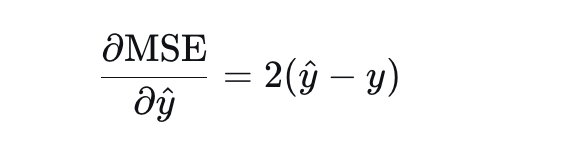
2.欧氏距离（欧氏距离可以作为损失函数使用）

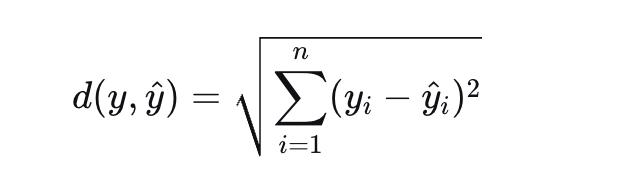
欧氏距离去掉根号就是平方距离，再取平均就是MSE
计算示例
预测3个人的体重：

真实体重：[60, 70, 80] 公斤

预测体重：[65, 68, 75] 公斤

一步步计算：

单个误差：

第1人：60-65 = -5 → 平方 = 25

第2人：70-68 = 2 → 平方 = 4

第3人：80-75 = 5 → 平方 = 25

误差平方和：25 + 4 + 25 = 54

MSE = 54 ÷ 3 = 18

欧氏距离 = √54 ≈ 7.348

3.交叉熵损失

比喻：考试评分老师
假设一道判断题（对/错），正确答案是"对"。

学生A：预测"对"的概率 0.9，"错"的概率 0.1
学生B：预测"对"的概率 0.6，"错"的概率 0.4
学生C：预测"对"的概率 0.1，"错"的概率 0.9
学生A：-log(0.9) = 0.105 （扣0.105分）
学生B：-log(0.6) = 0.511 （扣0.511分）
学生C：-log(0.1) = 2.303 （扣2.303分）

规律：你越自信地猜错，老师越生气！

交叉熵的数学定义

1. 二分类情况（两个类别）
   真实标签：y ∈ {0, 1}
   预测概率：ŷ = P(y=1)

交叉熵损失：L = -[y·log(ŷ) + (1-y)·log(1-ŷ)]

# 情况1：真是猫(y=1)，预测0.9
loss = -[1×log(0.9) + 0×log(0.1)] = -log(0.9) ≈ 0.105

# 情况2：不是猫(y=0)，预测0.1  
loss = -[0×log(0.1) + 1×log(0.9)] = -log(0.9) ≈ 0.105

# 情况3：真是猫(y=1)，但预测0.1（自信地猜错！）
loss = -[1×log(0.1) + 0×log(0.9)] = -log(0.1) ≈ 2.303

2. 多分类情况（多个类别）
   真实标签：one-hot编码，如[0,0,1,0,0]
   预测概率：ŷ = [0.1,0.2,0.6,0.05,0.05]

交叉熵损失：L = -∑ y_i·log(ŷ_i)
只算真实类别那个：L = -log(ŷ_true_class)
举例：

# 真实：数字"7" → one-hot: [0,0,0,0,0,0,0,1,0,0]
# 预测概率：[0.01,0,0,0.1,0,0,0,0.85,0.04,0]

# 只计算第7个位置（真实类别）：
loss = -log(0.85) ≈ 0.162

# 如果预测为"7"的概率很小：
loss = -log(0.01) ≈ 4.605 （惩罚很重！）

为什么交叉熵可以作为损失函数？
条件1：衡量"错误程度" ✅

# 预测准确时损失小
预测概率 = 0.99 → loss = -log(0.99) ≈ 0.01

# 预测错误时损失大  
预测概率 = 0.01 → loss = -log(0.01) ≈ 4.61

# 预测模糊时损失中等
预测概率 = 0.5 → loss = -log(0.5) ≈ 0.69

条件2：可导（利于优化） ✅

五.损失函数对比

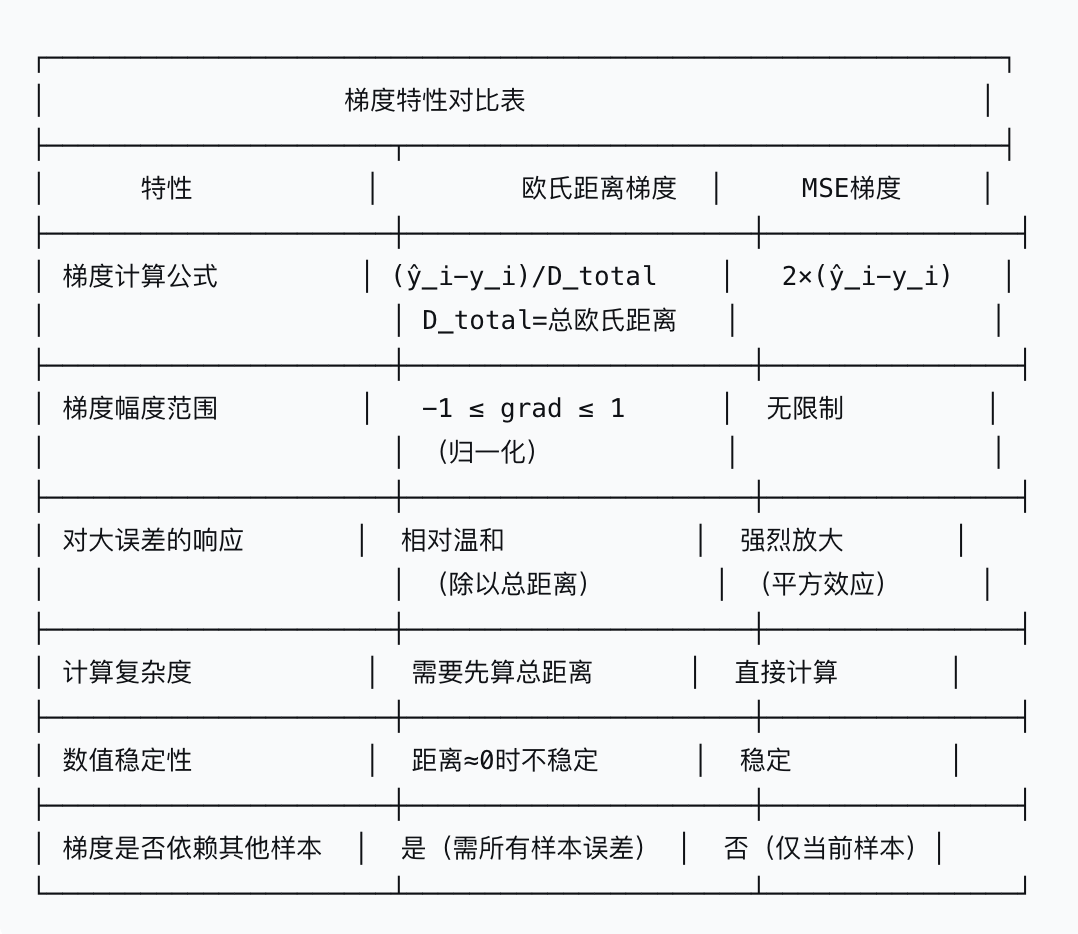
1.欧氏距离损失函数 vs MSE损失的梯度对比

梯度计算公式对比

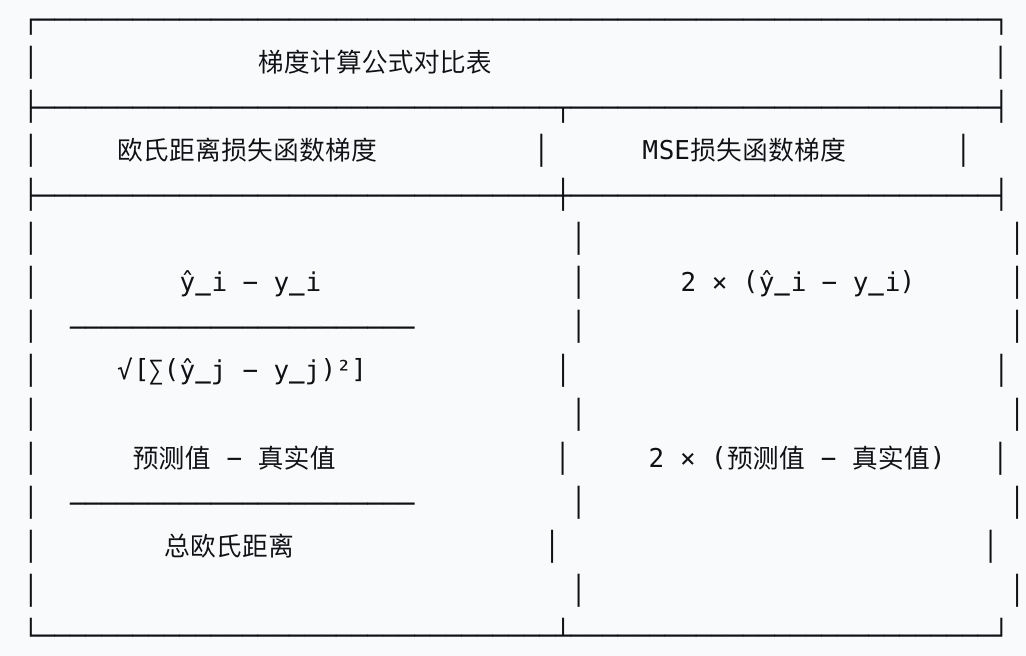
1.欧氏距离损失梯度

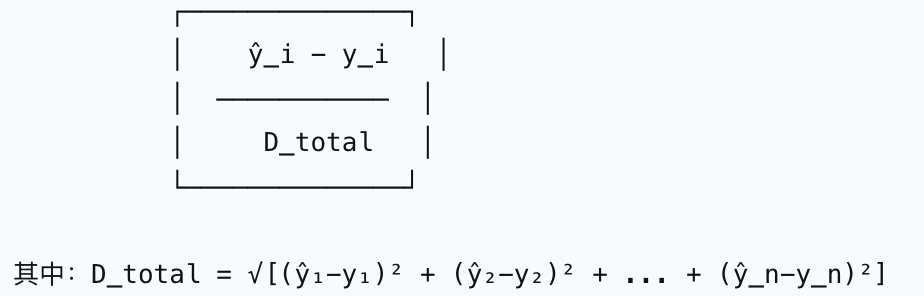
举例：

2.MSE损失梯度

3.对比

Sigmoid + 交叉熵的优势

MSE和交叉熵的梯度

输入特征：x₁, x₂, ..., xₙ
权重和偏置：w₁, w₂, ..., wₙ, b

线性组合：z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

通过Sigmoid激活函数：
ŷ = σ(z)(1-σ(z)) = 1 / (1 + e^{-z})
激活函数sigmoid的导数=σ(z)(1-σ(z))
ŷ是预测概率，范围在(0,1)
MES:
损失函数：L_MSE = (ŷ - y)²

梯度（对z的导数）：
∂L_MSE/∂z = ∂L_MSE/∂ŷ × ∂ŷ/∂z
= 2(ŷ - y) × ŷ(1-ŷ)

实际常简化（系数2被学习率吸收）：
∂L_MSE/∂z ≈ (ŷ - y) × ŷ(1-ŷ)

交叉熵（Cross-Entropy）：
损失函数：L_CE = -[y·log(ŷ) + (1-y)·log(1-ŷ)]

梯度（对z的导数）：
∂L_CE/∂z = ∂L_CE/∂ŷ × ∂ŷ/∂z
= [-y/ŷ + (1-y)/(1-ŷ)] × ŷ(1-ŷ)

数学简化后得到：
∂L_CE/∂z = ŷ - y

输出是连续数值 → 用MSE
输出是概率或类别 → 用交叉熵

举例

我们训练一个AI医生判断X光片是否显示肺炎：

输入：X光片的特征

输出：ŷ = 肺炎概率（0~1）

真实情况：y = 1（有肺炎）或 0（无肺炎）

激活函数：Sigmoid（将医生判断转换为概率）

比较：两种教学方式（MSE vs 交叉熵）
第一阶段：医生完全不懂（初始训练）
第1个病人：确实有肺炎
真实情况：y = 1（有肺炎）
新手医生判断：ŷ = 0.2（20%认为有肺炎，很没把握）
损失函数MSE判断:

损失：L = (0.2 - 1)² = 0.64
梯度：∂L/∂z = (0.2 - 1) × 0.2×(1-0.2) = (-0.8) × 0.16 = -0.128
"""
教授反馈："你判断得太保守了，应该更倾向肺炎一些。"
梯度-0.128意味着：稍微增加权重
"""

损失函数交叉熵判断：

损失：L = -log(0.2) ≈ 1.61
梯度：∂L/∂z = 0.2 - 1 = -0.8
"""
教授反馈："你完全错了！这是明显肺炎，你居然只有20%把握？必须大幅提高判断标准！"
梯度-0.8意味着：大幅度增加权重
"""

第一阶段小结：
MSE：温和指导，医生进步缓慢
交叉熵：严厉纠正，医生快速调整

第二阶段：医生开始有自信
经过几轮学习后：
第10个病人：有肺炎
真实情况：y = 1
医生判断：ŷ = 0.8（80%把握，比较自信）
MSE判断：

损失：L = (0.8 - 1)² = 0.04
梯度：∂L/∂z = (0.8 - 1) × 0.8×0.2 = (-0.2) × 0.16 = -0.032
"""
教授反馈："嗯，还不错，但还可以更准一点。"
"""

交叉熵判断：

损失：L = -log(0.8) ≈ 0.223
梯度：∂L/∂z = 0.8 - 1 = -0.2
"""
教授反馈："接近了，但还有差距，继续提高。"
"""

第二阶段小结：
两位教授反馈相似，因为医生判断比较合理。

第三阶段：关键转折！医生过度自信犯错
第50个病人：其实是严重肺结核，不是肺炎
真实情况：y = 0（不是肺炎）
但医生之前看过很多肺炎病例，形成"有阴影就是肺炎"的错误观念
医生判断：ŷ = 0.95（95%自信是肺炎）
MSE判断：

损失：L = (0.95 - 0)² = 0.9025
梯度：∂L/∂z = (0.95 - 0) × 0.95×0.05 = 0.95 × 0.0475 ≈ 0.045
"""
教授反馈："好像不太对...但也不太确定，你再想想。"
梯度0.045非常小！
"""

交叉熵判断：

损失：L = -log(1-0.95) = -log(0.05) ≈ 2.996
梯度：∂L/∂z = 0.95 - 0 = 0.95
"""
教授拍桌子："大错特错！这不是肺炎！你太武断了！必须彻底改变判断标准！"
梯度0.95非常大！
"""

关键差异：
MSE梯度：∂L/∂z = (ŷ - y) × ŷ(1-ŷ)
当医生很自信时：

• ŷ接近0或1
• ŷ(1-ŷ)接近0
• 整个梯度接近0
• 学习停止！

交叉熵梯度：∂L/∂z = ŷ - y

当医生很自信时：

• ŷ接近0或1
• 但梯度仍然是ŷ-y
• 如果错了，梯度接近±1
• 继续学习！
  

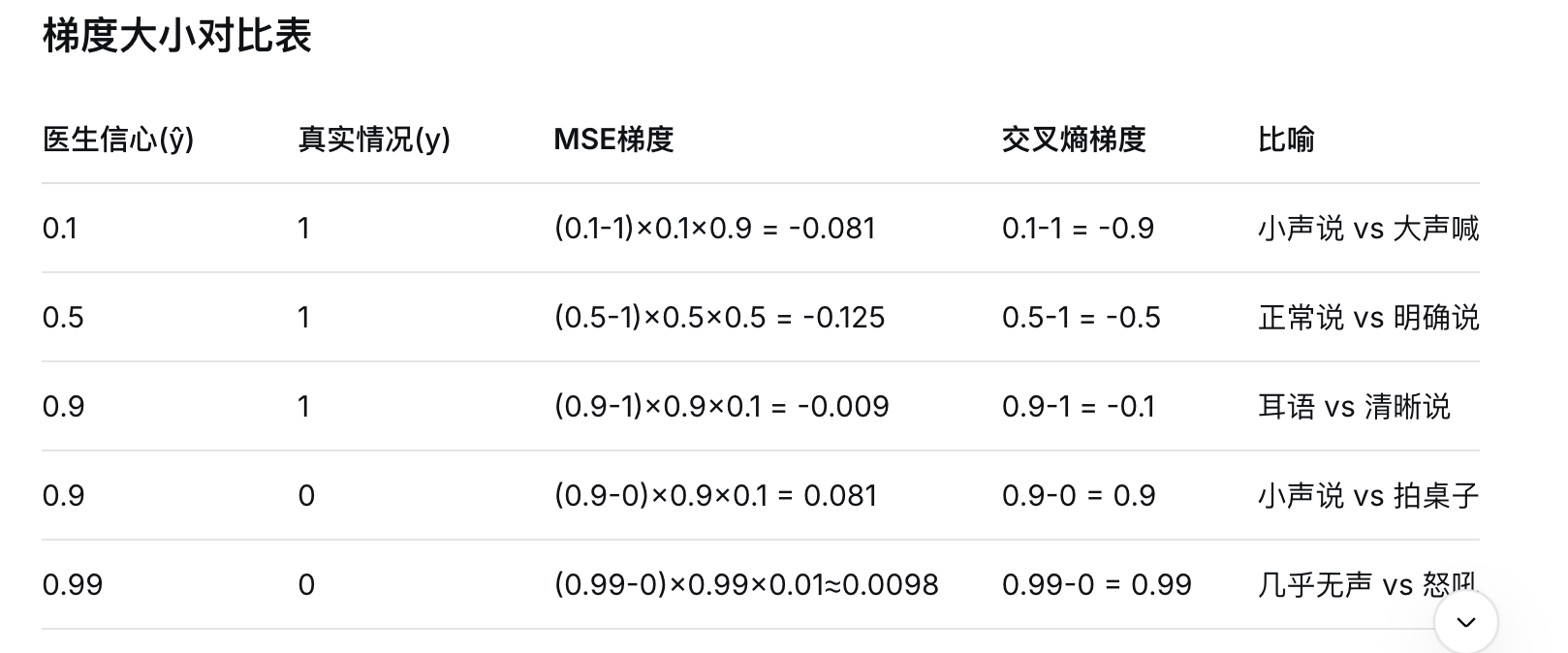
六.归一化和未归一化

1.归一化

归一化 = 把数据调整到标准范围内

你有3个苹果、2个香蕉、5个橙子
总数 = 3+2+5 = 10

归一化后：
苹果比例 = 3/10 = 0.3
香蕉比例 = 2/10 = 0.2  
橙子比例 = 5/10 = 0.5

总和正好等于1！

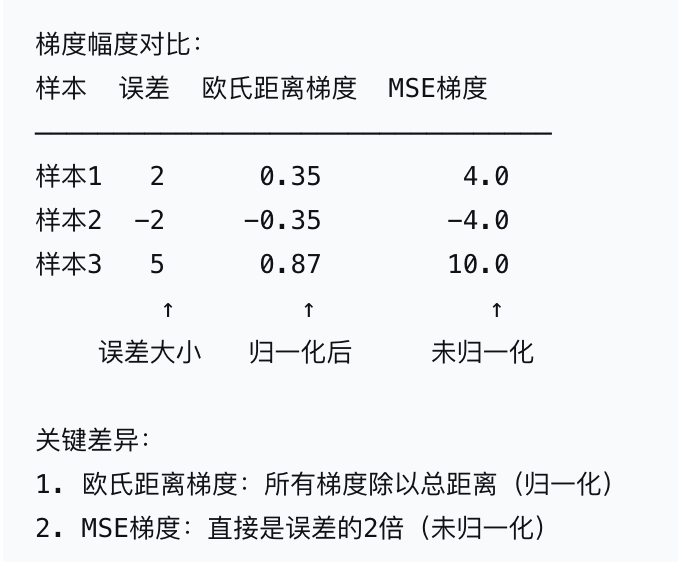
欧氏距离梯度就是归一化：
欧氏距离梯度公式：
梯度 = (预测误差) ÷ (总欧氏距离)

举个例子：
预测3个人的身高误差：
小明：误差 +2cm
小红：误差 -3cm
小刚：误差 +5cm

总欧氏距离 = √(2² + (-3)² + 5²) = √(4+9+25) = √38 ≈ 6.16

归一化后的梯度：
小明梯度 = 2 / 6.16 ≈ 0.32
小红梯度 = -3 / 6.16 ≈ -0.49
小刚梯度 = 5 / 6.16 ≈ 0.81

关键特点：所有梯度都在 -1 到 1 之间！

归一化的好处：

1. 公平比较
2. 加速训练
3. 防止梯度爆炸

2.未归一化

MSE梯度未归一化

3.对比