神经网络结构

1.人工神经元（M-P模型）

1.生物神经元的工作原理：

接收信号：树突接收来自其他神经元的化学信号。
整合信号：细胞体将所有输入信号进行汇总。
决策与输出：如果汇总的信号强度超过某个阈值，神经元就会被“激活”，通过轴突产生一个电脉冲输出给下一个神经元；否则，保持“静息”状态。

2.M-P模型将这个过程简化为三步数学操作：

1.加权求和：模拟信号整合。
每个输入 xᵢ 都对应一个权重 wᵢ。权重代表了该输入的重要性和影响方向。

wᵢ > 0：兴奋性连接，促进神经元激活。

wᵢ < 0：抑制性连接，阻止神经元激活。

|wᵢ| 的大小：连接强度。

神经元首先计算所有输入的加权和：
z = w₁x₁ + w₂x₂ + ... + wₙxₙ
这个 z 称为 净输入。
2.加上偏置：模拟内部阈值。
生物神经元有激活阈值。在M-P模型中，我们引入一个偏置 b。
z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
你可以把 b 理解为：

一个可调节的阈值：-b 就是实际阈值。

或者理解为，一个永远输入为 1 的特殊连接的权重。
激活函数：模拟“是否激活”的决策。

权重w和偏置b是通过训练得到的

"""
没有偏置项的神经元决策规则是：w₁x₁ + w₂x₂ = 0

这代表一条必须通过原点 (0,0) 的直线（在2D情况下）或一个必须通过原点的超平面（在高维情况下）。

问题：这极大地限制了分类能力。很多分类问题的分界线根本不过原点。

例子：我们要用一条直线把平面上的点分成两类。

没有偏置 b：你只能旋转通过原点的直线，像一把固定在原点的扇子。

有偏置 b：你可以把这条直线平移到平面的任何位置。b 就是控制这条直线上下/左右平移的参数。

所以，偏置 b 的作用是：为模型提供平移自由度，让决策边界（或拟合曲面）可以脱离原点，从而能够拟合更广泛的数据分布。
"""

3.激活函数（决策输出）
最后，净输入 z 被送入一个激活函数 f，产生最终输出 y：
y = f(z)

最早的M-P模型使用阶跃函数（又称单位阶跃函数）作为激活函数：

text
f(z) = { 1, 如果 z ≥ 0
{ 0, 如果 z < 0
意义：如果加权总和 z 达到或超过阈值（这里阈值是0，因为偏置 b 已包含在内），则神经元“激发”，输出1；否则，输出0。

3.详细计算举例：一个简单的“饥饿决策神经元”

假设我们构建一个神经元，用来决定是否要去吃午饭。它基于三个因素做决策：

输入 x₁：当前时间（12点=1，其他时间=0）。

输入 x₂：饥饿感（非常饿=1，不饿=0）。

输入 x₃：钱包有钱（有=1，无=0）。

神经元学习到的“经验”（权重和偏置）：

w₁ = 0.6：时间因素。权重为正，表示接近饭点是去吃饭的促进因素。

w₂ = 1.2：饥饿感。权重最大，表示这是最重要的因素。

w₃ = 0.4：钱包因素。权重为正，有钱才能去。

b = -1.0：偏置为负，可以理解为“惰性”或“基础阈值”。需要足够强的正面输入才能克服惰性。

激活函数：我们使用最简单的阶跃函数。f(z) = 1 (如果z≥0)，否则为0。输出 y=1 表示“去吃饭”，y=0 表示“不去”。
场景1：该去吃饭了（所有条件满足）
现在是12点，你很饿，钱包也有钱。
x₁ = 1, x₂ = 1, x₃ = 1

计算净输入 z：
z = w₁x₁ + w₂x₂ + w₃x₃ + b
z = (0.61) + (1.21) + (0.4*1) + (-1.0)
z = 0.6 + 1.2 + 0.4 - 1.0 = 1.2

通过激活函数：
y = f(z) = f(1.2)
因为 1.2 ≥ 0，所以 y = 1。

结论：神经元输出1，决定去吃饭。

场景2：不饿，但到饭点了
现在是12点，不饿，钱包有钱。
x₁ = 1, x₂ = 0, x₃ = 1

计算净输入 z：
z = (0.61) + (1.20) + (0.4*1) + (-1.0)
z = 0.6 + 0 + 0.4 - 1.0 = 0.0

通过激活函数：
y = f(0.0)
因为 0.0 ≥ 0，所以 y = 1。

结论：净输入刚好达到阈值，神经元仍输出1，决定去吃饭（可能是出于习惯）。

场景3：很饿，但没钱
不是12点，很饿，但没钱。
x₁ = 0, x₂ = 1, x₃ = 0

计算净输入 z：
z = (0.60) + (1.21) + (0.4*0) + (-1.0)
z = 0 + 1.2 + 0 - 1.0 = 0.2

通过激活函数：
y = f(0.2) = 1

结论：虽然没钱，但强烈的饥饿感克服了负偏置，仍决定去想办法吃饭。

场景4：不该去吃饭
不是12点，不饿，有钱。
x₁ = 0, x₂ = 0, x₃ = 1

计算净输入 z：
z = (0.60) + (1.20) + (0.4*1) + (-1.0)
z = 0 + 0 + 0.4 - 1.0 = -0.6

通过激活函数：
y = f(-0.6)
因为 -0.6 < 0，所以 y = 0。

结论：神经元输出0，决定不去吃饭。

4.几何意义：一个线性分类器

单个M-P神经元（使用阶跃激活函数）在几何上是一个线性分类器。

在我们“饥饿决策”的例子中，输入是三维的 (x₁, x₂, x₃)。神经元定义的规则是：
0.6x₁ + 1.2x₂ + 0.4x₃ - 1.0 ≥ 0 时，分为“去吃饭”类。

这是一个三维空间中的一个平面（决策边界）：

平面上方（z > 0）的点 → 输出1。

平面下方（z < 0）的点 → 输出0。

这就是单个神经元的能力极限：它只能学习用一条直线（2D）、一个平面（3D）或一个超平面（高维）将空间分成两类。 这就是为什么单层感知机无法解决“异或”等线性不可分问题。

2.sigmoid激活函数

1.核心特性：将任意实数“挤压”到(0,1)区间

Sigmoid函数，也叫逻辑函数，其公式为：

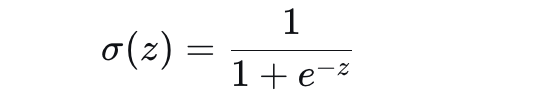
其中，e 是自然常数（约2.71828），z 是神经元的净输入（z = w·x + b）。

它的形状是一条光滑的S型曲线：

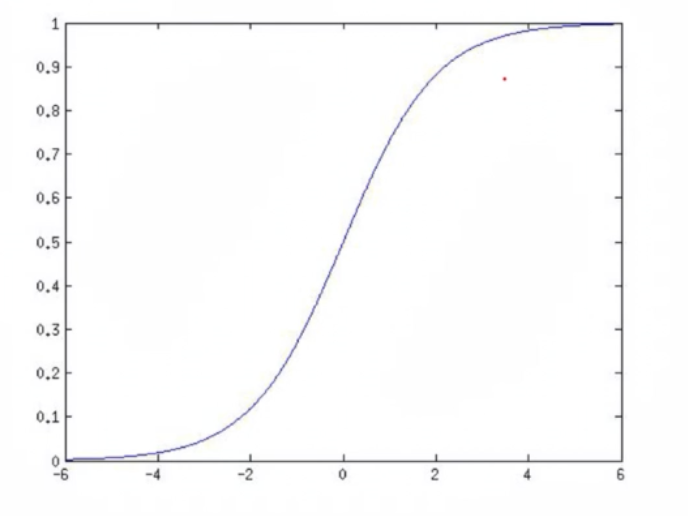
2.Sigmoid的导数（非常重要）

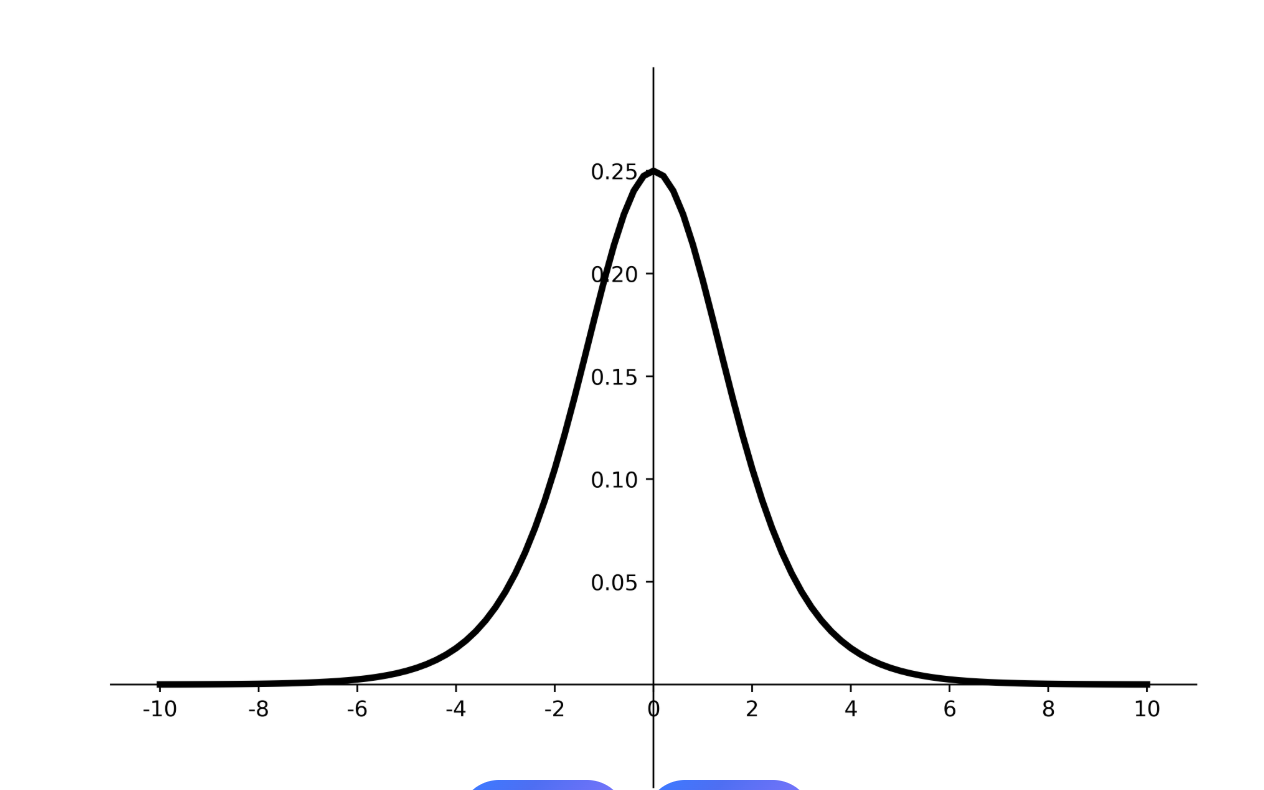
Sigmoid有一个非常优美的性质：它的导数可以用其自身表示

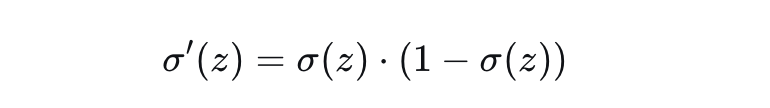
这意味着什么？

如果你已经计算出了神经元的输出 a = σ(z)，那么它的导数 σ'(z) 可以直接用 a*(1-a) 算出，无需重新计算复杂的指数函数，计算效率高。

导数的最大值出现在 z=0（此时 a=0.5），σ'(0) = 0.5*0.5 = 0.25。

当 z 很大或很小时（a接近0或1），导数趋近于0。这是导致梯度消失问题的根源。

4.梯度消失

梯度消失是指在训练深度神经网络（特别是RNN）时，用于更新网络权重的误差信号（梯度），在网络反向传播过程中，从输出层向输入层逐层传递时，会变得指数级地减小，最终趋近于零。这导致网络浅层的权重几乎得不到有效更新。就例如Sigmoid函数在趋近于正无穷和负无穷的时候，导数接近于0，就会出现梯度消失的问题。

5.详细计算举例

通过一个完整的例子，来看Sigmoid函数在神经元中是如何工作的。

场景：一个“考试通过预测”神经元
假设我们用一个神经元预测学生是否通过考试，基于两个特征：

x₁：学习小时数

x₂：模拟考分数

神经元已经训练好，参数为：
w₁ = 2.0, w₂ = 1.5, b = -3.0

激活函数：Sigmoid。输出 y 可以解释为“通过考试的概率”。

计算不同学生的预测概率：
学生A（努力型）：学习时间长，但模拟考一般。
x₁ = 1.0, x₂ = 0.2

计算净输入 z：
z = w₁x₁ + w₂x₂ + b = 2.01.0 + 1.50.2 + (-3.0) = 2.0 + 0.3 - 3.0 = -0.7

应用Sigmoid函数：
σ(z) = 1 / (1 + e^{-z}) = 1 / (1 + e^{0.7}) （注意：e^{-(-0.7)} = e^{0.7}）
计算 e^{0.7} ≈ 2.0138
所以 σ(-0.7) = 1 / (1 + 2.0138) = 1 / 3.0138 ≈ 0.332

结论：学生A的通过概率约为 33.2%。

学生B（天赋型）：学习时间短，但模拟考高分。
x₁ = 0.3, x₂ = 1.0

计算净输入 z：
z = 2.00.3 + 1.51.0 - 3.0 = 0.6 + 1.5 - 3.0 = -0.9

应用Sigmoid函数：
σ(-0.9) = 1 / (1 + e^{0.9})
e^{0.9} ≈ 2.4596
σ(-0.9) = 1 / (1 + 2.4596) = 1 / 3.4596 ≈ 0.289

结论：学生B的通过概率约为 28.9%。

学生C（全面型）：学习时间长，模拟考也高分。
x₁ = 0.8, x₂ = 0.9

计算净输入 z：
z = 2.00.8 + 1.50.9 - 3.0 = 1.6 + 1.35 - 3.0 = -0.05

应用Sigmoid函数：
σ(-0.05) = 1 / (1 + e^{0.05})
e^{0.05} ≈ 1.0513
σ(-0.05) = 1 / (1 + 1.0513) = 1 / 2.0513 ≈ 0.487

结论：学生C的通过概率约为 48.7%。

观察：净输入 z 从-0.9 → -0.7 → -0.05 逐渐增加，对应的Sigmoid输出（概率）也从 28.9% → 33.2% → 48.7% 平滑增加，符合我们的直觉。

tanh激活函数

tanh函数图像和其导数图像

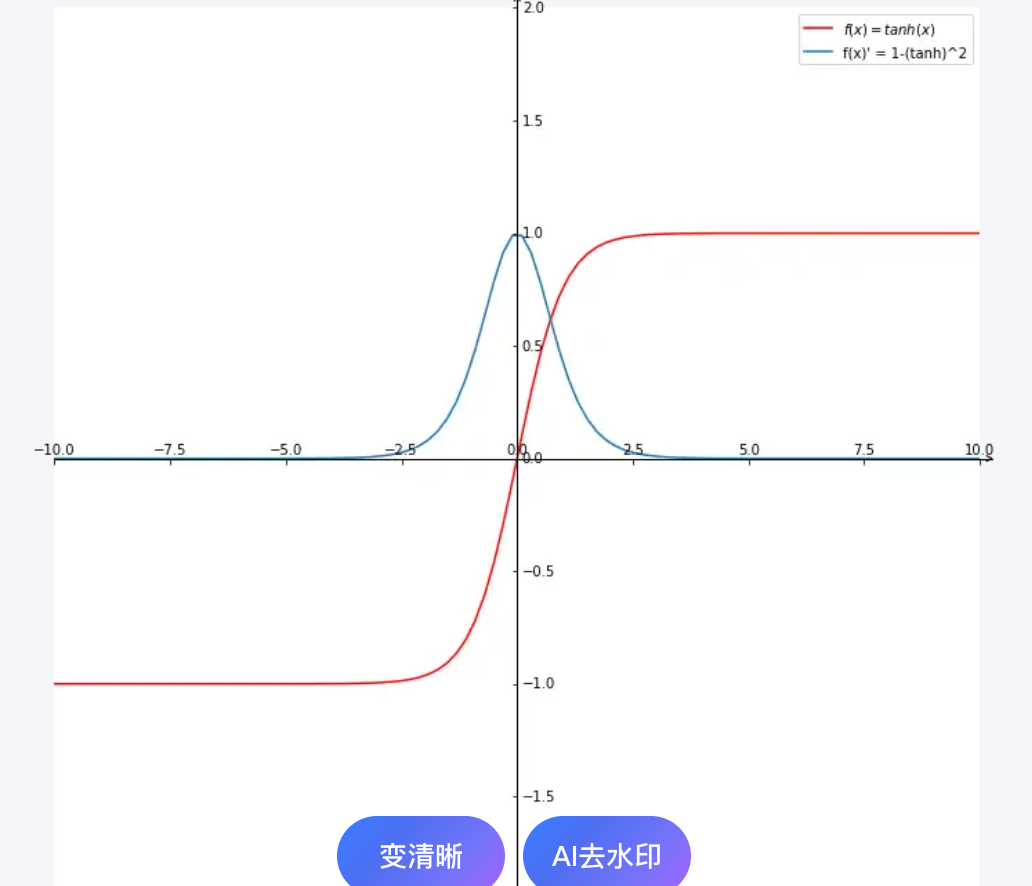
tanh函数比sigmoid图像的优点：
Sigmoid的输出始终为正：它的输出范围是(0, 1)，这意味着所有神经元的激活值都是正数。
Tanh的输出以零为中心：它的输出范围是(-1, 1)，平均值为0。

Tanh的输出有正有负，可以提供更丰富的梯度方向，使得权重更新路径更直接，收敛速度通常更快、更稳定。

3.神经网络结构

1.描述

想象一个汽车制造厂：

输入层：原始材料（钢材、玻璃、轮胎）。

隐藏层：不同的生产车间。

第一车间：冲压钢板，制造车身框架。

第二车间：安装发动机和传动系统。

第三车间：安装内饰和电子设备。

输出层：成品汽车。

每个车间（神经元）都对来自上游的材料（数据）进行加工，然后传递给下一个车间。神经网络就是这样一个将原始输入数据，通过多层非线性变换，逐步加工成最终输出（预测）的系统。

输入层的维度是固定的，等于你的特征数量。

二、神经网络的基本结构详解

一个标准的神经网络（前馈神经网络）由三部分组成：

1. 输入层
   作用：接收原始数据。它不对数据进行任何计算，只是将数据“喂入”网络。

神经元数量：等于输入特征的维度。

示例：要预测房价，特征可能是 [面积, 卧室数, 房龄]，那么输入层就有3个神经元。

2. 隐藏层
   作用：核心计算层。在这里进行特征的提取、组合和抽象。可以有一层或多层。

“隐藏”的含义：这些层的输出不直接作为最终预测结果，也不直接面向原始输入，它们的值在训练过程中是“隐藏”的、内部抽象的。

每层的计算：每个隐藏层神经元执行两个操作：

加权求和：z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

非线性激活：a = f(z)，如ReLU, Sigmoid

深度：隐藏层的数量决定了网络的“深度”。层数越多，能学习的特征越抽象、越复杂。

3. 输出层
   作用：产生最终预测。

神经元数量和激活函数取决于任务类型：

回归任务（预测连续值）：1个神经元，通常不使用激活函数（或使用线性激活）。

二分类任务：1个神经元，使用Sigmoid激活函数（输出概率）。

多分类任务：神经元数=类别数，使用Softmax激活函数（输出概率分布）。

三、详细举例说明：一个房价预测神经网络

假设我们要预测房价，有3个特征：

x₁：面积（平方米）

x₂：卧室数量

x₃：房龄（年）

我们设计一个 2层隐藏层 的神经网络，结构如下：

输入层：3个神经元（对应3个特征）

隐藏层1：4个神经元

隐藏层2：2个神经元

输出层：1个神经元（预测房价，回归任务）

第一步：输入层 → 隐藏层1
输入数据：X = [x₁, x₂, x₃]（例如 [100, 3, 10]）
隐藏层1有4个神经元，每个神经元有3个权重和1个偏置。

以第一个神经元为例：
z₁^{[1]} = w₁₁^{[1]}x₁ + w₁₂^{[1]}x₂ + w₁₃^{[1]}*x₃ + b₁^{[1]}
然后应用ReLU激活函数：
a₁^{[1]} = ReLU(z₁^{[1]})

对4个神经元都进行此计算，得到隐藏层1的输出向量：
A^{[1]} = [a₁^{[1]}, a₂^{[1]}, a₃^{[1]}, a₄^{[1]}]
注意：A^{[1]} 不再是原始特征，而是原始特征的第一次非线性组合抽象，可以理解为“初级特征”。

第二步：隐藏层1 → 隐藏层2
隐藏层2有2个神经元，每个神经元接收来自上一层4个神经元的输入。

以隐藏层2的第一个神经元为例：
z₁^{[2]} = w₁₁^{[2]}*a₁ + w₁₂^{[2]}*a₂ + w₁₃^{[2]}*a₃ + w₁₄^{[2]}*a₄ + b₁^{[2]}
a₁^{[2]} = ReLU(z₁^{[2]})
得到隐藏层2的输出向量：
A^{[2]} = [a₁^{[2]}, a₂^{[2]}]
这是更高级、更抽象的特征。

第三步：隐藏层2 → 输出层
输出层只有1个神经元，进行回归预测。
z^{[3]} = w₁₁^{[3]}*a₁ + w₁₂^{[3]}*a₂ + b^{[3]}
因为是回归任务，输出层通常不使用激活函数（或用恒等函数）：
ŷ = z^{[3]}

这个 ŷ 就是神经网络预测的房价。

四.神经网络的本质

神经网络本质就是一个多层复合函数
通过调整权重和偏置项实现不同的映射
权重和偏置项是通过训练得到的

4.正向传播算法

想象一排排列好的多米诺骨牌：
你推倒第一块（输入数据）
第一块撞倒第二块（第一层计算）
第二块撞倒第三块（第二层计算）
...直到最后一块倒下（得到输出）

一.正向传播的数学本质

正向传播要做的事情非常简单：
对于网络中的每一层，重复以下两步：
z = W · a_prev + b （线性变换）
a = f(z) （非线性激活）
其中：
W：权重矩阵
a_prev：上一层的激活值（对第一层来说就是输入 X）
b：偏置向量
f：激活函数
a：当前层的输出（激活值）

二. 详细计算示例：手写数字识别

我们用一个简单的3层网络（1层隐藏层）来识别手写数字"8"。

网络架构：
text
输入层：4个神经元（简化版，实际是784个）
隐藏层：3个神经元，使用Sigmoid激活
输出层：2个神经元（二分类：是8/不是8），使用Sigmoid激活

第一层权重 W¹（连接输入层和隐藏层）：

W¹ = [[ 0.1, -0.2,  0.3,  0.4],   # 隐藏层神经元1的权重
      [-0.5,  0.6, -0.7,  0.8],   # 隐藏层神经元2的权重  
      [ 0.9, -1.0,  1.1, -1.2]]   # 隐藏层神经元3的权重
形状：(3, 4)  # 3个目标神经元 × 4个源神经元

第一层偏置 b¹：

b¹ = [[0.1],
      [0.2],
      [0.3]]
形状：(3, 1)

第二层权重 W²（连接隐藏层和输出层）：

W² = [[ 1.1, -1.2,  1.3],   # 输出层神经元1的权重
      [-1.4,  1.5, -1.6]]   # 输出层神经元2的权重
形状：(2, 3)

第二层偏置 b²：

b² = [[0.4],
      [0.5]]
形状：(2, 1)

输入数据：
假设数字"8"的简化特征向量为：

X = [[0.8],   # 特征1：有顶部弧线
     [0.2],   # 特征2：有右侧垂直线
     [0.9],   # 特征3：有底部弧线  
     [0.1]]   # 特征4：有左侧垂直线
形状：(4, 1)

运算：
第一步：输入层 → 隐藏层

1. 线性变换：

z¹ = W¹ · X + b¹

计算过程：

z¹ = [[ 0.1*0.8 + (-0.2)*0.2 + 0.3*0.9 + 0.4*0.1 + 0.1],
      [(-0.5)*0.8 + 0.6*0.2 + (-0.7)*0.9 + 0.8*0.1 + 0.2],
      [ 0.9*0.8 + (-1.0)*0.2 + 1.1*0.9 + (-1.2)*0.1 + 0.3]]
    
  = [[ 0.08 - 0.04 + 0.27 + 0.04 + 0.1],
      [-0.40 + 0.12 - 0.63 + 0.08 + 0.2],
      [ 0.72 - 0.20 + 0.99 - 0.12 + 0.3]]
    
  = [[0.45],
      [-0.63],
      [1.69]]

2. 非线性激活（使用Sigmoid）：
   a¹ = σ(z¹) = 1 / (1 + e^{-z¹})

a¹ = [[1 / (1 + e^{-0.45})],
      [1 / (1 + e^{0.63})],    # 注意：e^{-(-0.63)} = e^{0.63}
      [1 / (1 + e^{-1.69})]]
    
  = [[1 / (1 + 0.6376)],   # e^{-0.45} ≈ 0.6376
      [1 / (1 + 1.8776)],   # e^{0.63} ≈ 1.8776  
      [1 / (1 + 0.1842)]]   # e^{-1.69} ≈ 0.1842
    
  = [[0.610],
      [0.347],
      [0.844]]

隐藏层的输出：a¹ = [[0.610], [0.347], [0.844]]
这个向量可以理解为：隐藏层从原始像素特征中提取出的3个抽象特征。

第二步：隐藏层 → 输出层
第一步：输入层 → 隐藏层

1. 线性变换：

z¹ = W¹ · X + b¹

计算过程：

z² = [[ 1.1*0.610 + (-1.2)*0.347 + 1.3*0.844 + 0.4],
      [(-1.4)*0.610 + 1.5*0.347 + (-1.6)*0.844 + 0.5]]
    
  = [[ 0.671 - 0.416 + 1.097 + 0.4],
      [-0.854 + 0.521 - 1.350 + 0.5]]
    
  = [[1.752],
      [-1.183]]

2.非线性激活（使用Sigmoid）：

ŷ = σ(z²) = a² = [[1 / (1 + e^{-1.752})],
                  [1 / (1 + e^{1.183})]]   # e^{-(-1.183)} = e^{1.183}
    
  = [[1 / (1 + 0.1736)],   # e^{-1.752} ≈ 0.1736
      [1 / (1 + 3.264)]]   # e^{1.183} ≈ 3.264
    
  = [[0.852],
      [0.234]]

最终输出：
ŷ = [[0.852], [0.234]]

结果解释与决策
输出层有两个神经元：

神经元1：输出 0.852 → 表示模型认为是数字"8"的概率为85.2%

神经元2：输出 0.234 → 表示模型认为不是数字"8"的概率为23.4%

注意：这两个概率相加不等于1，因为两个神经元是独立的（使用Sigmoid激活）。如果希望概率和为1，应该使用Softmax激活。

决策规则：
如果设定阈值为0.5
0.852 > 0.5 且 0.234 < 0.5
所以模型预测：这是数字"8"

5.分类问题和回归问题

从概率视角看
分类：模型输出是类别的概率分布。
例如：图片是“猫”的概率=0.85，是“狗”的概率=0.15。
最终预测取概率最大的类别：\(\hat{y} = \arg\max_{c} P(y=c|x)\)

回归：模型输出是条件期望值。
例如：给定房屋特征，预测其价格=\(352,000。 通常假设误差服从正态分布：\)y \sim \mathcal{N}(f(x), \sigma^2)$

输出空间的不同：
分类：输出空间是有限的、离散的集合。
例如：{猫, 狗, 鸟}，{是, 否}，{0, 1, 2, 3, 4}
即使输出是概率（0到1之间的连续值），最终决策仍然是离散的类别

回归：输出空间是连续的实数区间。
例如：房价（$200,000到$2,000,000之间的任意值），温度（-10.5°C到42.3°C）
预测值可以是无限精度的数值

现实世界的例子
分类问题示例：
垃圾邮件检测：{垃圾邮件，正常邮件}

疾病诊断：{患病，健康}

图像识别：{猫，狗，汽车，飞机...}

情感分析：{正面，负面，中性}

风险评估：{高风险，中风险，低风险}

回归问题示例：
房价预测：预测具体价格（$352,478）

股价预测：预测明日收盘价

温度预测：预测明天最高气温（23.7°C）

销量预测：预测下个月产品销量（1,245件）

年龄预测：从照片预测人的年龄（估计为32.5岁）