Lecture8 Neural NetWork：Representation

Lecture8 Neural NetWork：Representation

Non-linear hypotheses

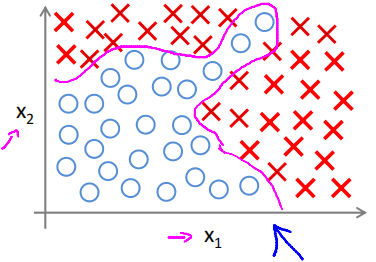
Neural NetWork

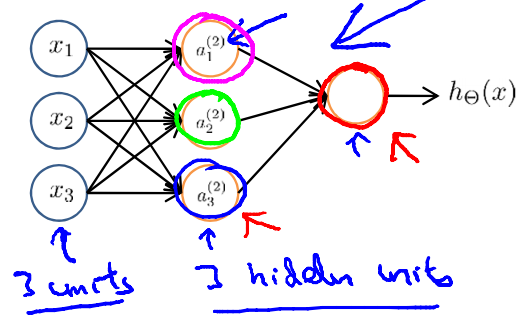
\(a_i^{(j)}\) = "activation" of unit i in layer j

\(\Theta^{(j)}\) = matrix of weights controlling function mapping from layer \(j\) to layer \(j+1\)

\[\begin{align} a_1^{(2)} & = g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2+\Theta_{13}^{(1)}x_3) \\ a_2^{(2)} & = g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}^{(1)}x_2+\Theta_{23}^{(1)}x_3) \\ a_1^{(3)} & = g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}^{(1)}x_2+\Theta_{33}^{(1)}x_3) \\ h_\Theta(x) & = a_1^{(3)}=g(\Theta_{10}^{(2)}a_0^{(2)}+\Theta_{11}^{(2)}a_1^{(2)}+\Theta_{12}^{(2)}a_2^{(2)}+\Theta_{13}^{(2)}a_3^{(2)}) \end{align} \]

if network has \(s_j\) units in layer j,\(s_{j+1}\) units in layer j+1,then \(\Theta^{(j)}\) will be of dimension \(s_{j+1} \times (s_j+1)\)

Vectorized implementation

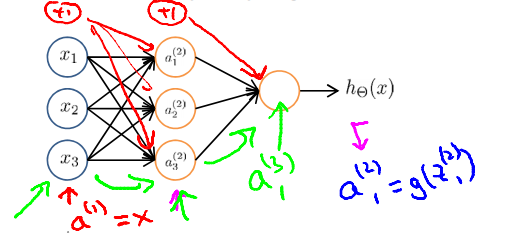
\[x = \left[\begin{matrix} x_0 \\ x_1 \\ x_3 \\ x_4 \\ \end{matrix}\right] \ z^{(2)} = \left[\begin{matrix} z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(2)} \end{matrix}\right] \\ z^{(2)} = \Theta^{(1)}a^{(1)} \\ a^{(2)} = g(z^{(2)}) \\ Add\ a_0^{(2)} = 1 \Rightarrow a^{(2)} \in \mathbb{R}^4\\ z^{(3)} = \Theta^{(2)})a^{(2)} \\ h_\Theta(x) = a^{(3)} = g(z^{(3)}) \]

Examples and intuitions

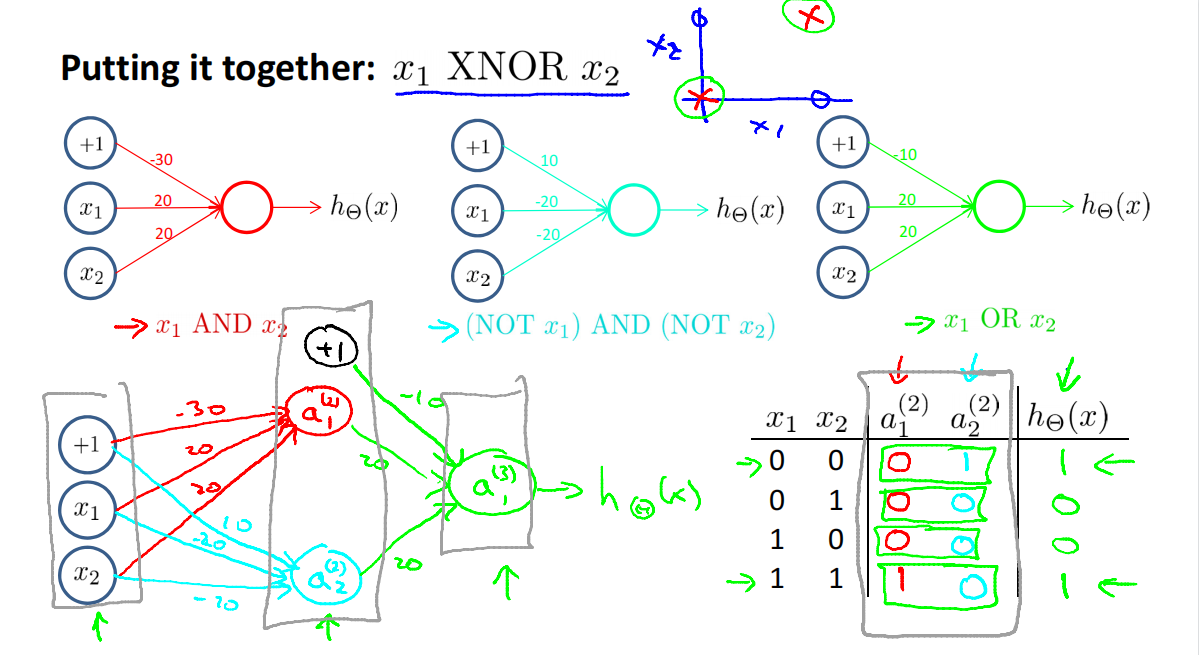
Non-linear classification example: XOR/XNOR

Simple example: AND

\(x_1,x_3 \in {0,1}\)

\(y = x1\ AND\ x_2\)

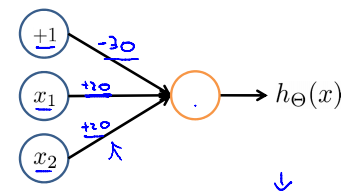
\[\Theta_{10} = -30 \\ \Theta_{11} = 20 \\ \Theta_{11} = 20 \\ h_\Theta(x) = g(-30 + 20x_1+20x_2) \]

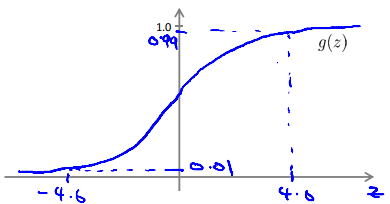
\(x_1\)	\(x_2\)	\(h_\Theta(x)\)
0	0	\(g(-30)\approx0\)
0	1	\(g(-10)\approx0\)
1	0	\(g(-10)\approx0\)
1	1	\(g(10)\approx0\)

Example: OR function

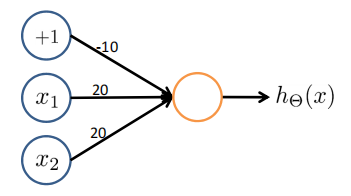
\[h_\Theta(x) = g(-10+20x_1+20x_2) \]

\(x_1\)	\(x_2\)	\(h_\Theta(x)\)
0	0	\(g(-10)\approx0\)
0	1	\(g(10)\approx1\)
1	0	\(g(10)\approx1\)
1	1	\(g(30)\approx1\)

Negation

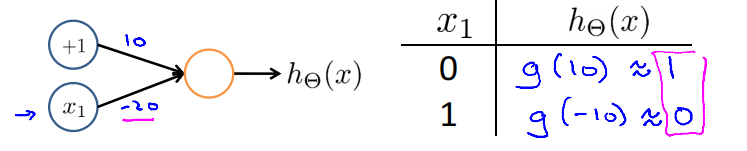
XOR