[NOI2020]又是自闭的两天。。。。

别问，问多了都是泪

目录

 

D1T1.美食家

刚做完看到群里都在说是矩阵乘法的我？？？

回头看了眼题目和数据瞬间崩溃，五十个城市，第T天，就差把矩阵乘法扣我脸上了（可惜我瞎）

不熟悉矩阵乘法优化图论题的可以先做做这道 POJ3613

考虑怎么把这道题靠到这道板子题上

查看数据发现边权很小（w<=5),可以拆点，对于每一个城市，除了第w-1个点和第w个点的边权保留原值之外，其他都设为0

然后就是矩阵乘法的常规操作

但是还有一个节日的因素，其实这个不会造成很大改动，只需要在两个相邻的节日间用矩阵乘法，然后再城市上加上权值就可以了。然后初始化的时候要加两个自设的节日（0，0，0），（T，0，0）

具体见代码

  1 #include<bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 const int MAXN=55;
  6 const int MAXK=205;
  7 const int INF=1e9;
  8 
  9 typedef long long LL;
 10 
 11 int N,M,T,K,tot;
 12 int c[MAXN];
 13 int p[MAXN][6];
 14 struct node{
 15     int t,x,y;
 16     node(){}
 17     node(int _t,int _x,int _y){
 18         t=_t;
 19         x=_x;
 20         y=_y;
 21     }
 22     bool operator < (const node &b) const{
 23         return t<b.t;
 24     }
 25 }f[MAXK];
 26 
 27 struct Matrix{
 28     LL dis[MAXN*5][MAXN*5];
 29 }a[35],unit;
 30 
 31 struct ANS{
 32     LL dis[MAXN*5];
 33 }ans;
 34 
 35 Matrix MUL1(Matrix a,Matrix b){
 36     Matrix c=unit;
 37     for(int i=1;i<=tot;i++){
 38         for(int j=1;j<=tot;j++)if(a.dis[i][j]>=0){
 39             for(int k=1;k<=tot;k++){
 40                 c.dis[i][k]=max(c.dis[i][k],a.dis[i][j]+b.dis[j][k]);
 41             } 
 42         }
 43     }
 44     return c;
 45 }
 46 
 47 void init(){
 48     for(int i=1;i<=tot;i++){
 49         for(int j=1;j<=tot;j++) unit.dis[i][j]=-INF;
 50     } 
 51     sort(f+1,f+1+K);
 52     f[0]=node(0,0,0);
 53     f[K+1]=node(T,0,0);
 54     for(int i=1;i<=30;i++){
 55         a[i]=MUL1(a[i-1],a[i-1]);
 56     }
 57 //    cout<<a[2].dis[1][3]<<endl;
 58     for(int i=1;i<=tot;i++) ans.dis[i]=-INF;
 59     ans.dis[1]=c[1];
 60 }
 61 
 62 ANS MUL2(ANS a,Matrix b){
 63     ANS tmp;
 64     for(int i=1;i<=tot;i++) tmp.dis[i]=-INF;
 65     for(int i=1;i<=tot;i++)if(a.dis[i]>=0){
 66         for(int j=1;j<=tot;j++)if(b.dis[i][j]>=0){
 67             tmp.dis[j]=max(tmp.dis[j],a.dis[i]+b.dis[i][j]);
 68         }
 69     }
 70     return tmp;
 71 }
 72 
 73 void qpow(int b){
 74     for(int i=0;i<=30;i++)if((1<<i)&b){
 75         ans=MUL2(ans,a[i]);
 76 //        for(int i=1;i<=N;i++) printf("%lld\n",ans.dis[i]);
 77     }
 78 }
 79 
 80 int main(){
 81     scanf("%d%d%d%d",&N,&M,&T,&K);
 82     for(int i=1;i<=N;i++) scanf("%d",&c[i]);
 83     tot=N;
 84     for(int i=1;i<=N;i++) p[i][0]=i;
 85     for(int i=1;i<=N*5;i++){
 86         for(int j=1;j<=N*5;j++) a[0].dis[i][j]=-INF;
 87     }
 88     for(int i=1,u,v,w;i<=M;i++){
 89         scanf("%d%d%d",&u,&v,&w);
 90         for(int j=1;j<w;j++)if(!p[u][j]) p[u][j]=++tot;
 91         for(int j=1;j<w;j++) a[0].dis[p[u][j-1]][p[u][j]]=0;
 92         a[0].dis[p[u][w-1]][v]=c[v];
 93     }
 94 //    cout<<tot<<endl;
 95     for(int i=1,t,x,y;i<=K;i++){
 96         scanf("%d%d%d",&t,&x,&y);
 97         f[i]=node(t,x,y);
 98     }
 99     init();
100     for(int i=1;i<=K+1;i++){
101         int t=f[i].t-f[i-1].t;
102 //        cout<<t<<endl;
103         qpow(t);
104         ans.dis[f[i].x]+=f[i].y;
105 //        for(int i=1;i<=N;i++) cout<<ans.dis[i]<<endl;
106     }
107     if(ans.dis[1]<0) printf("-1");
108     else printf("%lld",ans.dis[1]); 
109     return 0;
110 }
View Code

 

D1T2.命运

 

 有看到大佬说这道题是水题，个人觉得这题是两天前两道里最难搞懂的一题

首先看题面，存在多少种不同的方案确定每条边是否是重要的，不难联想到容斥。强制让若干条链不满足，贡献就是链上的边只能取0，其余边的值可以随便取的方案数，容斥系数为 (−1)^k，其中k为选择的不满足链数量。

 

这里有一个优化，就是对于每一条终点为v的链，我们只用考虑起点深度最大的链，因为只要这条链满足了，那么终点为v的所有链都会满足，反之必然会存在至少一条链不满足，不需计入答案

令 dp[i][j]​ 表示以i为根的子树,从根节点到深度为j的祖先路径上的每条边都要赋值为0的方案数。

转移为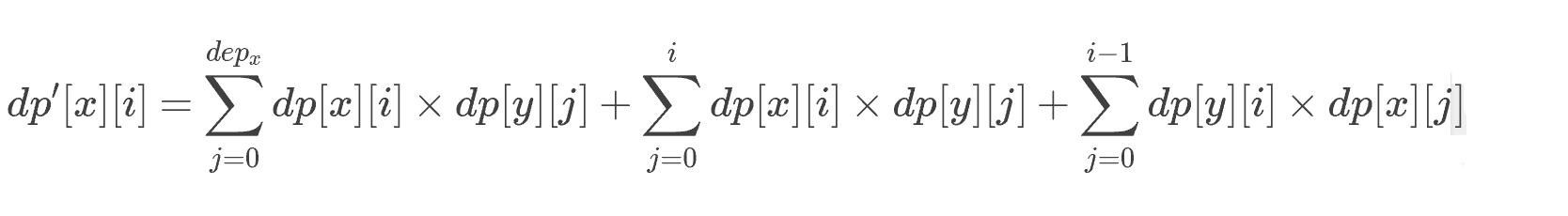：（原谅我不知道怎么打公式）

 

注意那个dp[y][j]要先乘个2，表示x->y这条边可随意选

注意到若只有n条链的下端点位于i的子树中,则dp[i][j]除0之外只有 O(n)种取值。用线段树维护，每次操作的时候进行线段树合并，先走左子树再走右子树，走左子树的时候带上右子树的值

具体见代码

#include<bits/stdc++.h>

using namespace std;

const int MAXN=5e5+5;
const int MOD=998244353;
typedef long long LL;

int N,M,cnt=0,tot=0;
struct node{
    int to,nxt;
}edge[MAXN<<1];
int head[MAXN],dep[MAXN],en[MAXN],rt[MAXN];

struct TREE{
    int l,r;
    LL sum,lazy;
}tr[MAXN*40];

void add(int u,int v){
    edge[cnt].to=v;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}

void dfs(int u,int pre){
    dep[u]=dep[pre]+1;
    for(int i=head[u];i!=-1;i=edge[i].nxt){
        int v=edge[i].to;
        if(v==pre) continue;
        dfs(v,u);
    }
}

void init(){
    memset(head,-1,sizeof(head));
    memset(en,0,sizeof(en));
}

void update(int &root,int l,int r,int pos,int w){
    if(!root){
        root=++tot;
        tr[root].lazy=1;
        tr[root].sum=0;
    }
    tr[root].sum=(tr[root].sum+w)%MOD;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(pos<=mid) update(tr[root].l,l,mid,pos,w);
    else update(tr[root].r,mid+1,r,pos,w);
}

void pushdown(int root){
    if(tr[root].lazy==1) return;
    tr[tr[root].l].lazy=tr[tr[root].l].lazy*tr[root].lazy%MOD;
    tr[tr[root].l].sum=tr[tr[root].l].sum*tr[root].lazy%MOD;
    tr[tr[root].r].lazy=tr[tr[root].r].lazy*tr[root].lazy%MOD;
    tr[tr[root].r].sum=tr[tr[root].r].sum*tr[root].lazy%MOD;
    tr[root].lazy=1;
}

void pushup(int root){
    tr[root].sum=(tr[tr[root].l].sum+tr[tr[root].r].sum)%MOD;
}

void mul(int root,int l,int r,int L,int R){
    if(!root) return;
    if(l>=L&&r<=R){
        tr[root].lazy=tr[root].lazy*2%MOD;
        tr[root].sum=tr[root].sum*2%MOD;
//        cout<<root<<" "<<tr[root].sum<<endl;
        return;
    }
    pushdown(root);
    int mid=(l+r)>>1;
    if(L<=mid) mul(tr[root].l,l,mid,L,R);
    if(R>mid) mul(tr[root].r,mid+1,r,L,R);
    pushup(root);
}

int Merge(int rt1,int rt2,int l,int r,LL s1,LL s2){
    if(!rt1||!rt2){
        tr[rt1].lazy=tr[rt1].lazy*s2%MOD;
        tr[rt1].sum=tr[rt1].sum*s2%MOD;
        tr[rt2].lazy=tr[rt2].lazy*s1%MOD;
        tr[rt2].sum=tr[rt2].sum*s1%MOD;
        return rt1^rt2;
    }
    if(l==r){
        tr[rt1].sum=(tr[rt1].sum*s2%MOD+tr[rt2].sum*s1%MOD+tr[rt1].sum*tr[rt2].sum%MOD)%MOD;
//        cout<<rt1<<" "<<tr[rt1].sum<<endl;
        return rt1;
    }
    pushdown(rt1);
    pushdown(rt2);
    int mid=(l+r)>>1;
    tr[rt1].l=Merge(tr[rt1].l,tr[rt2].l,l,mid,(s1+tr[tr[rt1].r].sum)%MOD,(s2+tr[tr[rt2].r].sum)%MOD);
    tr[rt1].r=Merge(tr[rt1].r,tr[rt2].r,mid+1,r,s1,s2);
    pushup(rt1);
//    cout<<rt1<<" "<<tr[rt1].sum<<" "<<tr[rt1].l<<" "<<tr[rt1].r<<endl;
    return rt1;
}

void solve(int u,int pre){
    if(en[u]) update(rt[u],1,N,en[u],MOD-1);//选一条边，初始-1
    update(rt[u],1,N,N,1); 
    for(int i=head[u];i!=-1;i=edge[i].nxt){
        int v=edge[i].to;
        if(v==pre) continue;
        solve(v,u);
        mul(rt[v],1,N,dep[v],N);//u->v这条边可取0可取1
        rt[u]=Merge(rt[u],rt[v],1,N,0,0); 
//        cout<<rt[u]<<endl;
    }
}

int main(){
    init();
    scanf("%d",&N);
    for(int i=1,u,v;i<N;i++){
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    dfs(1,0);
    scanf("%d",&M);
    for(int i=1,u,v;i<=M;i++){
        scanf("%d%d",&u,&v);
        en[v]=max(en[v],dep[u]);//考虑对于同一个点，只有最近的一个点（深度最大）会影响答案，因为假如最近的这条边满足了
        //剩下的几条更长的便肯定满足，但是如果最短的边不满足，那么就不记录答案 
    }
//    for(int i=1;i<=N;i++) cout<<en[i]<<endl;
    solve(1,0);
//    for(int i=1;i<=N;i++) cout<<rt[i]<<endl;
    printf("%lld",tr[rt[1]].sum); 
    return 0;
}
View Code

 

D2T1.制作菜品

我分了三种情况考虑，但是我的做法跑得贼慢，可能是我写得太烂了。

第一种：M>=N

首先量等于K的食材我们可以直接计入答案。那就只剩量小于K和量大于K的食材

针对每一个量小于K，我们一定可以找到一个量大于K的食材，合并成一个等于K的菜品。而那个量原先大于K的食材会遇到三种情况

  •  合并后量恰好为K，直接计入答案

  •  合并后量仍大于K，放回去，再重新找到一个量小于K的食材，重复上述步骤

  •  合并后量小于K，直接重复上述步骤

 

直到找不到量小于K的食材，结束。因为N==M且总量==N*K，所以一定是有解的。

则对于M>N，只需要初始化的时候放入M-N个量为0的食材，注意计入答案的时候要判一下（不然只有35分。。。）

 

第二种：M==N-1

先考虑取出一个量大于K的食材，则转换成第一种情况，然后肯定会剩一些量小于K的食材，然后用原来取出的那个食材去补，一定有解

 

第三种：M==N-2

直接考虑这种情况不好想，所以我们还是先考虑把他拆成两个M==N-1的集合。

如果能拆成这样两个集合，那一定是有解的，和第二种情况相同

那我们现在需要证明的只有当不满足这个条件的时候，一定没有解。

我们假设每两个组成一道菜品的食材连一条边，则至多有N-2条边，一定不联通，设这张图有一个连通块，则这个连通块一定满足M==N-1这个条件，证毕。

所以现在只需要判断有没有解，再转换成第二种情况就可以了。判断直接01背包bitset优化即可

具体见代码

 

#include<bits/stdc++.h>

using namespace std;

const int MAXM=5e3+5;

int T,N,M,K,num;
int d[MAXM],tmp[MAXM];
bitset<5000005> dp[505];
int vis[MAXM];

struct node{
    int id1,id2;
    int d1,d2;
    node(){}
    node(int a,int b,int c,int _d){
        id1=a;
        d1=b;
        id2=c;
        d2=_d;
    }
}ans[MAXM];

queue<int>q1,q2;

void clear(){
    while(!q1.empty()) q1.pop();
    while(!q2.empty()) q2.pop();
}

void print(){
    for(int i=1;i<=M;i++){
        printf("%d %d",ans[i].id1,ans[i].d1);
        if(ans[i].id2) printf(" %d %d",ans[i].id2,ans[i].d2);
        printf("\n");
    }
}

void solve1(){
    for(int i=1;i<=N;i++){
        if(d[i]==K){
            ans[++num]=node(i,K,0,0);
        }else if(d[i]<K)q1.push(i);
        else q2.push(i);
    } 
    for(int i=N+1;i<=M;i++) q1.push(i);
    while(!q1.empty()){
        int u=q1.front();
        q1.pop(); 
        while(d[u]<K){
            int v=q2.front();
            q2.pop();
            if(!d[u]) ans[++num]=node(v,K,0,0); 
            else ans[++num]=node(u,d[u],v,K-d[u]);
            d[v]-=K-d[u];
            u=v;
        } 
        if(d[u]==K){
            ans[++num]=node(u,d[u],0,0);
        }else q2.push(u);
    }
    clear(); 
    print();
}

void work(int n,int m){
    int pos;
    for(int i=n;i>=1;i--){
        if(d[i]!=0){
            pos=i;
            break;
        }
    }
    for(int i=1;i<=pos-1;i++){
        if(d[i]==K){
            ans[++num]=node(i,K,0,0);
        }else if(!d[i]) continue;
        else if(d[i]<K) q1.push(i);
        else q2.push(i);
    }
    while(!q1.empty()){
        if(q2.empty()){//只剩一堆小的，需要用最后一根补
            while(!q1.empty()){
                int u=q1.front();
                q1.pop();
                ans[++num]=node(u,d[u],pos,K-d[u]);
            } 
            break;
        }
        int u=q1.front();
        q1.pop();
        while(d[u]<K){
            if(q2.empty()) break;
            int v=q2.front();
            q2.pop();
            ans[++num]=node(u,d[u],v,K-d[u]);
            d[v]-=K-d[u];
            u=v;
        }
        if(d[u]==K){
            ans[++num]=node(u,K,0,0);
        }else if(d[u]>K)q2.push(u);
        else q1.push(u);
    }
    clear();
}

void solve2(){
    work(N,M);
    print();
}

void solve3(){
    for(int i=1;i<=N;i++){
        tmp[i]=d[i];
        d[i]-=K;
        dp[0]=0;
        vis[i]=0;
    }
    int mx=N*K;
    dp[0]=0;
    dp[0][mx]=1;
    for(int i=1;i<=N;i++){
        if(d[i]>0) dp[i]=dp[i-1]|(dp[i-1]<<d[i]);
        else dp[i]=dp[i-1]|(dp[i-1]>>(-d[i]));
    }
    if(!dp[N][mx-K]){
        puts("-1");
        return;
    }
    int pre=mx-K;
    int m=0;
    for(int i=N;i>=1;i--){
        if(dp[i-1][pre-d[i]]){
            vis[i]=1;
            m++;
            pre-=d[i];
        }
    }
    for(int i=1;i<=N;i++){
        if(vis[i]) d[i]=tmp[i];
        else d[i]=0;
    }
    work(N,m-1);
    for(int i=1;i<=N;i++){
        if(vis[i]) d[i]=0;
        else d[i]=tmp[i];
    }
    m=N-m;
    work(N,m-1);
    print();
}

void init(){
    num=0;
    for(int i=1;i<=M;i++) ans[i].d1=ans[i].d2=ans[i].id1=ans[i].id2=0;
}

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d%d%d",&N,&M,&K);
        init();
        for(int i=1;i<=N;i++) scanf("%d",&d[i]);
        if(M>=N) solve1();
        else if(M==N-1) solve2();
        else solve3();
    }
    return 0;
}
View Code

 

 

 

D2T2.超现实树

 

我们先定义，一棵树是特别的，仅当这棵树每个节点的左右儿子的size中的较小值都小于等于1

直观点就是一个上面长了零星几个叶子的链

我们可以得到这么几个结论

  1. 每一颗树一定能由一棵深度小于等于它的特别的树长成。（这里不要理解错了，不是一棵特别的树可以长成任意深度大于等于它的树，而是你可以从所有深度小于等于这棵树的特别的树中找到至少一颗能满足条件的）这个都不用证吧，纸上画画就明白了。

  2. 一个森林是完备的，仅当有限个特别的树不在森林里。因为只要一定深度的特别的树可以生成，则这个深度以上的所有树都可以被生成。

  3. 不是特别的树对我们没有用处。（我们只关心特别的树能不能生成，不是特别的树生成不了特别的树

然后我们考虑递归判断森林是否完备

我们把筛选出来的特别的树分为4类

  1. 只有左儿子，继续递归左儿子

  2. 只有右儿子，继续递归右儿子

  3. 左右儿子都有，但右儿子size为1，递归左儿子

  4. 左右儿子都有，但左儿子size为1，递归右儿子

最后两种情况会有重叠，但是不影响答案

对于一个森林，有两种情况该森林是完备的：有单点，直接返回完备/四种情况都完备（因为如果有一种情况未完备，就有无限个无法生成的树）

具体见代码

#include<bits/stdc++.h>

using namespace std;

const int MAXN=2e6+5;

typedef pair<int,int> pii;

int T,M;

struct node{
    int *sz,*ls,*rs,N;
    void in(){
        scanf("%d",&N);
        ls=new int[N+5];
        rs=new int[N+5];
        sz=new int[N+5];
        sz[0]=0;
        for(int i=1;i<=N;i++){
            scanf("%d%d",&ls[i],&rs[i]);
        }
    }
    bool check(int x){
        if(ls[x]&&!check(ls[x])) return false;
        if(rs[x]&&!check(rs[x])) return false;
        sz[x]=sz[ls[x]]+sz[rs[x]]+1;
        if(!ls[x]||!rs[x]) return true;
        if(min(sz[ls[x]],sz[rs[x]])>1) return false;
        else return true;
    }
    void clear(){
        for(int i=0;i<=N;i++) sz[i]=ls[i]=rs[i]=0;
    } 
}tr[MAXN];

bool solve(vector<pii> &q){
    if(q.empty()) return false;
    for(int i=0;i<(int)q.size();i++){
        int id=q[i].first;
        int u=q[i].second;
        if(tr[id].sz[u]==1) return true; 
    } 
    vector<pii>q1,q2;//只有右儿子，只有左儿子 
    vector<pii>q3,q4;//左右儿子都有，一个右儿子为1 ，一个左儿子为1
    for(int i=0;i<(int)q.size();i++){
        int id=q[i].first;
        int u=q[i].second;
        if(!tr[id].ls[u]) q1.push_back(make_pair(id,tr[id].rs[u]));
        if(!tr[id].rs[u]) q2.push_back(make_pair(id,tr[id].ls[u]));
        if(tr[id].sz[tr[id].ls[u]]==1&&tr[id].rs[u]) q4.push_back(make_pair(id,tr[id].rs[u]));
        if(tr[id].sz[tr[id].rs[u]]==1&&tr[id].ls[u]) q3.push_back(make_pair(id,tr[id].ls[u]));
    } 
    q.clear();
    if(!solve(q1)||!solve(q2)||!solve(q3)||!solve(q4)) return false;
    return true;
}

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&M);
        int num=0;
        vector<pii> q;
        for(int i=1;i<=M;i++){
            ++num;
            tr[num].in();
            if(!tr[num].check(1)){
                tr[num].clear();
                num--;    
            }else q.push_back(make_pair(num,1));
        }
        if(solve(q)) puts("Almost Complete");
        else puts("No");
        for(int i=1;i<=num;i++) tr[i].clear();
    }
    return 0;
}
View Code

 

posted @ 2020-08-23 14:26  EDawn  阅读(55)  评论(0)    收藏  举报