LeetCode 1557. Minimum Number of Vertices to Reach All Nodes

原题链接在这里：https://leetcode.com/problems/minimum-number-of-vertices-to-reach-all-nodes/description/

题目：

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

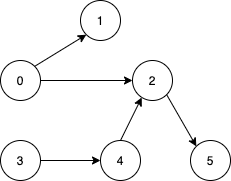
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

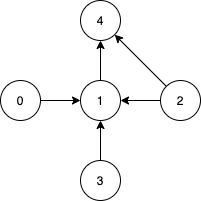
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• All pairs (fromi, toi) are distinct.

题解：

All the nodes with no indegree should be in the final result.

Because node with indegree, they can be reached by some other nodes. And nodes with no indegree can't be reached by any other nodes.

Time Complexity: O(n + e). e = edges.size().

Space: O(n).

AC Java:

class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        List<Integer> res = new ArrayList<>();
        int [] inDegree = new int[n];
        for(List<Integer> e : edges){
            inDegree[e.get(1)]++;
        }

        for(int i = 0; i < n; i++){
            if(inDegree[i] == 0){
                res.add(i);
            }
        }

        return res;
    }
}