LeetCode 1411. Number of Ways to Paint N × 3 Grid

原题链接在这里：https://leetcode.com/problems/number-of-ways-to-paint-n-3-grid/description/

题目：

You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).

Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 109 + 7.

Example 1:

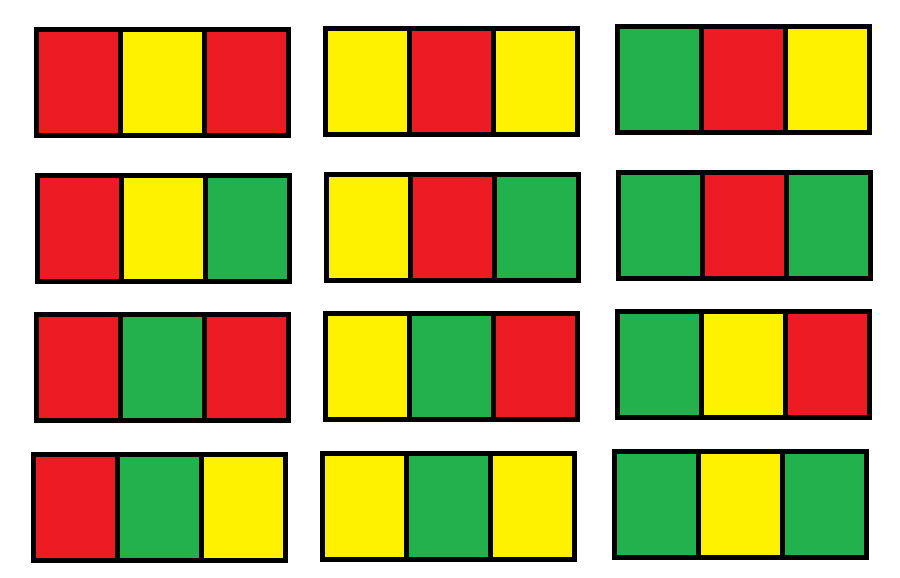
Input: n = 1
Output: 12
Explanation: There are 12 possible way to paint the grid as shown.

Example 2:

Input: n = 5000
Output: 30228214

Constraints:

  • n == grid.length
  • 1 <= n <= 5000

题解：

First calculate the possibilities of first row. Then keep adding the next row. The new row relies on previous row selections.

For the first row, there are 2 choices, one is 3 different colors or 2 different colors.

3 different colors have 6 arrangements. 123, 132, 213, 231, 312, 321

2 different colors have 6 arrangements. 121, 131, 212, 232, 313, 323

For the next row, 3 colors => two 3 colors + two 2 colors

2 colors => three 3 colors + two 2 colors.

Thus, 

long newC3 = (2 * c3 + 2 * c2) % M;
long newC2 = (2 * c3 + 3 * c2) % M;

Time Complexity: O(n).

Space: O(1).

AC Java:

 1 class Solution {
 2     static int M = (int)(1e9 + 7);
 3     public int numOfWays(int n) {
 4         long c3 = 6;
 5         long c2 = 6;
 6         for(int i = 2; i <= n; i++){
 7             long newC3 = (2 * c3 + 2 * c2) % M;
 8             long newC2 = (2 * c3 + 3 * c2) % M;
 9             c3 = newC3;
10             c2 = newC2;
11         }
12 
13         return (int)((c2 + c3) % M);
14     }
15 }

类似Paint Fence.

posted @ 2024-06-02 23:44  Dylan_Java_NYC  阅读(6)  评论(0)  编辑  收藏  举报