网络流小全
简介
这篇文章介绍了关于网络流的一些基本知识点,限于个人水平,本文可能存在谬误,希望发现的读者指正。
问题引入
因为一些不可描述的原因,一些水管从$Kirino$家通向了$Ayase$家,现已知每条水管能承受的水流量,问如果$Kirino$源源不断地从源头注水,$Ayase$这边会得到的最大流量是多少。
概念
首先介绍一下必要的概念。
源点:仅有流量流出的点。
汇点:仅有流量流入的点。
容量:一条有向边最多可以承载的流量大小。
流量:一条有向边已经承载的流量大小。
增广路:一条从源点到汇点上各条边的剩余流量都大于$0$的路径。
残量网络:任意时刻,网络中所有节点以及剩余容量大于$0$的边构成的子图。
性质
容量限制:一条边的流量不大于容量。
流量守恒:除了源点和汇点,任何点不存储流,其流入总量等于流出总量。
反对称性:每条反向边的流量是正向边的流量的相反数。
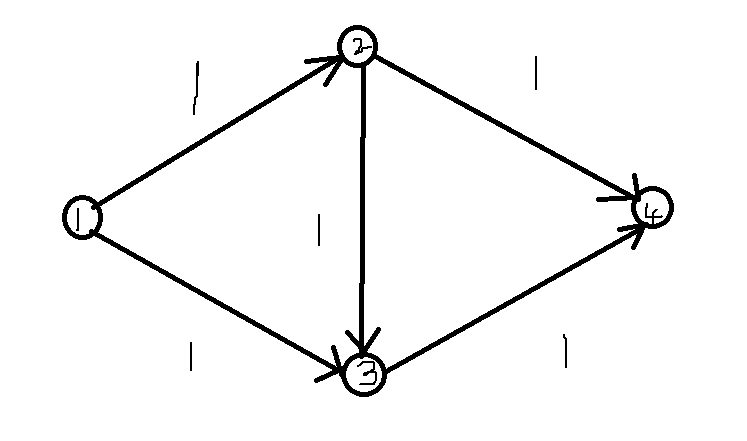
对于这张图显然有$1-2-3-4$和$1-2-4,1-3-4$这两种流法,但是后者明显优于前者,建反边就是为了在最大流算法中解决这个问题。当我们走了$1-2-3-4$这条路之后,由于反向边的存在,我们会在下一次计算中走出$1-3-2-4$将这两条路线重叠在一起得到的结果即针对这张图的最优解。接下来我们讨论如何用成体系的方法求解最大流。
$EK$增广路算法
$EK$的基本思想就是用$bfs$不断地在网络上寻找增广路,得到该增广路上的最小剩余容量$minf$,答案加上$minf$。
每次寻找的时候只考虑容量大于当前流量的边,当一条边$i$被考虑时根据反对称性显然有其反边$i\oplus1$满足这个条件,所以寻找过程中会考虑反向边。由于建图过程中边的编号是从$0$开始的,所以第$i$条正向边对应的反向边显然为$i\oplus1$。更新增广路信息的同时需要记录前驱结点的点编号与边编号方便统计当前增广路对答案的贡献。时间复杂度$O(nm^{2})$。
参考代码:
#include <bits/stdc++.h>
#define DBG(x) cerr << #x << " = " << x << endl
using namespace std;
typedef long long LL;
const int N = 1e5 + 5;
const int M = 2e5 + 5;
const int inf = 0x3f3f3f3f;
int head[N], tot;
bool vis[N];
struct Enode {
int to, next, flow;
} edge[M];
struct Pnode {
int pid, eid;
} pre[N];
void addedge(int u, int v, int f) {
edge[tot].to = v;
edge[tot].flow = f;
edge[tot].next = head[u];
head[u] = tot++;
}
bool bfs(int s, int t) {
memset(vis, false, sizeof vis);
queue<int> q;
q.push(s), vis[s] = 1;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = head[x]; i != -1; i = edge[i].next) {
int v = edge[i].to;
if (!vis[v] && edge[i].flow) {
pre[v].pid = x;
pre[v].eid = i;
vis[v] = 1;
if (v == t) return true;
q.push(v);
}
}
}
return false;
}
LL EK(int s, int t) {
LL res = 0;
while (bfs(s, t)) {
LL minv = inf;
for (int i = t; i != s; i = pre[i].pid) minv = min(minv, 1LL * edge[pre[i].eid].flow);
for (int i = t; i != s; i = pre[i].pid) {
edge[pre[i].eid].flow -= (int)minv;
edge[pre[i].eid ^ 1].flow += (int)minv;
}
res += minv;
}
return res;
}
int main() {
memset(head, -1, sizeof head);
int n, m, s, t;
scanf("%d%d%d%d", &n, &m, &s, &t);
for (int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
addedge(u, v, w);
addedge(v, u, 0);
}
printf("%lld\n", EK(s, t));
return 0;
}
$Dinic$算法
$EK$算法每次只能找出一条增广路,效率还有待提高。我们看看$Dinic$的过程。
$Dinic$不断重复以下步骤,直到不存在$S$到$T$的增广路:
$1$.在残量网络上$bfs$构造分层图。
$2$.在分层图上$dfs$寻找增广路,更新路径信息,答案加上得到的流量。
$Dinic$有两个优化:
$1$.当前弧优化,即每次考虑某个点的出边时只考虑那些还没被增广的,因为如果一条边已经被增广过,那么它就没有可能被增广第二次。
$2$.多路增广,每次找到一条增广路的时候,如果残余流量没有用完怎么办呢?我们可以利用残余部分流量,再找出一条增广路。这样就可以在一次 $dfs$ 中找出多条增广路。
时间复杂度$O(n^{2}m)$在求解二分图最大匹配时可以达到$O(m\sqrt{n})$。
$ps:$由于我自己在写题过程中没有因为没加多路增广优化而被卡掉过,所以给出的代码是单路增广的版本,有需要的同学可以自行探索或生产。
参考代码:
struct Dinic {
static const int maxn = 1e6+5;
static const int maxm = 4e6+5;
struct Edge {
int u, v, next, flow, cap;
} edge[maxm];
int head[maxn], level[maxn], cur[maxn], eg;
void addedge(int u, int v, int cap) {
edge[eg]={u,v,head[u],0,cap},head[u]=eg++;
edge[eg]={v,u,head[v],0, 0},head[v]=eg++;
}
void init() {
eg = 0;
memset(head, -1, sizeof head);
}
bool makeLevel(int s, int t, int n) {
for(int i = 0; i < n; i++) level[i] = 0, cur[i] = head[i];
queue<int> q; q.push(s);
level[s] = 1;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = edge[i].next) {
Edge &e = edge[i];
if(e.flow < e.cap && level[e.v] == 0) {
level[e.v] = level[u] + 1;
if(e.v == t) return 1;
q.push(e.v);
}
}
}
return 0;
}
int findpath(int s, int t, int limit = INT_MAX) {
if(s == t || limit == 0) return limit;
for(int i = cur[s]; ~i; i = edge[i].next) {
cur[edge[i].u] = i;
Edge &e = edge[i], &rev = edge[i^1];
if(e.flow < e.cap && level[e.v] == level[s] + 1) {
int flow = findpath(e.v, t, min(limit, e.cap - e.flow));
if(flow > 0) {
e.flow += flow;
rev.flow -= flow;
return flow;
}
}
}
return 0;
}
int max_flow(int s, int t, int n) {
int ans = 0;
while(makeLevel(s, t, n)) {
int flow;
while((flow = findpath(s, t)) > 0) ans += flow;
}
return ans;
}
} di;
最小割定理
给定一个网络$G=(V,E)$,源点为$S$,汇点为$T$。若一个边集$E^{'}\subseteq E$被删去后,$S$和$T$不再联通,则称该边集为网络的割。边容量之和的最小的割称为网络的最小割。
一个网络的最小割等于它的最大流。
费用流
问题引入
由于$Kirino$家的水全排到了$Ayase$家,她为了补偿$Ayase$决定给每条水管都附一个价值$c$,当$f$数量的流量流过时$Kirino$会补偿给$Ayase$的钱为$c*f$。问在流量最大的前提下$Kirino$最少要补偿多少钱。
基于$EK$的费用流算法
在最大流的$EK$算法求解最大流的基础上,把用$bfs$求解任意增广路改为用$spfa$求解费用之和最小的增广路即可,相当于把花费$w(x,y)$作为边权,在残存网络上求最短路。需要注意的是,一条反向边$(y, x)$的费用应该设置为$-w(x, y)$。
容易想到,如果问题要求我们考虑的时最大费用,我们只需在$spfa$的过程中维护最大费用,做法是建边时使用负边权,做完最短路处理之后得到的答案取反。
struct MCMF {
static const int maxn = 200 + 5;
static const int maxm = 1e5 + 5;
int eg, pre[maxn], dis[maxn], head[maxn], vis[maxn];
struct node {
int u, v, c, f, next;
} edge[maxm];
void add(int u, int v, int c, int f) {
edge[eg] = {u, v, c, f, head[u]}, head[u] = eg++;
edge[eg] = {v, u, -c, 0, head[v]}, head[v] = eg++;
}
queue<int> q;
bool spfa(int S,int T, int sz) {
for(int i = 0; i <= sz; i++) pre[i] = -1, vis[i] = 0;
for(int i = S; i <= T; i++) dis[i] = inf;
while(!q.empty()) q.pop();
q.push(S);
dis[S] = 0;
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = head[u]; i != -1; i = edge[i].next) {
int v = edge[i].v;
if(edge[i].f && dis[v] > dis[u] + edge[i].c) {
dis[v] = dis[u] + edge[i].c;
pre[v] = i;
if(!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
vis[u] = 0;
}
return dis[T] != inf;
}
int solve(int S,int T, int sz) {
int flow = 0, cost = 0;
while(spfa(S, T, sz)) {
int mn = inf;
for(int i = pre[T]; i != -1; i = pre[edge[i].u]) {
if(edge[i].f < mn) mn = edge[i].f;
}
flow += mn;
for(int i = pre[T]; i != -1; i = pre[edge[i].u]) {
edge[i].f -= mn;
edge[i ^ 1].f += mn;
}
cost += dis[T] * mn;
}
return cost;
}
void init() {
eg = 0;
memset(head, -1, sizeof head);
}
} mc;
上下界网络流
无源汇上下界可行流
一张网络中没有源点和汇点,每条边的流量都被限制在区间$[L_i,R_i]$中,问该网络中达到可行流量下每条边的流量。
首先每条边必然要满足下界,我们称此时的流量为初始流,显然此时的网络不一定满足流量守恒,为了满足流量守恒,我们建立超级源点$SS$和超级汇点$TT$,为每个可能不满足流量守恒的点提供附加流,显然对于一条流量下限为$L_i$的有向边$(u, v)$,需要为$u$点的附加流减去$L_i$贡献,为$v$加上$L_i$贡献。之后求解最大流,如果最大流满流,即$maxflow=sum$其中$sum$为所有超源所连向的点的附加流,那么这个当前方案是可行的。
有源汇上下界可行流
一张网络中有源点和汇点$S,T$,每条边的流量都被限制在区间$[L_i,R_i]$中,问该网络中达到可行流量下每条边的流量以及$S$到$T$的流量。
将$T$到$S$连一条流量为$inf$的边,此时就转化成了无源汇的情况。
由于流量守恒对于$S$和$T$依然成立且流入$S$的边仅有$(T,S)$一条,所以根据流量守恒可知边$(T,S)$上的流量即原图上的可行流,根据反向边的性质,这个信息正好被记录在了$(T,S)$的反向边上的流量。
有源汇上下界最大流
当条件变成求最大流之后,我们首先考虑求出可行流,如果可行,我们只需要再在残量网络上以初始的源点和汇点$S,T$求一次最大流,答案显然就是可行流的流量加上残量网络上最大流的流量。
有源汇上下界最小流
先给做法:
$1$.根据附加流建立加入超源超汇$SS,TT$的图,对$(SS,TT)$做一次最大流。
$2$.原图连一条$(T,S)$流量为$inf$的边,对$(SS,TT)$做一次最大流。
$3$.当附加边都满流时,答案为$(T,S)$反向边上的流量。
粗略证明:不加$(T,S)$时求过一次最大流,此时尽可能使能流的流量流入了不会增大答案的边,此时再连上$(T,S)$后跑最大流,如果附加流满流,那么就可以达到减小最终答案的目的。
最大权闭合子图
闭合图是什么?在一个图中,我们选取一些点构成集合,若集合中任意点连接的任意出弧,所指向的终点也在该点集中,则这个集合以及所有这些边构成闭合图。最大权闭合子图即点权之和最大的闭合图。求一张图的最大权闭合子图的步骤如下:
$1$.建立源点$S$连向正权点,流量为点的权值。建立汇点$T$,令所有负权点连向$T$,流量为点权值的绝对值。点与点之间根据原来的方向顺序连流量为$inf$的边。
$2$.图$G$的最大权闭合子图$G^{'}$的权值和为所有$G$中的正点权和$sum$减去$S$到$T$的最大流$flow$。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号