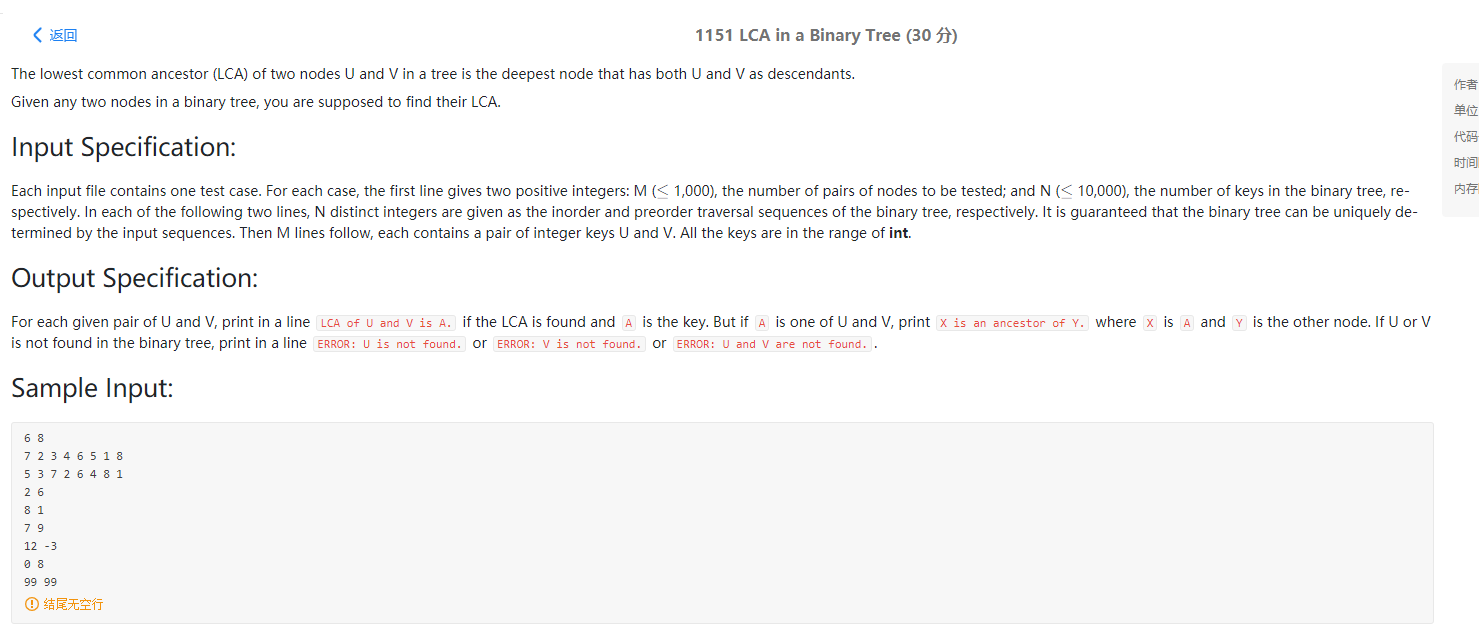
1151 LCA in a Binary Tree (30 分)

两种解法
【解法一】
树上倍增求LCA

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn = 1000005;
typedef struct node {
    ll val;
    node *l, *r;
} node;
ll pre[maxn];
ll in[maxn];
ll n, m;
ll l[maxn];
ll r[maxn];
map<ll,ll>mp;
ll lg[maxn];
ll dep[maxn];
ll fa[maxn][30];
ll z[maxn];
node* build(ll& l, ll r, ll l1, ll r1) {//前序与中序建树
    node* p = new node;
    p->val = pre[l];
    ll k = -1;
    for (ll i = l1; i <= r1; i++) {
        if (pre[l] == in[i]) {
            k = i;
            break;
        }
    }
    if (k == -1)
        return nullptr;
    if (k - 1 >= l1) {
        l++;
        p->l = build(l, r, l1, k - 1);
    } else
        p->l = nullptr;
    if (k + 1 <= r1) {
        l++;
        p->r = build(l, r, k + 1, r1);
    } else
        p->r = nullptr;
    return p;
}
void dfs(node *p)//书上倍增求父亲
{
    ll x=p->val;
    for(ll i=1;i<=lg[dep[x]];i++)
    {
        if(fa[x][i-1])
        {
            fa[x][i]=fa[fa[x][i-1]][i-1];
        }
        else break;
    }
    if(p->l)
    {
        ll v=p->l->val;
         fa[v][0]=x;
         dep[v]=dep[x]+1;
         dfs(p->l);

    }
    if(p->r)
    {
         ll v=p->r->val;
          fa[v][0]=x;
         dep[v]=dep[x]+1;
         dfs(p->r);
    }
}
ll lca(ll x,ll y)
{
    ll flag=0;
    if(dep[x]<dep[y]) swap(x,y);
    for(ll i=lg[dep[x]];i>=0;i--)
    {
        if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
        if(x==y) return x;
    }
    for(ll i=lg[dep[x]];i>=0;i--)
    {
        if(fa[x][i]!=fa[y][i])
        {
            x=fa[x][i];
            y=fa[y][i];
        }
        else 
        {
            flag=1;
        }
    }
    if(!flag) return -1;
    else 
    return fa[x][0];
}
int main() {
    cin >> m >> n;
     for (int i = 1; i <= n; i++)
        lg[i] = lg[i - 1] + (1<<lg[i - 1] == i);
    for (ll i = 1; i <= n; i++) {
        cin >> in[i];
        mp[in[i]]=1;
    }
    for (ll i = 1; i <= n; i++) {
        cin >> pre[i];
    }
    ll s = 1;
    node* root = build(s, n, 1, n);
    dep[root->val]=1;
    dfs(root);
    for (ll i = 1; i <= m; i++) {
        cin >> l[i] >> r[i];
        z[i]=lca(l[i],r[i]);
    }
    for(ll i=1;i<=m;i++)
    {
       
           if(!mp[l[i]]&&!mp[r[i]])
           {
               cout<<"ERROR: "<<l[i]<<" and "<<r[i]<<" are not found."<<endl;
           }
           else if(!mp[l[i]])
           {
               cout<<"ERROR: "<<l[i]<<" is not found."<<endl;
           }
           else if(!mp[r[i]])
           {
               cout<<"ERROR: "<<r[i]<<" is not found."<<endl;
           }
            else{ 
           if(z[i]==l[i])
           {
               cout<<l[i]<<" is an ancestor of "<<r[i]<<"."<<endl;
           }
           else if(z[i]==r[i])
           {
               cout<<r[i]<<" is an ancestor of "<<l[i]<<"."<<endl;
           }
           else 
           {
               cout<<"LCA of "<<l[i]<<" and "<<r[i]<<" is "<<z[i]<<"."<<endl;
           }
            }
    }
    return 0;
}

【解法二】
tarjan并查集求LCA

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn = 1000005;
typedef struct node {
    ll val;
    node *l, *r;
} node;
ll pre[maxn];
ll in[maxn];
ll n, m;
ll l[maxn];
ll r[maxn];
ll s[maxn];
ll vis[maxn];
ll z[maxn];
map<ll,ll>mp;
ll find(ll x) {
    if (x != s[x]) {
        return s[x] = find(s[x]);
    } else
        return s[x];
}
void init()
{
    for(ll i=0;i<=1000005;i++){
        vis[i]=0;
        s[i]=i;
        z[i]=-1;
    }
}
void lca(node* p,node* pre) {
    if (p->l) {             //dfs
        lca(p->l,p);
        ll x=find(p->val);
        ll y=find(p->l->val);
        if(x!=y)
        {
            s[y]=x;
        }
    }
    if (p->r) {
        lca(p->r,p);
        ll x=find(p->val);
        ll y=find(p->r->val);
        if(x!=y)
        {
            s[y]=x;
        }
    }
    vis[p->val]=1;          //标记该点以及该点的子树已经被遍历完成
    for(ll i=1;i<=m;i++)
    {
        if(vis[l[i]]&&vis[r[i]])    //如果两个点都被标记完成
        {
            if(l[i]==p->val)            //且其中有一个点是当前点
            {
                z[i]=find(r[i]);
            }
            else if(r[i]==(p->val)) 
            {
                z[i]=find(l[i]);
            }
            else continue;
        }
    }
}
node* build(ll& l, ll r, ll l1, ll r1) {//前序与中序建树
    node* p = new node;
    p->val = pre[l];
    ll k = -1;
    for (ll i = l1; i <= r1; i++) {
        if (pre[l] == in[i]) {
            k = i;
            break;
        }
    }
    if (k == -1)
        return nullptr;
    if (k - 1 >= l1) {
        l++;
        p->l = build(l, r, l1, k - 1);
    } else
        p->l = nullptr;
    if (k + 1 <= r1) {
        l++;
        p->r = build(l, r, k + 1, r1);
    } else
        p->r = nullptr;
    return p;
}
int main() {
    cin >> m >> n;
    for (ll i = 1; i <= n; i++) {
        cin >> in[i];
        mp[in[i]]=1;
    }
    for (ll i = 1; i <= n; i++) {
        cin >> pre[i];
    }
    ll s = 1;
    node* root = build(s, n, 1, n);
    for (ll i = 1; i <= m; i++) {
        cin >> l[i] >> r[i];
    }
    node *pre=new node;
    init();
    pre->val=1000005;
    lca(root,pre);
    for(ll i=1;i<=m;i++)
    {
       if(z[i]==-1)
       {
           if(!mp[l[i]]&&!mp[r[i]])
           {
               cout<<"ERROR: "<<l[i]<<" and "<<r[i]<<" are not found."<<endl;
           }
           else if(!mp[l[i]])
           {
               cout<<"ERROR: "<<l[i]<<" is not found."<<endl;
           }
           else 
           {
               cout<<"ERROR: "<<r[i]<<" is not found."<<endl;
           }
       }
       else
       {
           if(z[i]==l[i])
           {
               cout<<l[i]<<" is an ancestor of "<<r[i]<<"."<<endl;
           }
           else if(z[i]==r[i])
           {
               cout<<r[i]<<" is an ancestor of "<<l[i]<<"."<<endl;
           }
           else 
           {
               cout<<"LCA of "<<l[i]<<" and "<<r[i]<<" is "<<z[i]<<"."<<endl;
           }
       }
    }
    return 0;
}