The 10th Shandong Provincial Collegiate Programming Contest
Contest Info
[Practice Link](https://cn.vjudge.net/contest/303285)
| Solved | A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12/13 | O | O | O | O | O | O | - | O | Ø | Ø | O | O | O |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
A. Calandar
签到题。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
int y[2], m[2], d[2];
map <string, int> mp;
string ss[10], s;
int main() {
mp["Monday"] = 1;
mp["Tuesday"] = 2;
mp["Wednesday"] = 3;
mp["Thursday"] = 4;
mp["Friday"] = 5;
ss[1] = "Monday";
ss[2] = "Tuesday";
ss[3] = "Wednesday";
ss[4] = "Thursday";
ss[5] = "Friday";
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int T; cin >> T;
while (T--) {
cin >> y[0] >> m[0] >> d[0] >> s;
cin >> y[1] >> m[1] >> d[1];
int now = mp[s] - 1;
int add = 0;
if (d[1] >= d[0]) {
add += d[1] - d[0];
} else {
add += 30 - d[0] + d[1];
}
now = (now + add) % 5;
cout << ss[now + 1] << "\n";
}
return 0;
}
B. Flipping Game
题意:
有两个01串\(s, t\),每一轮在\(s\)串中选择任意\(m\)个进行翻转\(0 \rightarrow 1, 1 \rightarrow 0\),求恰好\(k\)轮之后\(s\)变成\(t\)的方案数。
思路:
\(f[i][j]\)表示在第\(i\)轮,有\(j\)个在正确位置上的方案数,组合数转移即可。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 110
int n, k, m;
const ll p = 998244353;
ll f[N][N];
char st[N], ed[N];
ll inv[N], fac[N];
ll qmod(ll base, ll n) {
ll res = 1;
while (n) {
if (n & 1) {
res = res * base % p;
}
base = base * base % p;
n >>= 1;
}
return res;
}
ll C(int n, int m) {
if (n == 0 && m == 0) {
return 1;
}
if (n < m) {
return 0;
}
return 1ll * fac[n] * inv[m] % p * inv[n - m] % p;
}
void init() {
for (int i = 0; i <= k; ++i) {
for (int j = 0; j <= n; ++j) {
f[i][j] = 0;
}
}
}
int main() {
fac[0] = 1;
for (int i = 1; i < N; ++i) {
fac[i] = fac[i - 1] * i % p;
}
inv[100] = qmod(fac[100], p - 2);
for (int i = 100; i >= 1; --i) {
inv[i - 1] = inv[i] * i % p;
}
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d%d", &n, &k, &m);
init();
scanf("%s%s", st + 1, ed + 1);
int ini = 0;
for (int i = 1; i <= n; ++i) {
ini += (st[i] == ed[i]);
}
//f[i][j] 表示第i轮 有j个在正确位置上
f[0][ini] = 1;
for (int i = 1; i <= k; ++i) {
for (int j = 0; j <= n; ++j) {
//当j >= o 的时候
for (int o = 0; o <= j; ++o) {
int gap = j - o;
if (m >= gap && (m - gap) % 2 == 0) {
//表示把x个正确的翻转成不正确的
int x = (m - gap) / 2;
//表示把y个不正确的翻转成正确的
int y = x + gap;
(f[i][j] += C(o, x) * C(n - o, y) % p * f[i - 1][o] % p) %= p;
}
}
//当j < o 的时候
for (int o = j + 1; o <= n; ++o) {
int gap = o - j;
if (m >= gap && (m - gap) % 2 == 0) {
//表示把x个不正确的翻转成正确的
int x = (m - gap) / 2;
//表示把y个正确的翻转成不正确的
int y = x + gap;
(f[i][j] += C(o, y) * C(n - o, x) % p * f[i - 1][o] % p) %= p;
}
}
}
}
// puts("#####################################");
// for (int i = 1; i <= k; ++i) {
// for (int j = 0; j <= n; ++j) {
// printf("%d %d %lld\n", i, j, f[i][j]);
// }
// }
printf("%lld\n", f[k][n]);
}
return 0;
}
C. Wandering Robot
题意:
机器人从\((0, 0)\)出发,现在要求走\(k\)轮,每轮走\(n\)步,求这个过程中的最大曼哈顿距离。
思路:
暴力第\(1\)轮以及第\(k\)轮,中间的轮数直接加上一轮的结果就好了。
因为如果一轮的行走结果导致曼哈顿距离变小的话,那么不可能通过走若干个完整轮 + 一个部分轮达到最有解。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 100010
int n, k;
char s[N];
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &k);
scanf("%s", s + 1);
ll x = 0, y = 0;
ll res = 0;
for (int i = 1; i <= n; ++i) {
if (s[i] == 'L') {
--x;
} else if (s[i] == 'R') {
++x;
} else if (s[i] == 'U') {
--y;
} else if (s[i] == 'D') {
++y;
}
res = max(res, abs(x) + abs(y));
}
ll tmp = 1ll * (k - 1) * (abs(x) + abs(y));
res = max(res, tmp);
ll nx = 1ll * (k - 1) * x, ny = 1ll * (k - 1) * y;
for (int i = 1; i <= n; ++i) {
if (s[i] == 'L') {
--nx;
} else if (s[i] == 'R') {
++nx;
} else if (s[i] == 'U') {
--ny;
} else if (s[i] == 'D') {
++ny;
}
res = max(res, abs(nx) + abs(ny));
}
printf("%lld\n", res);
}
return 0;
}
D. Game on a Graph
题意:
两个队伍的人在一张图上进行博弈,每次每个人轮流选择一条边删去,谁删去之后图不连通了,那么这个人所属的队伍就输了。
思路:
显然,可移动的边只有\(m - (n - 1)\)条。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define N 100010
int k, n, m;
int a[N];
char s[N];
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d", &k);
scanf("%s", s + 1);
for (int i = 1; i <= k; ++i) {
a[i] = s[i] - '0';
}
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) scanf("%*d%*d");
int tot = (m - (n - 1));
printf("%d\n", ((a[tot % k + 1] - 1) ^ 1) + 1);
}
return 0;
}
E. BaoBao Loves Reading
题意:
询问\(Least\;Recently\;Used (LRU)\)算法进行换页操作的时候,页表容量为\(1, \cdots, n\)的时候的换页次数分别为多少
思路:
我们考虑以下不用换页的次数,根据\(LRU\)算法的特性,我们注意到两个相同页之间的不同页个数如果为\(x\),那么当页表容量$ > x$的时候这一次换页是不需要的。
树状数组+前缀和维护一下即可。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define N 101010
int n, a[N], b[N], pre[N];
struct BIT {
int a[N];
void init(int n) {
for (int i = 0; i <= n + 10; ++i) {
a[i] = 0;
}
}
void update(int x, int val) {
for (; x < n + 10; x += x & -x) {
a[x] += val;
}
}
int query(int x) {
int res = 0;
for (; x > 0; x -= x & -x) {
res += a[x];
}
return res;
}
}bit;
void init() {
for (int i = 0; i <= n; ++i) {
b[i] = 0;
pre[i] = 0;
}
bit.init(n);
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d", &n);
init();
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
}
for (int i = 1; i <= n; ++i) {
if (pre[a[i]]) {
int tot = bit.query(i) - bit.query(pre[a[i]]);
++b[tot + 1];
bit.update(pre[a[i]], -1);
}
bit.update(i, 1);
pre[a[i]] = i;
}
for (int i = 1; i <= n; ++i) {
b[i] += b[i - 1];
printf("%d%c", n - b[i], " \n"[i == n]);
}
}
return 0;
}
F. Stones in the Bucket
题意:
有\(n\)堆石头,两种操作:
- 从一堆非空的石头中移除一个
- 从一堆非空的石头中移动一个到另一堆
询问最少多少次操作使得所有堆的石头个数相同。
思路:
容易发现如果知道最终每堆石头的个数,那么操作次数是固定的,并且具有单调性。
二分即可,注意check是否可以。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 100010
int n, a[N];
ll tot;
bool check(ll x) {
ll remind = 0;
for (int i = 1; i <= n; ++i) {
if (a[i] > x) {
remind += a[i] - x;
}
}
ll tmp = remind;
for (int i = 1; i <= n; ++i) {
if (a[i] < x) {
remind -= x - a[i];
}
}
if (remind >= 0) {
tot = min(tot, tmp);
return true;
}
return false;
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
}
tot = 1e18;
ll l = 0, r = 1e9;
while (r - l >= 0) {
ll mid = (l + r) >> 1;
if (check(mid)) {
l = mid + 1;
} else {
r = mid - 1;
}
}
printf("%lld\n", tot);
}
return 0;
}
H. Tokens on the Segments
题意:
二维平面上有\(n\)条线段,每条线段为\((l_i, i) \rightarrow (r_i, i)\),平面上的每个整点上都可以放置一个令牌,但是要求任意两个令牌的横坐标不相同,问最多有多少条线段上放着令牌。
思路:
先将所有线段按左端点排序,然后从\(Min \rightarrow Max\)枚举线段上每一个点,将左端点小于当前点的所有右端点放进小顶堆,每次取右端点最小的拿出来放在当前点。
注意遍历的时候如果堆空的时候要注意跳跃指针。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
struct node {
int l, r;
node(){}
node(int l, int r):l(l), r(r){}
bool operator < (const node &other) const {
if (l == other.l) return r < other.r;
else return l < other.l;
}
}arr[maxn];
int n;
int main() {
int t;
scanf("%d", &t);
while(t--){
scanf("%d", &n);
int Min = 1e9 + 10;
int Max = 0;
for (int i = 1; i <= n; ++i) {
scanf("%d %d", &arr[i].l, &arr[i].r);
Min = min(Min, arr[i].l);
Max = max(Max, arr[i].r);
}
sort(arr + 1, arr + 1 + n);
int ans = 0;
priority_queue<int, vector<int>, greater<int> >q;
int pos = 0;
for (int i = Min; i <= Max; ++i) {
while(pos <= n && arr[pos].l <= i) q.push(arr[pos++].r);
while(!q.empty() && q.top() < i) q.pop();
if(!q.empty()) {
ans++;
q.pop();
}
if(q.empty()) {
if(pos > n) {
break;
}
i = max(i, arr[pos].l - 1);
}
}
printf("%d\n", ans);
}
return 0;
}
I - Connected Intervals
题意:
给出一棵树,问存在多少个子树(树上的连通块),使得这个连通块里面的点的标号是连续的。
思路:
我们考虑\(ma[i]\)表示\((i, i + 1)\)路径上的标号的最大值,\(mi[i]\)表示\((i, i + 1)路径上的标号的最小值\)。
然后我们考虑一段区间\([l, r]\)这个点在树上是一个连通块,那么当且仅当:
那么我们考虑分治,考虑对于:
- 左边每个点求出\(f_{max}[i]\)表示点\(i\)到\(mid\)这段区间形成任意相邻两点路径上的标号的最大值,同理\(f_{min}[i]\)表示最小值。
- 对于右边每个点求出\(g_{max}[i]\)表示点\(i\)到\(mid\)这段区间形成任意相邻两点路径上的标号的最大值,同理\(g_{min}[i]\)表示最小值。
那么每次分治的时候,我们只统计跨过区间中点\(mid\)的区间个数,这样每个合法区间只会被统计一次。
那么我们考虑枚举左边每个点为左端点,这个点能成为左端点当且仅当\(f_min[i] = i\),然后然后所有右边的点,它能成为右端点当且仅当\(g_{max}[j] = j\)。
那么我们将合法的右端点丢进树状数组维护,每次对于一个左端点,只需要查询\(g_{min}[j] \in [i, n]\)的右端点个数即可。
时间复杂度\(O(nlog^2n)\)
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define dbg(x...) do { cout << "\033[32;1m" << #x << " -> "; err(x); } while (0)
void err() { cout << "\033[39;0m" << endl; }
template <class T, class... Ts> void err(const T& arg, const Ts&... args) { cout << arg << ' '; err(args...); }
using ll = long long;
using pII = pair<int, int>;
#define fi first
#define se second
const int N = 3e5 + 10, M = 23, INF = 0x3f3f3f3f;
int n; ll res;
vector <vector<int>> G;
template <class T1, class T2> void chmax(T1 &x, T2 y) { if (x < y) x = y; }
template <class T1, class T2> void chmin(T1 &x, T2 y) { if (x > y) x = y; }
struct E {
int ma, mi;
E(int ma = -INF, int mi = INF) : ma(ma), mi(mi) {}
void up(E other) {
chmax(ma, other.ma);
chmin(mi, other.mi);
}
}f[N], g[N];
//f 表示路径(i, i - 1) g 表示路径(i, i + 1)
struct W {
int op, ma, mi;
W() {}
W(int op, int ma, int mi) : op(op), ma(ma), mi(mi) {}
}w[N];
struct LCA {
int fa[N][M], deg[N]; E e[N][M];
void bfs() {
queue <int> que;
deg[1] = 0; fa[1][0] = 1;
e[1][0] = E(-INF, INF);
que.push(1);
while (!que.empty()) {
int u = que.front(); que.pop();
for (int i = 1; i < M; ++i) {
e[u][i] = E(-INF, INF);
e[u][i].up(e[u][i - 1]);
e[u][i].up(e[fa[u][i - 1]][i - 1]);
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for (auto &v : G[u]) {
if (v == fa[u][0]) continue;
deg[v] = deg[u] + 1;
fa[v][0] = u;
e[v][0] = E(v, v);
que.push(v);
}
}
}
E dis(int u, int v) {
if (u == v) return E(u, u);
if (deg[u] > deg[v]) swap(u, v);
int hu = deg[u], hv = deg[v], tu = u, tv = v;
E res = E(-INF, INF);
for (int det = hv - hu, i = 0; det; det >>= 1, ++i) {
if (det & 1) {
res.up(e[tv][i]);
tv = fa[tv][i];
}
}
if (tu == tv) {
res.up(E(tu, tu));
return res;
}
for (int i = M - 1; i >= 0; --i) {
if (fa[tu][i] == fa[tv][i]) continue;
res.up(e[tu][i]);
res.up(e[tv][i]);
tu = fa[tu][i]; tv = fa[tv][i];
}
res.up(e[tu][0]);
res.up(e[tv][0]);
res.up(E(fa[tu][0], fa[tu][0]));
return res;
}
}lca;
struct BIT {
int a[N], pos[N], POS;
void init() { POS = 0; }
void update(int x) {
for (; x <= n + 1; x += x & -x) {
if (pos[x] < POS) {
pos[x] = POS;
a[x] = 1;
} else {
++a[x];
}
}
}
int query(int x) {
int res = 0;
for (; x > 0; x -= x & -x) {
if (pos[x] == POS)
res += a[x];
}
return res;
}
int query(int l, int r) {
if (l > r) return 0;
return query(r) - query(l - 1);
}
}bit;
void gao(int l, int r) {
if (l == r) {
++res;
return;
}
int mid = (l + r) >> 1;
gao(l, mid); gao(mid + 1, r);
E now = E(mid, mid);
int cw = 0;
for (int i = mid + 1; i <= r; ++i) {
now.up(f[i]);
if (now.ma == i) {
w[++cw] = W(0, now.ma, now.mi);
}
}
now = E(mid, mid);
for (int i = mid; i >= l; --i) {
if (i < mid) now.up(g[i]);
if (now.mi == i) {
w[++cw] = W(1, now.ma, now.mi);
}
}
sort(w + 1, w + 1 + cw, [&](W x, W y){
if (x.mi != y.mi)
return x.mi > y.mi;
return x.op < y.op;
});
++bit.POS;
for (int i = 1; i <= cw; ++i) {
if (w[i].op == 0) {
bit.update(w[i].ma);
} else {
res += bit.query(w[i].ma, n);
}
}
}
int main() {
bit.init();
int _T; scanf("%d", &_T);
while (_T--) {
scanf("%d", &n);
G.clear(); G.resize(n + 1);
for (int i = 1, u, v; i < n; ++i) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
lca.bfs();
for (int i = 1; i <= n; ++i) f[i] = g[i] = E(-INF, INF);
for (int i = 2; i <= n; ++i) f[i] = lca.dis(i - 1, i);
for (int i = n - 1; i >= 1; --i) g[i] = lca.dis(i, i + 1);
// for (int i = 1; i <= n; ++i) dbg(i, f[i].ma, f[i].mi, g[i].ma, g[i].mi);
res = 0;
gao(1, n);
printf("%lld\n", res);
}
return 0;
}
J. Triangle City
题意:
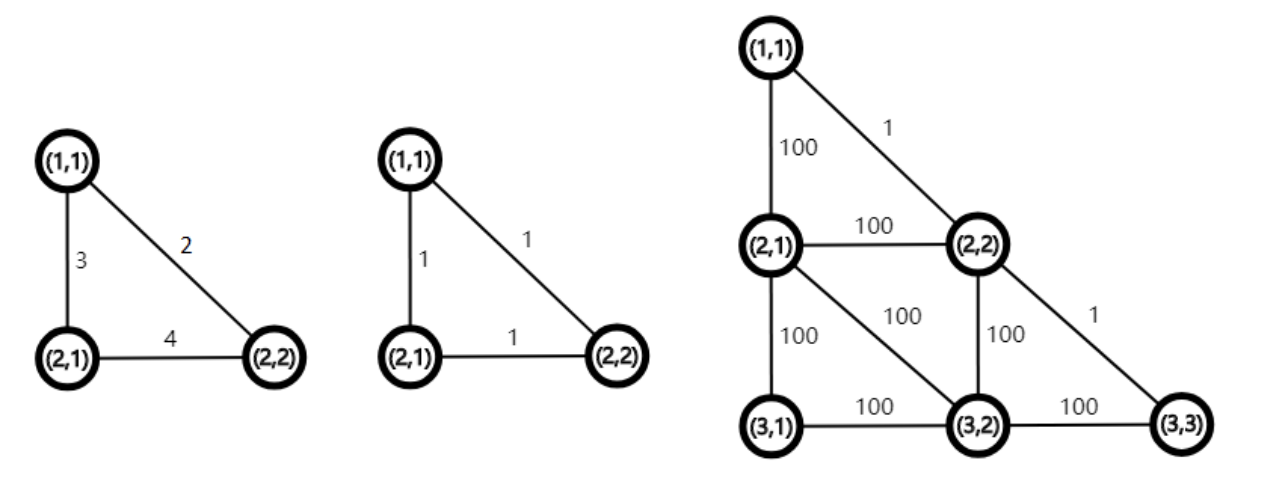
有一个三角形城市,每个点\((i, j)(1 \leq i, j < n)\),都有三条边,\((i, j) \rightarrow (i + 1, j), (i, j) \rightarrow (i + 1, j + 1), (i + 1, j) \rightarrow (i + 1, j + 1)\)。
问\((1, 1) \rightarrow (n, n)\)的最长的路,要求每条边最多出现在最长路上一次。
思路:
边最多出现一次,我们想到欧拉路径,但是欧拉路径要求起点和终点的度数为奇数,其余点的度数为偶数。
可是这张图里面所有点的度数都为偶数,所以我们希望去掉起点的一条边和终点的一条边。
那么可以求一条起点到终点的最短路,这样就使得最短路上的其他点的度数\(- 2\),起点和终点的度数\(- 1\)。再跑一次欧拉路径即可。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define ll long long
#define INFLL 0x3f3f3f3f3f3f3f3f
#define pii pair <int, int>
#define fi first
#define se second
int n;
struct Graph {
struct node {
int to, nx, w, sta;
node () {}
node (int to, int nx, int w) : to(to), nx(nx), w(w) {
sta = 1;
}
}a[N << 2];
int head[N], pos;
void init(int n) {
for (int i = 0; i <= n; ++i) {
head[i] = -1;
}
pos = 0;
}
void add(int u, int v, int w) {
a[pos] = node(v, head[u], w); head[u] = pos++;
a[pos] = node(u, head[v], w); head[v] = pos++;
}
}G;
#define erp(u) for (int it = G.head[u], v = G.a[it].to, w = G.a[it].w; ~it; it = G.a[it].nx, v = G.a[it].to, w = G.a[it].w)
int id(int i, int j) {
return (i - 1) * n + j;
}
pii fid(int x) {
--x;
return pii(x / n + 1, x % n + 1);
}
struct node {
int to, pre; ll w;
node() {}
node (int to, int pre, ll w) : to(to), pre(pre), w(w) {}
bool operator < (const node &other) const {
return w > other.w;
}
};
ll sum;
ll dist[N];
int used[N];
int pre[N];
void Dijkstra() {
for (int i = 1; i <= n * n; ++i) {
dist[i] = INFLL;
used[i] = 0;
pre[i] = i;
}
dist[1] = 0;
priority_queue <node> pq;
pq.push(node(1, -1, 0));
while (!pq.empty()) {
int u = pq.top().to, fa = pq.top().pre; pq.pop();
if (used[u]) {
continue;
}
pre[u] = fa;
used[u] = 1;
if (u == n * n) {
sum -= dist[u];
while (pre[u] != -1) {
erp(u) if (v == pre[u]) {
G.a[it].sta = 0;
G.a[it ^ 1].sta = 0;
break;
}
u = pre[u];
}
}
erp(u) if (!used[v] && dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
pq.push(node(v, u, dist[v]));
}
}
}
vector <int> res;
void DFS(int u) {
erp(u) if (G.a[it].sta == 1) {
G.a[it].sta = 0;
G.a[it ^ 1].sta = 0;
DFS(v);
res.push_back(v);
}
}
void init() {
G.init(n * n + 10);
sum = 0;
res.clear();
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d", &n); init();
for (int i = 1, w; i < n; ++i) {
for (int j = 1; j <= i; ++j) {
scanf("%d", &w);
G.add(id(i, j), id(i + 1, j), w);
sum += w;
}
}
for (int i = 1, w; i < n; ++i) {
for (int j = 1; j <= i; ++j) {
scanf("%d", &w);
G.add(id(i, j), id(i + 1, j + 1), w);
sum += w;
}
}
for (int i = 1, w; i < n; ++i) {
for (int j = 1; j <= i; ++j) {
scanf("%d", &w);
G.add(id(i + 1, j), id(i + 1, j + 1), w);
sum += w;
}
}
Dijkstra();
DFS(1);
res.push_back(1);
reverse(res.begin(), res.end());
printf("%lld\n", sum);
printf("%d\n", (int)res.size());
for (int i = 0, sze = (int)res.size(); i < sze; ++i) {
pii cor = fid(res[i]);
printf("%d %d%c", cor.fi, cor.se, " \n"[i == sze - 1]);
}
}
return 0;
}
K. Happy Equation
题意:
给出\(a, p\)判断有多少个\(x\)满足:
思路:
- \(a, x\)的奇偶性要相同
- \(a\)是奇数的时候,打表发现答案是\(1\)
- \(a\)是偶数的时候:
- 当\(x < p\)时,直接暴力。
- 当\(x \geq p\):
- \(a^p \equiv 0 \bmod p\)
- 考虑如何让\(x^a \equiv 0 \bmod p\), 将\(x\)拆解成\(2^{ya} \cdot C\),那么要保证\(ya \geq p\)即\(x\)是\(2^{y}\)次的倍数。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int a, p;
ll mod;
ll qmod(ll base, ll n) {
ll res = 1;
while (n) {
if (n & 1) {
res = res * base % mod;
}
base = base * base % mod;
n >>= 1;
}
return res;
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d", &a, &p);
if (a & 1) {
puts("1");
continue;
}
mod = 1ll << p;
if (mod > 30) {
ll res = 0;
for (int i = 1; i <= p; ++i) {
if (qmod(a, i) == qmod(i, a)) {
++res;
}
}
ll remind = mod - p;
if (a >= p) {
printf("%lld\n", res + (remind + 1) / 2);
} else {
int t = (p / a) + (p % a != 0);
t = 1ll << t;
res += mod / t - p / t;
printf("%lld\n", res);
}
} else {
ll res = 0;
for (int i = 1; i <= mod; ++i) {
if (qmod(a, i) == qmod(i, a)) {
++res;
}
}
printf("%lld\n", res);
}
}
return 0;
}
L. Median
题意:
有\(n\)个人进行排队,有\(m\)对先后关系,问是否存在一个合法的拓扑序使得第\(i\)个在站在中间,保证\(n\)是奇数。
思路:
首先要判断是否是\(DAG\),如果不是,直接全\(0\)。
对每个数爆搜出小于它的数的个数\(x\)以及大于它的数的个数\(y\),然后判断是否\(x < n / 2\)并且\(y < n / 2\)。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
int n, m;
vector<int>G1[maxn], G2[maxn];
int du[maxn];
int up[maxn], down[maxn];
int vis[maxn];
int cnt;
void DFS1(int u,int fa) {
vis[u] = 1;
for (auto v : G2[u]) {
if(!vis[v]) {
cnt++;
DFS1(v, u);
}
}
}
void DFS2(int u,int fa) {
vis[u] = 1;
for (auto v : G1[u]) {
if(!vis[v]) {
cnt++;
DFS2(v, u);
}
}
}
bool Topo() {
cnt = 0;
queue<int>q;
for (int i = 1; i <= n; ++i) {
if(du[i] == 0) {
q.push(i);
}
}
while(!q.empty()) {
int u = q.front();
q.pop();
cnt++;
for (auto v : G1[u]) {
if(--du[v] == 0) {
q.push(v);
}
}
}
return cnt == n;
}
void Init() {
for (int i = 1; i <= n; ++i) {
G1[i].clear();
G2[i].clear();
du[i] = 0;
up[i] = 0;
down[i] = 0;
}
}
int main() {
int t;
scanf("%d", &t);
while(t--) {
scanf("%d %d", &n, &m);
Init();
for (int i = 1, u, v; i <= m; ++i) {
scanf("%d %d", &u, &v);
G1[u].push_back(v);
G2[v].push_back(u);
du[v]++;
}
if(!Topo()) {
for (int i = 1; i <= n; ++i) {
putchar('0');
}
putchar('\n');
continue;
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
vis[j] = 0;
}
cnt = 0;
DFS1(i, -1);
up[i] = cnt;
for (int j = 1; j <= n; ++j) {
vis[j] = 0;
}
cnt = 0;
DFS2(i, -1);
down[i] = cnt;
}
for (int i = 1; i <= n; ++i) {
if(up[i] < (n + 1) / 2 && down[i] < (n + 1) / 2) {
putchar('1');
} else {
putchar('0');
}
}
putchar('\n');
}
return 0;
}
M. Sekiro
签到题。
代码:
view code
#include <bits/stdc++.h>
using namespace std;
int main() {
int T; scanf("%d", &T);
while (T--) {
int n, k;
scanf("%d%d", &n, &k);
while (k-- && n > 1) {
n = (n + 1) / 2;
}
printf("%d\n", n);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号