DS AVL树详解
先说说二叉搜索树: 是有序的二叉树,根值>左节点值,右节点值>根值。
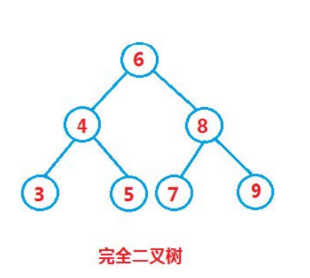
如果要查找某个值,二叉搜索树和二分查找一样,每进行一次值比较,就会减少一半的遍历区间。
但是,如果树插入的值一直递增/递减,就会出现这种情况:

这样,二叉树性能就完全失去了,直接退化成了顺序表,查找效率低下。
由此,引入了能保持性能最佳的二叉搜索树。
AVL树: 具有高度平衡的二叉搜索树。
性质: 1.它的左右子树都是AVL树
2.左右子树高度差(简称平衡因子)的绝对值不超过1
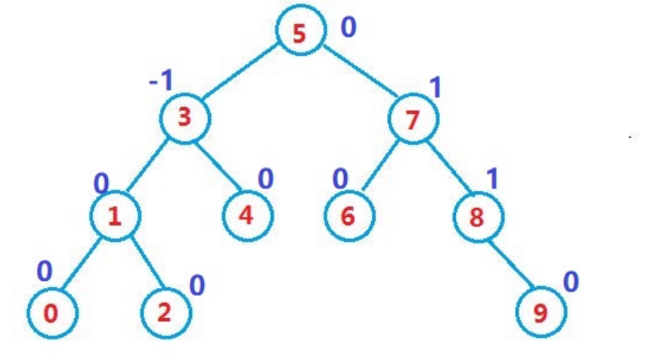
搜索的时间复杂度: O(log2(n))
AVL树节点
struct AVLTree{
pair<K,V> kv;
AVLTreeNode* left;
AVLTreeNode* right;
AVLTreeNode* parent;
int bf; //balance factor
};
与二叉搜索树不同的是引入了父节点(方便后面讲的旋转)和平衡因子(保持高度平衡的核心)。
AVL树的插入:
在插入节点后,需要调整平衡:
1.bf更新规则:新增在左 父亲bf-1 ; 新增在右 父亲bf+1
2.持续往祖先更新 如果 祖先bf==0,祖先肯定是从1或者-1变来的,那就说明祖先所在子树的高度不变,停止更新;
祖先|bf|==1,祖先肯定是从0变来的,说明祖先所在子树高度变了,继续往上更新;
祖先|bf|==2,祖先肯定是从1或者-1变来的,说明高度已经不平衡了,需要旋转调整;
旋转:
1.左单旋: 新结点插在较高右子树右侧 2 1
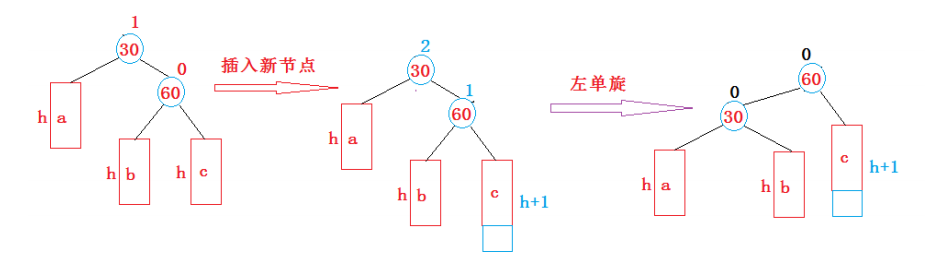
2.右单旋: 新结点插在较高左子树左侧 -2 -1

3.左右双旋(先左单旋parent,再右单旋g): 新结点插在较高左子树右侧 -2 1 -> -2 -2 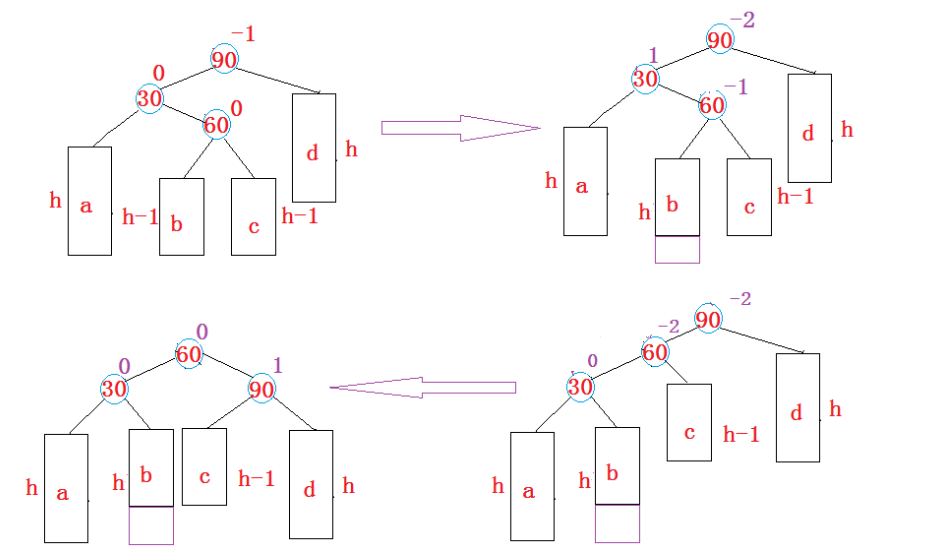
4.右左双旋: 新结点插在较高右子树左侧 2 -1 -> 2 2
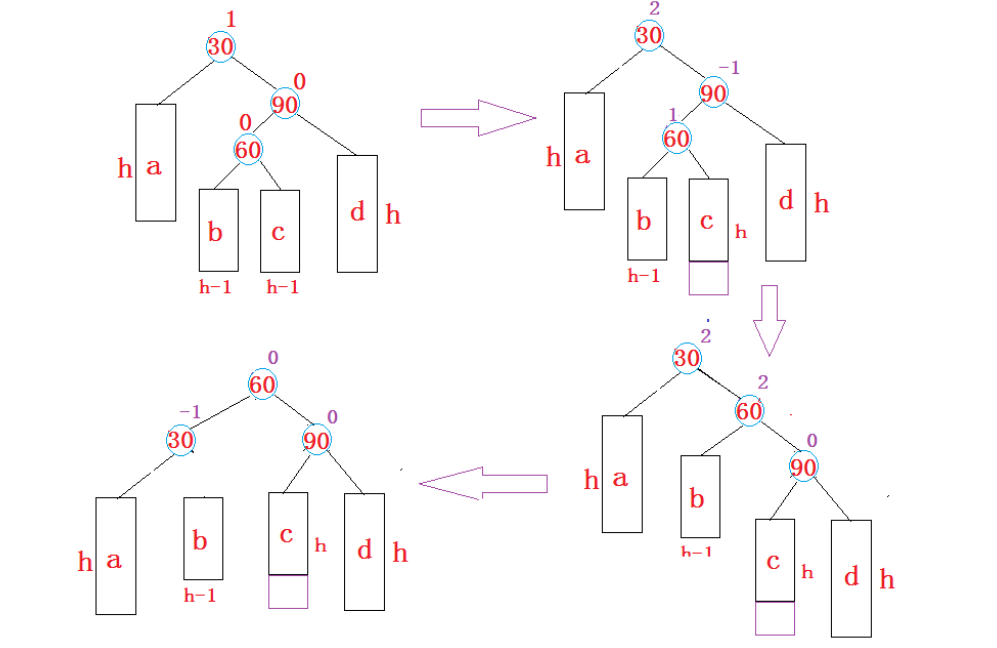
总结:
//右单旋
void RotateR(Node* parent)
{
Node* subL = parnet->left;
Node* subLR = subL->right;
//右旋下去,原根左孩子成为新根
parent->left = subLR;
if(subLR) //LR不为空,才连接其父亲
subLR->parent = parent;
//更新新根与原根的关系
subL->right = parent;
//记录原根的父
Node* ppNode = parent->parent;
//更新新根与原根的关系
parent->parent = subL;
//下面都是因为双向链表带来的问题
//更新原根父与新根的关系
//新根就是根节点
if(ppNode==nullptr)
{
root = subL;
root->parent = nullptr;
}
//新根更新与原根父的关系
else
{
if(ppNode->left==parent)
ppNode->left = subL;
else
ppNode->right = subL;
subL->parent = ppNode;
}
//根据上图,更新部分节点平衡因子
parent->bf = subL->bf = 0;
}
//左单旋同理
void RotateL(Node* parent);
//右左双旋
void RotateRL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
int bf = subRL->bf;
//右左双旋
RotateR(parent->right);
RotateL(parent);
//更新双旋后的bf
//由于单旋会将bf置0,而双旋有三种情况,需要记录旋转前的新根的bf
//1.新结点插入后,subRL的bf是0 --- 插入的节点就是subRL
if(bf == 0)
{
parent->bf = subRL->bf = subR->bf = 0;
}
//2.新结点插入后,subRL的bf是1 --- 插入的节点在subRL右边
else if(bf == 1)
{
subR->bf = 0;
parent->bf = -1;
subRL->bf = 0;
}
//3.新结点插入后,subRL的bf是-1 --- 插入的节点在它subRL左边
else if(bf == -1)
{
parent->bf = 0;
subR->bf = 1;
subRL->bf = 0;
}
}
//左右双旋同理
void RotateLR(Node* parnet);
AVL树插入代码
bool Insert(const pair<K,V>& kv)
{
//插入结点
if(root == nullptr)
{
root=new Node(kv);
root->bf = 0;
return true;
}
Node* parent = nullptr;
Node* cur = root;
while(cur)
{
if(cur->kv.first < kv.first)
else if(cur->kv.first > kv.first)
else
return false;
}
cur = new Node(kv);
//父节点连接插入的结点
if(parent->kv.first < kv.first)
{
parent->right = cur;
cur->parent = parent;
}
else
{
...
}
//调平衡
//1.新增在左 父亲bf-1 新增在右 父亲bf+1
//2.持续往祖先更新 if 祖先bf == 0,则祖先所在子树高度不变,停止往上更新
// if 祖先|bf| == 1,则祖先所在子树高度变了,继续往上更新
// if 祖先|bf| == 2,则祖先所在树不平衡,则旋转调整
//1.更新平衡因子
while(parent)
{
if(cur == parent->right)
parent->bf++;
else
parent->bf--;
//高度不变,更新完成
if(parent->bf == 0)
break;
//高度变了,继续更新
else if(abs(parent->bf) == 1)
{
cur = parent;
parent = parent->parent;
}
//不平衡,旋转调整
else if(abs(parent->bf) == 2)
{
//判断旋转方式
if(parent->bf==2)
{
if(cur->bf==1)
RotateL(parent);
else if(cur->bf==-1)
RotateRL(parent);
}
else if(parent->bf==-2)
{
if(cur->bf==-1)
RotateR(parent);
else if(cur->bf==1)
RotateLR(parent);
}
break;
}
else
assert(false);
}
}
因为引入了bf和双向链表,所以有了很多坑,应该避免以下两点:
1.单旋完成后,注意更新其新根与原根父节点的连接关系
2.双旋完成后,注意根据双旋规律进行bf更新


 浙公网安备 33010602011771号
浙公网安备 33010602011771号