题解 【AT4353 [ARC101D] Robots and Exits】

\(\large\mathcal{Description}\)

在一个数轴上有 \(n\) 个 \(\texttt{robot}\) 和 \(m\) 个 \(\texttt{exit}\).

每次操作可以把所有 \(\texttt{robot}\) 同时向左或向右移动 \(1\) 个单位长度，当一个 \(\texttt{robot}\) 遇到了一个 \(\texttt{exit}\), 它就会溜走。所有 \(\texttt{robot}\) 溜走之后停止操作。

求 \(\texttt{robot}\) 从 \(\texttt{exit}\) 溜走的方案数。两个方案不同，当且仅当存在至少一个 \(\texttt{robot}\) 从不同的 \(\texttt{exit}\) 溜走。

答案对 \(10^9+7\) 取模，\(n, m\le 10^5.\)

\(\large\mathcal{Solution}\)

首先我们可以不管比最左边 \(\texttt{exit}\) 还左边的 \(\texttt{robot}\), 因为它一定从最左边 \(\texttt{exit}\) 溜走，对答案没有影响。同理，我们也可以不管比最右边 \(\texttt{exit}\) 还右边的 \(\texttt{robot}\).

我们现在单独拎出一个 \(\texttt{robot}\) 进行研究。我们发现只有改变他向左或向右的最大值的操作才对这个 \(\texttt{robot}\) 有效果。所以我们如果把这个 \(\texttt{robot}\) 向左和向右的最大值作为一个平面坐标的两维的话，它的初始值是 \((0, 0)\), 然后不断地向上、向右延伸。

其实所有 \(\texttt{robot}\) 的曲线都长一个样对吧。

那一个 \(\texttt{robot}\) 何时溜走呢？是不是当他碰到了一个 \(\texttt{exit}\) 的时候。也就是说，我们设初始时第 \(i\) 个 \(\texttt{robot}\) 距离离它最近的两边的 \(\texttt{exit}\) 的距离分别是 \(a_i, b_i\). 然后这条曲线碰到 \(x=a_i\) 或 \(y=b_i\) 的时候它就推出历史的舞台了。

而且答案只取决于曲线先碰到 \(x=a_i\) 还是 \(y=b_i\).

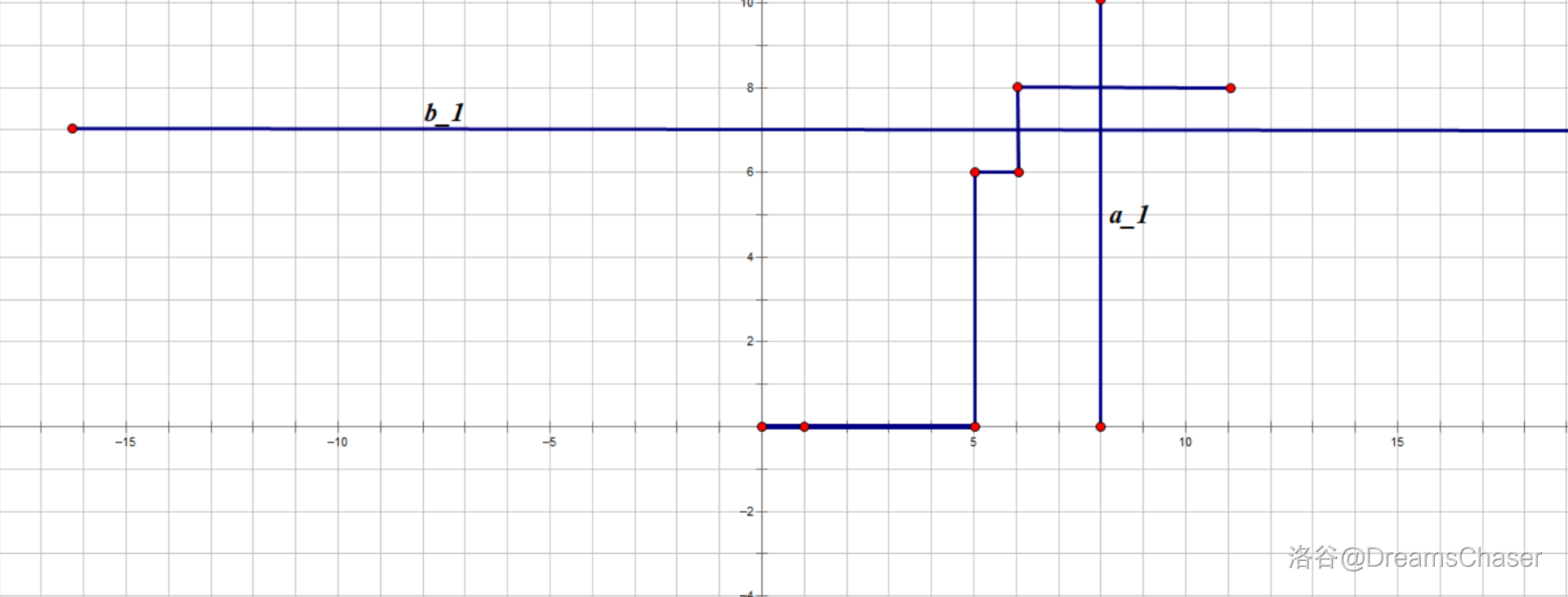
如果将 \(\texttt{robot}\) 的左标定义为 \((a_i-0.5, b_i-0.5)\). 那么所有在曲线左上方的 \(\texttt{robot}\) 都会从左侧的 \(\texttt{exit}\) 溜走，在曲线右下方的 \(\texttt{robot}\) 都会从右侧的 \(\texttt{exit}\) 溜走。

对于每个从右侧 \(\texttt{exit}\) 溜走的 \(\texttt{robot}\) 的集合, 容易构造出与之唯一对应的折线：

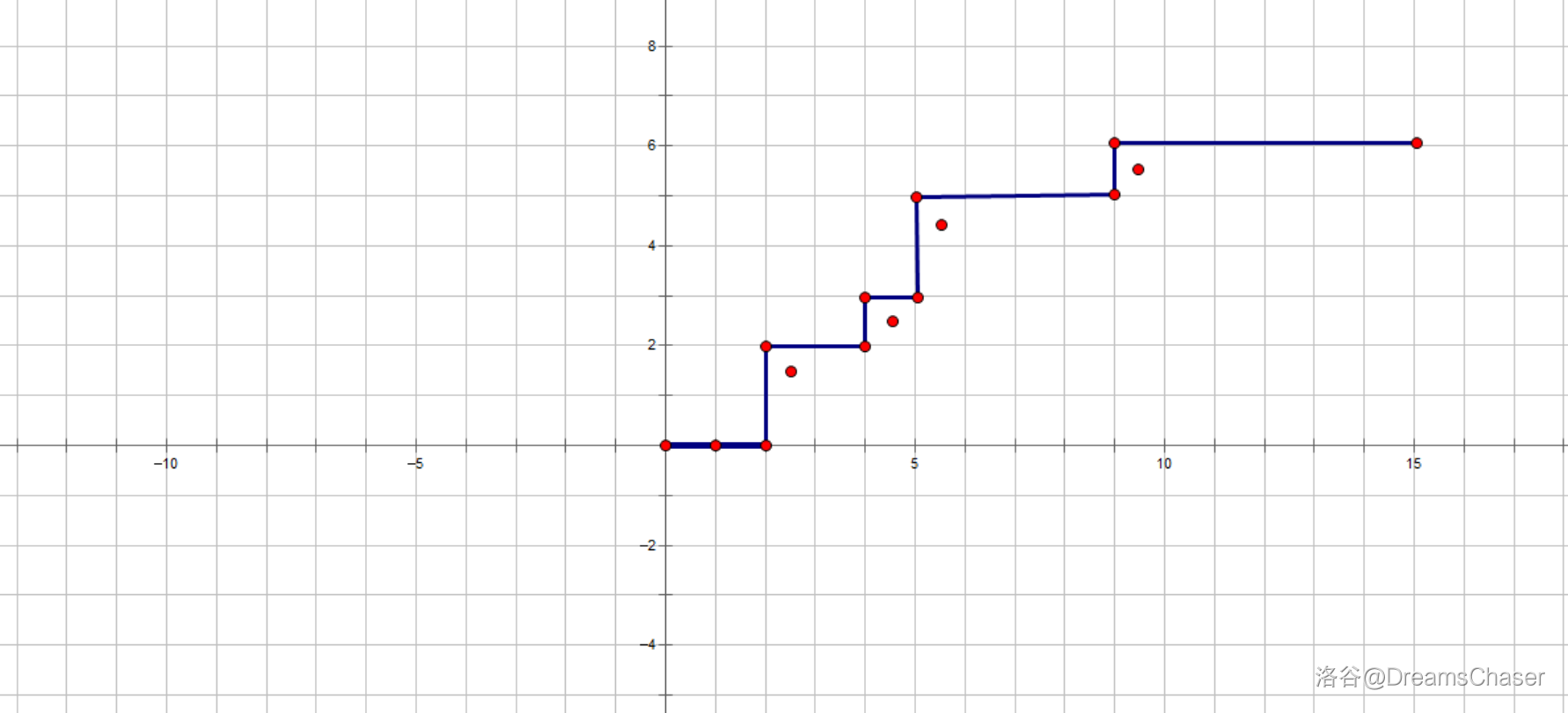
感性理解一下，就是卡在每个 \(\texttt{robot}\) （称为 \(\texttt{BR}\)）的直线。反之如果不能这样构造直线，我们也可以保证不存在直线使得这些 \(\texttt{robot}\) 都在右下方。

那么方案数就等于这样的直线的个数。令 \(f_i\) 表示延伸到第 \(i\) 个机器人且这是个 \(\texttt{BR}\). 转移方程显然：

\[f_i=\sum_{a_j<a_i,\ b_j<b_i}f_j+1 \]

然后这是一个 \(\mathcal{O}(n^2)\) 的转移式，显然是个二维偏序问题，用树状数组将其优化成 \(\mathcal{O}(n\log n)\).

\(\large\mathcal{Code}\)

const int N = 100010, mod = 1000000007;

int n, m, a[N], b[N], Max, dc[N];
pair<int, int> node[N];

struct BIT // 树状数组
{
    int c[N];
    void add(reg int x, reg int d) {for (; x <= Max; x += (x & (-x))) c[x] = (c[x] + d) % mod;}
    int ask(reg int x) {reg int sum = 0; for (; x; x -= (x & (-x))) sum = (sum + c[x]) % mod; return sum;}
} S;

int main()
{
    scanf("%d %d", &n, &m);
    for (reg int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
    for (reg int i = 1; i <= m; ++ i) scanf("%d", &b[i]);
    
    reg int tot = 0;
    for (reg int i = 1; i <= n; ++ i)
    {
        reg int pos = lower_bound(b + 1, b + m + 1, a[i]) - b;
        if (pos == 1 || pos > m) continue;
        node[ ++ tot] = make_pair(a[i] - b[pos - 1], - (b[pos] - a[i]));
        dc[tot] = -node[tot].second;
    }

    // 离散化
    
    sort(node + 1, node + tot + 1);
    for (reg int i = 1; i <= n; ++ i) node[i].second *= -1;
    sort(dc + 1, dc + tot + 1);
    Max = unique(dc + 1, dc + tot + 1) - dc;
    for (reg int i = 1; i <= tot; ++ i) node[i].second = lower_bound(dc + 1, dc + Max, node[i].second) - dc + 1;

    // DP
    
    S.add(1, 1);
    for (reg int i = 1; i <= tot; ++ i)
    {
        if (node[i].first == node[i - 1].first && node[i].second == node[i - 1].second) continue;
        reg int t = S.ask(node[i].second - 1);
        S.add(node[i].second, t);
    }
    
    printf("%d\n", S.ask(Max));
    
    return 0;
}