题解 【CF333D Characteristics of Rectangles】

\(\large\mathcal{Description}\)

\(\texttt{Gerald}\) 发现一个 \(n\) 行 \(m\) 列的表格。作为一个矩形表格的杰出专家，他立刻统计了表格的信息，即表格四个角数字的最小值。但是他并没有满足于最终结果：这个值太小了。为了让它更大，他准备对表格稍加修剪：删除左右的一些列，还有上下的几行。你需要找出在这样修剪后表格上述属性(即四角数字最小值)的最大值。请注意，在修剪后，表格要至少有 \(2\) 行 \(2\) 列。剪去的行和列数目可以为 \(0\).
\(n, m\le 1000\)

\(\large\mathcal{Solution}\)
首先这道题要求的是“最小值最大”，考虑到二分。
本题的关键点是：如何判断能否找到一个四个角都 \(\ge x\) 的矩形）？
考虑到一种打标记的思路，图示如下（黄色表示 \(\ge x\) 的数）：

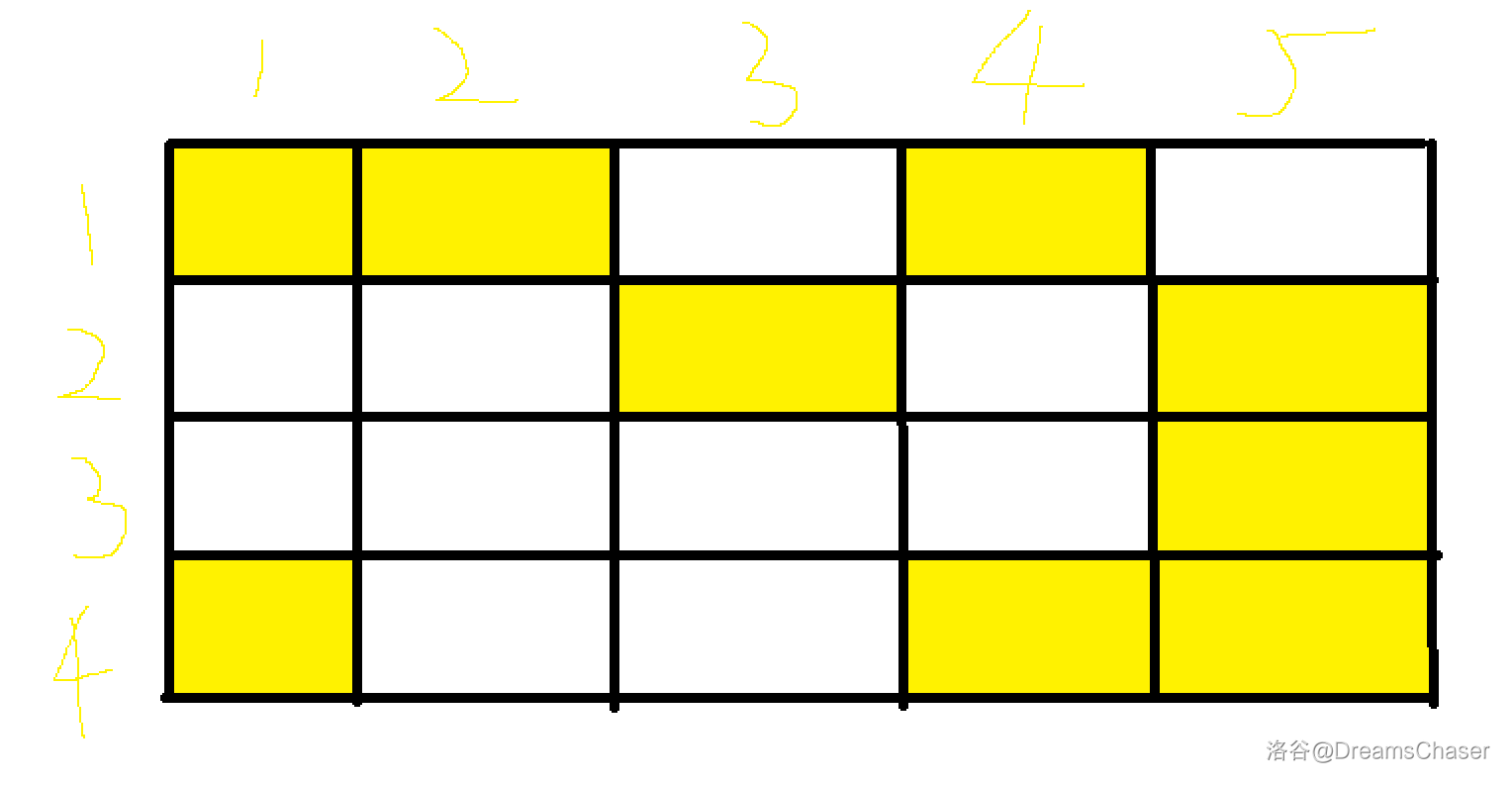
我们依次遍历这张图，例如：

• 遍历到第一行，发现 \(\text{1, 2, 4}\) 是黄色，我们将 \((1,2)(1,4)(2,4)\) 打上标记。
• 遍历到第二行，发现 \(\text{3, 5}\) 是黄色，我们将 \((3,5)\) 打上标记。
• 遍历到第三行，发现 \(\text{5}\) 是黄色，不做处理。
• 遍历到第四行，发现 \(\text{1, 4, 5}\) 是黄色，我们将 \((1,4)(1,5)(4,5)\) 打上标记。但 \((1,4)\) 在第一行以打上标记，这就说明：第一行的 \((1,4)\) 与第四行的 \((1,4)\) 均是黄色，那么我们就找到了一个四个角都 \(\ge x\) 的矩形。

简单来说：

• 我们遍历所有行
• 将所在行内为黄色的格子两两打上标记
• 如果打标记时找到了打过标记的点，那么就找到了一个四个角都 \(\ge x\) 的矩形。
• 否则找不到。

\(\large\mathcal{Code}\)

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int N = 1010;

int n, m, pla[N], vis[N][N];
LL val[N][N], l, r;

bool check(LL x)
{
    memset(vis, 0, sizeof vis);
    for (int i = 1; i <= n; i ++ )
    {
        int tmp = 0;
        for (int j = 1; j <= m; j ++ )
            if (x <= val[i][j])
                pla[ ++ tmp] = j;

        for (int j = 1; j <= tmp; j ++ )
            for (int k = 1; k < j; k ++ )
            {
                if (vis[pla[k]][pla[j]]) return true;
                else vis[pla[k]][pla[j]] = 1;
            }
    }
    return false;
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            scanf("%lld", &val[i][j]);
            r = max(r, val[i][j]);
        }

    while (l < r)
    {
        LL mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }

    printf("%lld\n", r);

    return 0;
}