20250903 S2模拟赛

A. 可爱精灵宝贝

Branimirko是一个对可爱精灵宝贝十分痴迷的玩家。最近，他闲得没事组织了一场捉精灵的游戏。游戏在一条街道上举行，街道上一侧有一排房子，从左到右房子标号由1到n。

刚开始玩家在k号房子前。有m个精灵，第i只精灵在第A[i]栋房子前，分值是B[i]，以及它在T[i]秒内（含）存在，之后消失。Branimirko可以选择移动至相邻的房子，耗时1秒。抓住精灵不需要时间，精灵被抓住后消失。时间从第1秒开始。Branimirko能最多获得多少分值和。
Input

输入的第1行为三个正整数n，k，m。

接下来m行描述精灵的信息，分别为A[i]，B[i]，T[i]。
Output

输出Branimirko能最多获得多少分值和。
Sample Input

10 5 4
1 30 4
3 5 7
7 10 12
9 100 23

Sample Output

115

100%的数据：k≤n≤1000,m≤100,A[i] ≤N,B[i] ≤100,T[i] ≤2000，所有数为正整数。

---

离散化之后就是关路灯

设f[l][r][t]为所用时间为t，经过了l~r，现在在r的最大分值，g[l][r][t]，类似，不过在l

预处理：离散化房屋编号

然后从l~r 向 l-1 ~ r或 l ~ r+1 转移

---

B. 多米诺

题目描述

大小双王对于多米诺有独特的理解。

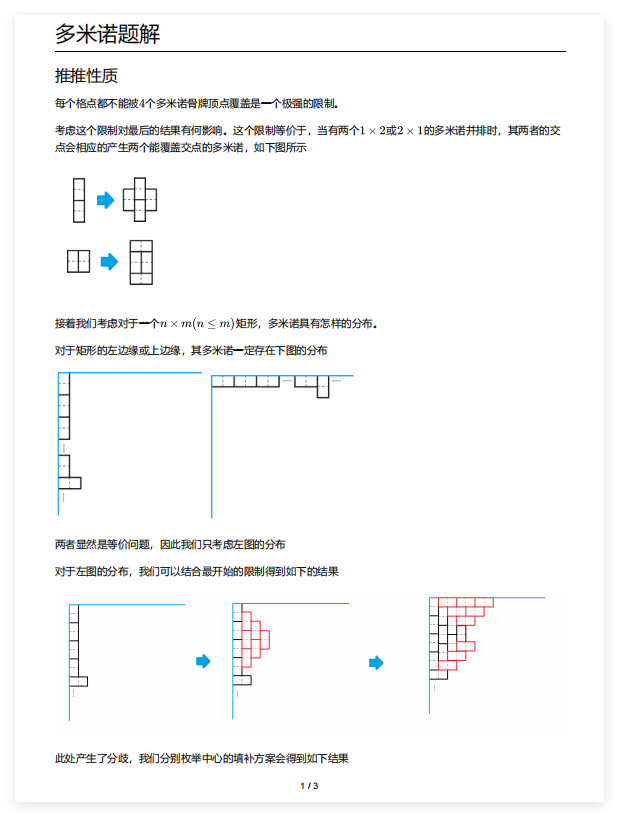
现在有一个 n×m 的格子大小的木板，大王想用 1×2 的多米诺骨牌把格子填满。大王不满足于普通的填法，大王还想让每个格点都不能被 4 个多米诺骨牌顶点覆盖。

大小双王想问你有多少个方案把他们填满呢。如果答案太大，对 998244353 取模。

同色为一块多米诺骨牌。图一二为一种合法的装填方案，图三不合法因为黄色点被 4 个多米诺骨牌顶点覆盖了
输入格式

一行两个整数 n,m，表示木板的大小。
输出格式

输出一行一个整数表示答案。
输入样例1

4 4

输出样例1

2

输入样例2

5 100

输出样例2

1050912

对于 100%100% 的数据，满足 1≤n,m≤10^7

---

n是1e7

看题解，说要转到1维，为什么一定是一维的

因为你考虑第一列（行同理），一定是若干个竖着的然后加一个横着的，否则会无法避免地出现非法情况。

然后横着的那个，你考虑如果没有在尽头结束（放在尽头），那么后面就填不满了（剩余奇数个格子）

所以结论就是一定是由若干个n*k的矩形填充的。

下面是官方题解。

---

C. 走迷宫

题目描述

大小双王在闯迷宫，尽快熟悉迷宫是一件很重要的事。大王想知道迷宫中有多少条通关的路径。

迷宫是一个 n×m 的网格，每个格子里面有一个数字。一条通关的路径是满足以下条件的路径：

1、大小双王只能走上下左右 4 个方向的相邻格子；

2、大小双王只能走相邻数字比当前格子大 2 的格子；

3、大小双王走的路径长度(走过的格子个数)必须至少为 4；

4、如果周围存在还能继续走的格子，大小双王只能继续走；

5、起点周围不存在比它恰好小 2 的格子。

1≤n,m≤1000, 保证迷宫里的数字绝对值不超过 2×10^6

---

设f[i][0/1/2/3/4]表示第i个点经过了0123大于等于4的方案数。

连边，建图，然后跑dagDP，拓扑排序转移

---

2≤n≤100000

---

由于题解两个NB的不等式

可以算出来上界

先枚举D

然后枚举两个等差数列的分界点（提前预处理每一个d的每一个前缀和后缀的答案，然后计算答案）

考虑使用对顶堆维护，即一个大根堆维护前1/3小的，一个小根堆维护2/3大的。

#include <iostream>
#include <vector>
#include <queue>
#include <numeric>
#include <algorithm>

using namespace std;

const long long INF = -1;

long long get_cost(long long c, long long x) {
    long long d = x - c;
    if (d < 0) {
        return -d;
    }
    if (d % 2 == 0) {
        return d / 2;
    }
    return (d + 3) / 2;
}

struct CostCalc {
    priority_queue<long long> l_q;
    priority_queue<long long, vector<long long>, greater<long long>> r_q;

    long long s_l = 0;
    long long s_r = 0;
    long long e_l = 0;
    long long o_l = 0;

    int get_l_size() const {
        long long k = l_q.size() + r_q.size();
        return (2 * k + 2) / 3;
    }

    void p_l(long long v) {
        l_q.push(v);
        s_l += v;
        if (v % 2 == 0) e_l++; else o_l++;
    }

    long long pop_l() {
        long long v = l_q.top();
        l_q.pop();
        s_l -= v;
        if (v % 2 == 0) e_l--; else o_l--;
        return v;
    }

    void p_r(long long v) {
        r_q.push(v);
        s_r += v;
    }

    long long pop_r() {
        long long v = r_q.top();
        r_q.pop();
        s_r -= v;
        return v;
    }

    void rebalance() {
        int t_s = get_l_size();
        while (l_q.size() < t_s && !r_q.empty()) {
            p_l(pop_r());
        }
        while (l_q.size() > t_s && !l_q.empty()) {
            p_r(pop_l());
        }
        if (!l_q.empty() && !r_q.empty() && l_q.top() > r_q.top()) {
            long long l_t = pop_l();
            long long r_t = pop_r();
            p_l(r_t);
            p_r(l_t);
        }
    }

    void add(long long v) {
        if (!l_q.empty() && v <= l_q.top()) {
            p_l(v);
        } else {
            p_r(v);
        }
        rebalance();
    }

    long long calc_cost(long long x) const {
        long long k_l = l_q.size();
        long long k_r = r_q.size();
        
        long long c_r = s_r - x * k_r;
        long long c_l = 0;
        long long c_p = x * k_l - s_l;
        
        long long c_diff;
        if (x % 2 == 0) {
            c_diff = o_l;
        } else {
            c_diff = e_l;
        }
        
        c_l = (c_p + 3 * c_diff) / 2;
        
        return c_l + c_r;
    }

    long long query_cost() const {
        if (l_q.empty() && r_q.empty()) return 0;
        if (l_q.empty()) {
            return calc_cost(r_q.top());
        }

        long long mc = l_q.top();
        long long c1 = calc_cost(mc);
        long long c2 = calc_cost(mc - 1);
        
        return min(c1, c2);
    }

    void clear() {
        while (!l_q.empty()) l_q.pop();
        while (!r_q.empty()) r_q.pop();
        s_l = s_r = 0;
        e_l = o_l = 0;
    }
};

void update_min(long long& min_c, long long new_c) {
    if (min_c == INF || new_c < min_c) {
        min_c = new_c;
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    if (!(cin >> n)) return 0;

    if (n <= 2) {
        cout << 0 << '\n';
        return 0;
    }

    vector<long long> a(n);
    long long m_a = 0;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        if (a[i] > m_a) m_a = a[i];
    }
    
    long long d_l = (m_a + n) / max(1, n - 1) + 5;

    long long min_c = INF;

    vector<long long> c(n);
    vector<long long> p_c(n);
    vector<long long> s_c(n);

    CostCalc p_d, s_d;

    for (long long d = -d_l; d <= d_l; d++) {
        for (int i = 0; i < n; i++) {
            c[i] = a[i] - (long long)i * d;
        }

        p_d.clear();
        for (int i = 0; i < n; i++) {
            p_d.add(c[i]);
            p_c[i] = p_d.query_cost();
        }

        s_d.clear();
        for (int i = n - 1; i >= 0; i--) {
            s_d.add(c[i]);
            s_c[i] = s_d.query_cost();
        }

        update_min(min_c, p_c[n - 1]);

        for (int i = 0; i < n - 1; i++) {
            update_min(min_c, p_c[i] + s_c[i + 1]);
        }
    }

    cout << min_c << '\n';

    return 0;
}