【题解】P7599 | 倍增 贪心 分类讨论

0.闲话

做不会的题，要么自己想，要么问一个人，不要同时问几个做法不同的人 / 看几篇做法不同的题解，这些可以等你 AC 后再看，效率会高很多。

总之还是感谢 L7_56 大佬讲解 %% ，虽然没听懂，但是自己磨出来了。

很多题解是 APIO 刚完的时候写的，故讲解不太仔细，在这里补充一下。

1.题目相关

简化题意：

一排树，高度互不相同，每次跳跃会跳到左边第一个比它高的点，或右边第一个比它高的点，多次询问从 $[A,B]$ 中任意点到 $[C,D]$ 中任意点的最少步数，强制在线。

数据范围：

$n,q \leq 2\times 10^5$

原题:

lougu P7599

2.约定与记号

本文对树的编号从1开始，在开始和结尾放两棵无限高的树不影响答案。

$H_i$ 表示 $i$ 的高度 ， $L_i$ 表示 $i$ 左边第一个比它高的点 ， $R_i$ 表示 $i$ 右边第一个比它高的点 。

约定 $max[A,B]$ 本文中表示 $\max_{i\in[A,B]}H_i$ ， $min[A,B]$ 本文中表示 $\min_{i\in[A,B]}H_i$

特别地， $L_0=R_0=0\ ,\ L_{n+1}=R_{n+1}=n+1\ ,\ H_0=N_{n+1}= +\infty$

---

3.算法，思维过程

首先有 $O(nq)$ $\text{BFS}$ ，与正解没啥关系，故不讨论。

1.$\text{A=B,C=D}$

观察特殊数据，考虑对于 $A=B,C=D$ 的特殊数据，思考如何处理。

首先，有解的充要条件是 $max[A,C-1] \leq H_C$ ， 若不满足，一定会经过 高度为 $max[A,C-1]$ 的这个点 且无法到达 $C$ , 否则一直向右跳则有解。

若有目前在 点 $i (i\leq C)$ , $H_{L_i} \leq H_C, H_{R_i}\leq H_C$ ， 则跳到 $Li,Ri$ 中高度更高的点不会更劣。

证明是显然的 ， 较低者能跳到的两个边界其中之一是较高者，另一边是 $p$ , 较高者的两个边界之一为 $p$ ，另一边界显然不会更小。

所以一定是会从起点开始，不断向 $Li,Ri$ 中高度更高的点跳跃，直到两者中较高者高度大于等于终点高度。

接下来的最优决策就是一直向右跳，

若 $R_i$ 大于等于终点高度，又因为有解的条件，此时 $R_i$ 显然是终点

若 $L_i$ 大于等于终点高度（此时显然是大于） ， 那么就显然一直向右跳，一定也是满足在不超过终点的高度跳尽可能高。

使用两次倍增 （一次跳尽可能高的点 ， 一次跳尽可能右的点 ） 即可解决 。

即 $Rt[i][x]$ 表示从 $i$ 向右开始跳 $2^x$ 步 , $Up[i][x]$ 表示从 $i$ 向尽可能高跳 $2^x$ 步 ， 然后常规倍增。

---

2.$\text{C=D}$

先只考虑有解的情况，即 $max[B,C-1] \leq max[C,D]$

接下来考虑起点的选择 ， 令 $[B,C)$ 中最大值的位置为 $p$ ，若 $p=B$ 则可以从 $p$ 一步走过去 , 否咋选择一个满足 $1$ 中的条件的一个最高的点 $x$ 作为起点，由于前部分是尽可能向上走，同 $1$ 中的证明，选择高的很明显不劣。

这个点就是 $[max\{Lp+1,A\} , B]$ 中的最大值 ， 因为有解且 $[Lp+1,p]$ 中的点都是符合条件的。

---

3.一般情况

一个特殊的值是 $[B,C-1]$ 中的最大值所在点p ， 分两种情况进行考虑 ， 经过它，不经过。

3.1 经过它

选择 $[max\{Lp+1,A\} , B]$ 中的最大值走过去，同 2 即可 ， 走到 $p$ 后一步即可走到。

3.2 不经过它

不经过 $p$ 那么就一定经过 $p$ 左边的某个比它大的点 ， 这种情况必须满足 $R_{L_p} \in[C,D]$ ， 显然 $R_{L_p}\geq C$ 。

反证：若 $R_{L_p} >D$ ， 因为不经过 p ， 显然是从 $p$ 左边的某个比 $p$ 大的点走过去 ， 此时 $L_p$ 是不能到达 $[C,D]$ 的 ， $L_p$ 左边的低于 $L_p$ 的要么经过 $L_p$ ， 要么只会走到高于 $L_p$ 的点 $q$ ， $R_q \geq R_{L_p} > D$ 所以一定满足条件。

若不满足条件，则必须经过 $p$

若 $L_p\in[A,B]$ 则可以一步走到 $R_{L_p}$

否则选取 $[A,B]$ 中的最大值向 $L_p$ 跳即可，然后一步跳到终点区间。

常规倍增(同 1 )即可，见配图。

---

配图：

无解

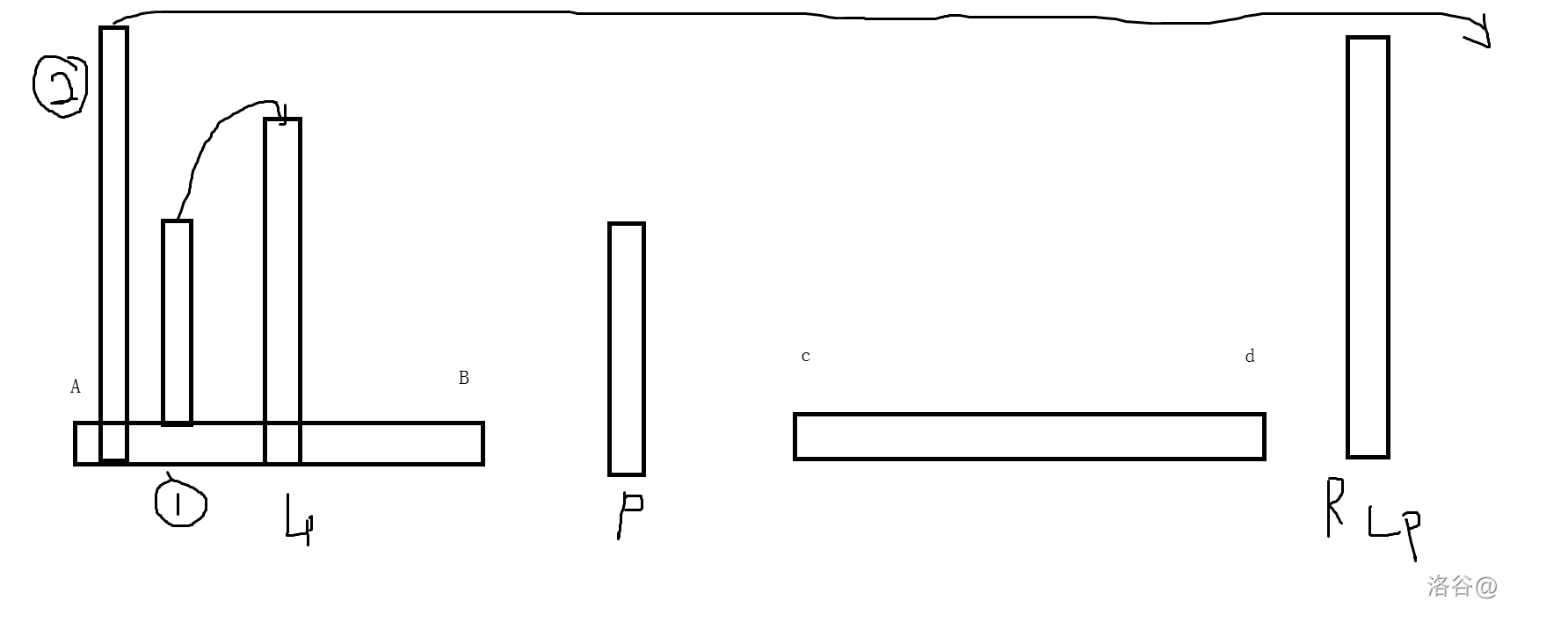
1 这种经过 $L_p$ 的路径不行。

2 这种高于 $L_p$ 的点的 $R$ 不会更靠左。

两种路径

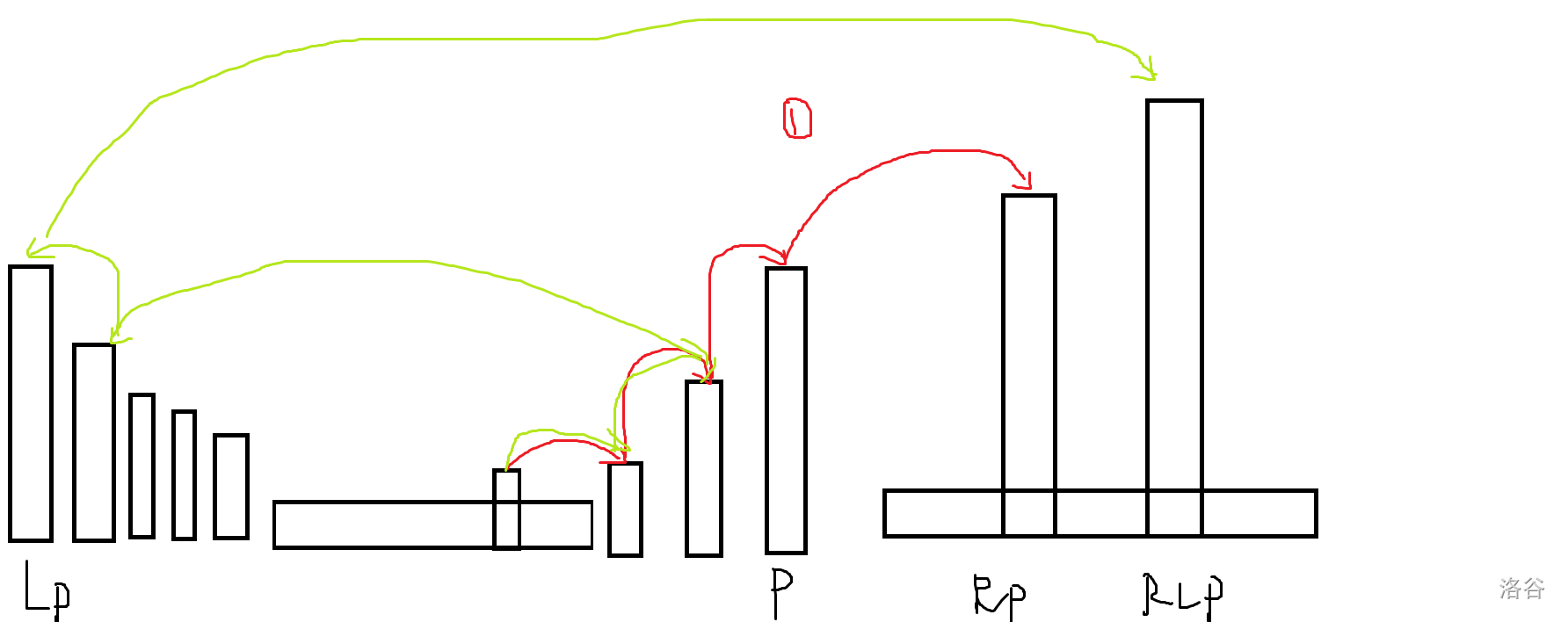
1 经过 $p$
2 不经过 $p$

使用倍增进行“跳”， ST 表进行 RMQ 查询 ， 时空复杂度 $O(n \log n)$ 。

---

4.代码实现

关键部分

/*分情况，特判*/

int minimum_jumps(int A, int B, int C, int D) {
    A++,B++,C++,D++;
    if(mx(B,C-1).first>mx(C,D).first) return -1;
    /*判掉无解*/
    auto mx1 = mx(B,C-1);
    if(mx1.second == B) return 1 ;
    int p = mx1.second , Lp = l[p] ,res = 1e9 + 100 ;
    /*过p*/
    int st = mx(max(A,Lp + 1) , B).second ; 
    res = min(res , calc1(st , p) + 1);
    /*到 R[l[p]]*/
    if(r[Lp]>=C&&r[Lp]<=D) {
        if(Lp>=A) res = min(res , 1);
        else res = min(res , calc2(mx(A,B).second,Lp) + 1) ; 
    }
    if(res >= 50000000) return -1;
    return res; 
}

/*两个倍增*/
int calc1(int st,int ed) {
    int ret = 0 ; 
    if(mx(st,ed-1).first > h[ed]) return 110000000 ;
    for(int i = Lg - 1 ; i >= 0 ; -- i) {
        if(h[Up[i][st]]>h[ed]) continue;
        st = Up[i][st] , ret += (1 << i) ;
    }
    debug(st) ; 
    for(int i = Lg - 1 ; i >= 0; -- i) {
        if(Rt[i][st] <= ed && Rt[i][st]) st = Rt[i][st] , ret += (1<<i);
    }
    if(st == ed)return ret;
    return 110000000;
}
int calc2 (int st,int ed) {
    int ret = 0 ;
    if(mx(ed+1,st).first > h[ed]) return 110000000 ;
    for(int i = Lg - 1 ; i >= 0 ; -- i) {
        if(h[Up[i][st]]>h[ed]) continue;
        st = Up[i][st] , ret += (1 << i) ;
    }
    for(int i = Lg - 1 ; i >= 0 ; -- i) {
        if(Lf[i][st] >= ed && Lf[i][st]) st = Lf[i][st] , ret += (1<<i) ; 
    }
    if(st == ed)return ret;
    return 110000000;
}

完整代码

-传送门-