START:
2021-08-15
17:10:14
题目链接:
方格取数:https://www.acwing.com/problem/content/1029/
传纸条:https://www.acwing.com/problem/content/description/277/
我们先来看第一题方格取数,它会是第二题的根基。
题目详情:
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
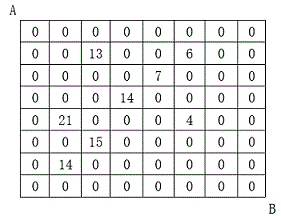
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
输入格式
第一行为一个整数N,表示 N×N 的方格图。
接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。
行和列编号从 1 开始。
一行“0 0 0”表示结束。
输出格式
输出一个整数,表示两条路径上取得的最大的和。
数据范围
N≤10N≤10
输入样例:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例:
67
我们先将信息预处理了:
#include<iostream>
using namespace std;
const int N=15;
int n;
int map[N][N];
int dp[2*N][N][N];
void solve(){
}
int main()
{
cin>>n;
int a,b,c;
while(cin>>a>>b>>c,a||b||c)map[a][b]=c;
solve();
return 0;
}
分析:
对于《方格取数》这个题目,如果我们分两次从(1,1)到(n,n)分别求局部最优解,
但是这样不可取,因为我们第一次走完之后,产生的结果会对
第二次的取值产生影响,所以不能分开求。
那么我们就两次取数同时开始,定义数组dp[N][N][N],
dp[k][i1][i2]表示第一次的路径从(1,1)走到(i1,k-i1)以及第二次的路径从(1,1)走到(i2,k-i2)
所能取到的最大的数字和。
其中dp[k][i1][i2]表示:k=i1+i2,在k==n+n的时候就是到达了终点,
i1表示第一次取数走到了第i1行,根据k==i1+j1,j1=k-i1,说明第一次取数走到了(i1,j1)==>(i1,k-i1),
同理,i2表示第二次取数的路径到达了(i2,j2)==>(i2,k-i2),
我们来推算dp[k][i1][i2]的动态转移方程:
我们可以怎样到达dp[k][i1][i2]?
我们画图来说明:
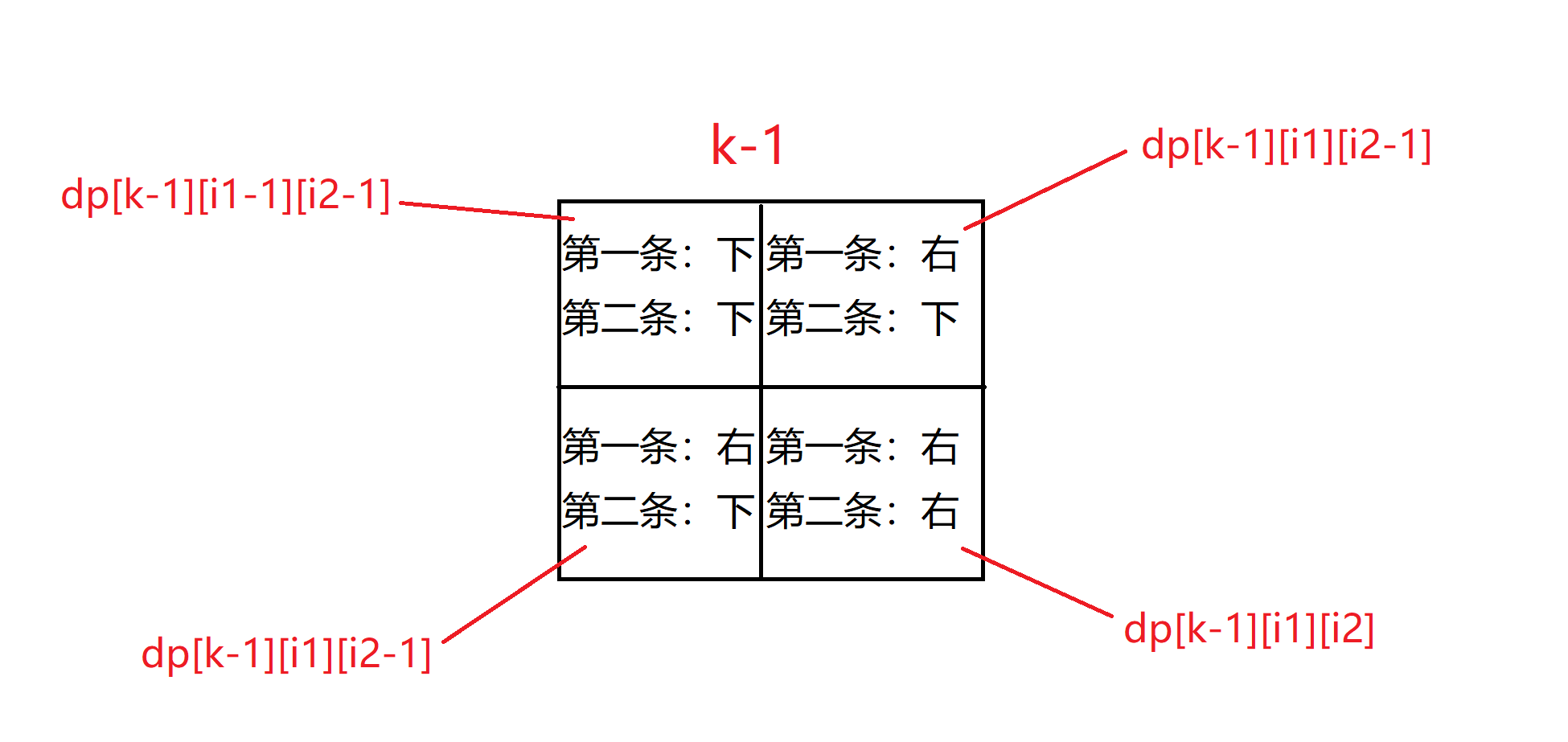
以上一共有四种状态可以到大dp[k][i1][i2],所以我们在这四种情况中取max。
当i1==i2时,(i1,j1)==(i2,j2),而题目说当某次取走某个点的数之后,这个点就变成了0,所以当我们的路径重叠时,我们只能加一次这个点
所以我们在循环里面要if判断
写核心函数solve(){}:
void solve(){
for(int k=2;k<=2*n;k++){
for(int i1=1;i1<=n;i1++){
for(int i2=1;i2<=n;i2++){
int j1=k-i1,j2=k-i2;
if(1<=i1&&i1<=n&&1<=i2&&i2<=n){
int &x=dp[k][i1][i2];
int t=map[i1][j1];
if(i1!=i2)t+=map[i2][j2];
x=max(x,dp[k-1][i1-1][i2-1]);
x=max(x,dp[k-1][i1-1][i2]);
x=max(x,dp[k-1][i1][i2-1]);
x=max(x,dp[k-1][i1][i2]);
x+=t;
}
}
}
}
cout<<dp[2*n][n][n]<<endl;
}
上面代码里面标红的语句,&x=dp[k][i1][i2]表示x是dp[k][i1][i2]的一个别名,x就是dp[k][i1][i2]。
#include<iostream>
using namespace std;
const int N=15;
int n;
int map[N][N];
int dp[2*N][N][N];
void solve(){
for(int k=2;k<=2*n;k++){
for(int i1=1;i1<=n;i1++){
for(int i2=1;i2<=n;i2++){
int j1=k-i1,j2=k-i2;
if(1<=i1&&i1<=n&&1<=i2&&i2<=n){
int &x=dp[k][i1][i2];
int t=map[i1][j1];
if(i1!=i2)t+=map[i2][j2];
x=max(x,dp[k-1][i1-1][i2-1]);
x=max(x,dp[k-1][i1-1][i2]);
x=max(x,dp[k-1][i1][i2-1]);
x=max(x,dp[k-1][i1][i2]);
x+=t;
}
}
}
}
cout<<dp[2*n][n][n]<<endl;
}
int main()
{
cin>>n;
int a,b,c;
while(cin>>a>>b>>c,a||b||c)map[a][b]=c;
solve();
return 0;
}
好!
我们现在解决了第一题《方格取数》,让我们来看看第二题《传纸条》,
题目详情:
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 m 行 n 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 (1,1),小轩坐在矩阵的右下角,坐标 (m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0 表示),可以用一个 0∼100 的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 2 个用空格隔开的整数 m 和 n,表示学生矩阵有 m 行 n 列。
接下来的 m 行是一个 m×n 的矩阵,矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度,每行的 n 个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1≤n,m≤50
输入样例:
3 3
0 3 9
2 8 5
5 7 0
输出样例:
34
我们先写好基础架构:
#include<iostream>
using namespace std;
const int N=55;
int n,m;
int map[N][N];
int dp[2*N][N][N];
void solve(){
}
int main()
{
cin>>m>>n;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)cin>>map[i][j];
solve();
return 0;
}
然后我们尽量将这道题向《方格取数》靠近,我们能看出,《传纸条》和《方格取数》就差一个条件:每个点只能遍历一次
但是我们可以证明:可以使用《方格取数》的思路来求解《传纸条》
证明:
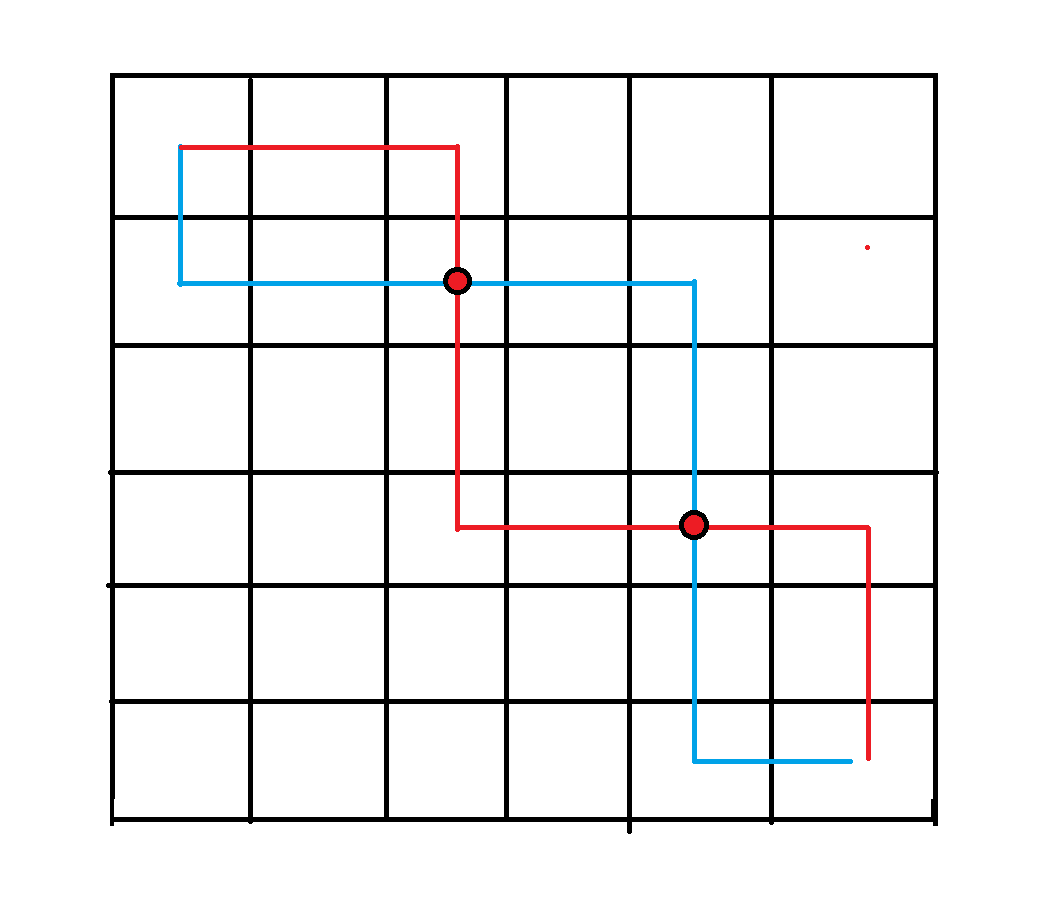
假设:利用题一的算法求得的最优路径如图所示,有多个重合点,但是《传纸条》这个题目里面,每个点只能遍历一遍,所以当两个点重合时,
有一个路径的点是0,是没有做出贡献的,并且两次路径是不能重合的,也就是说,总有一条路径在另一条路径的上方且不重合,如图所示的两条路径相交了,我们怎么办呢?在不改变最终结果的情况下将一条路径全部变到另一条路径上方,我们可以这样:
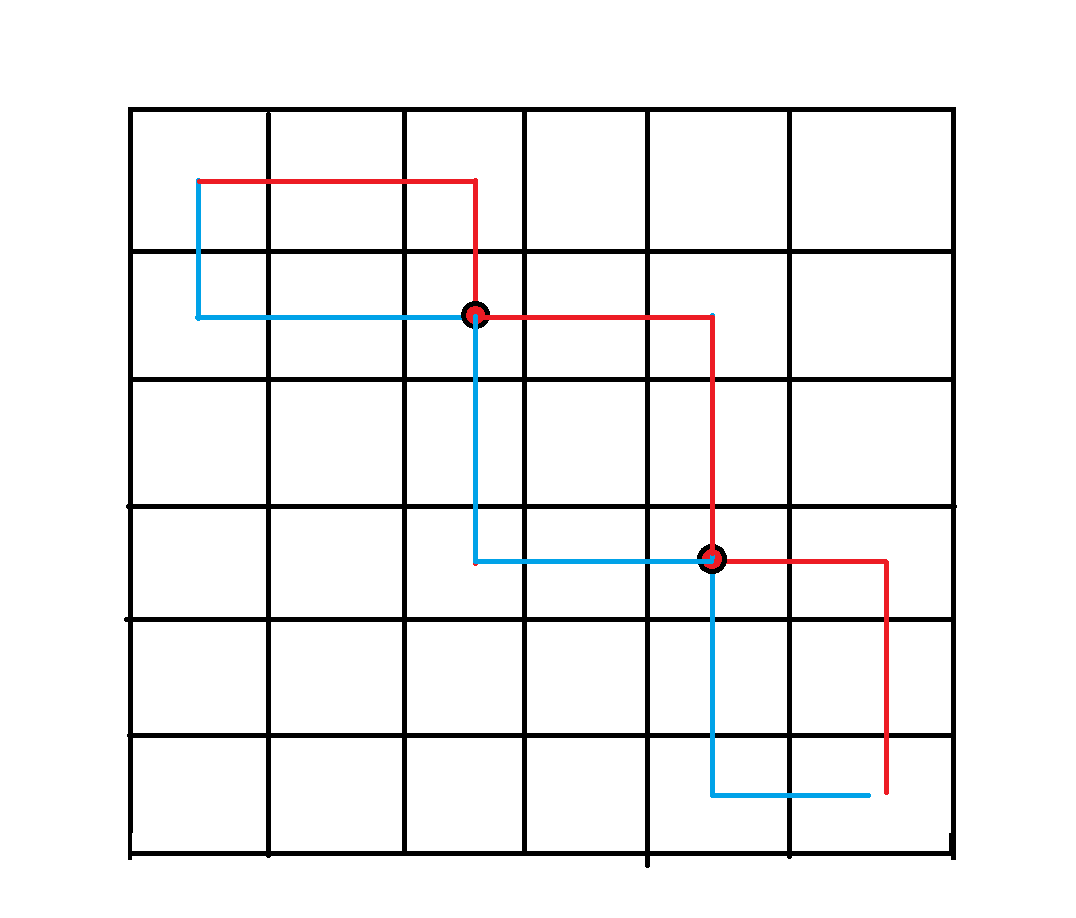
这样,我们就可以将一条路径全部变到另一条边的上方,处理完这些后,我们要处理路径重合的问题:
像上图的(2,3),(4,5)点就是重合点,我们知道,每个点只能遍历一遍,第二次就相当于没用,贡献为0,那么这条路径一定不是最优路径,因为我们可以从重合点的旁边绕过去,因为重合点第二次遍历的时候贡献为0,而我们从旁边绕过去的话贡献不为0,所以有重合点的路径一定不是最优路径,我们可以从重合点的两旁绕过去,如下图:
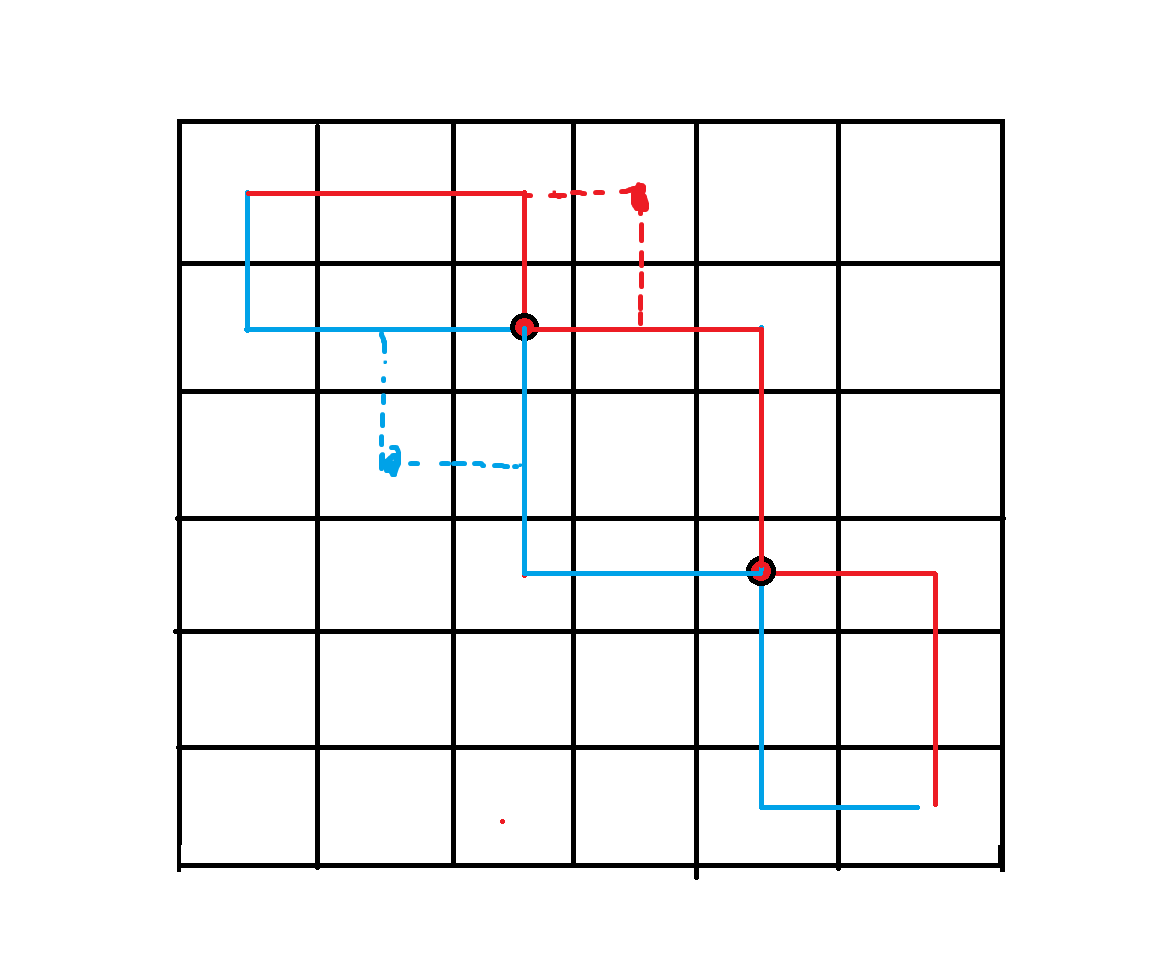
我们可以像上图一样,从重合点的两边选一边绕过去,所以最优路径一定是不重叠的,性质和《方格取数》是一样的,《方格取数》的最优路径也是不重叠的,所以我们可以使用《方格取数》的结构和代码来求解《传纸条》。
上代码!
#include<iostream>
using namespace std;
const int N=55;
int n,m;
int map[N][N];
int dp[2*N][N][N];
void solve(){
for(int k=2;k<=n+m;k++){
for(int i1=1;i1<k;i1++){
for(int i2=1;i2<k;i2++){
int j1=k-i1,j2=k-i2;
if(1<=i1&&i1<=m&&1<=i2&&i2<=m){
int t=map[i1][j1];
if(i1!=i2)t+=map[i2][j2];
int &x=dp[k][i1][i2];
x=max(x,dp[k-1][i1-1][i2-1]);
x=max(x,dp[k-1][i1][i2-1]);
x=max(x,dp[k-1][i1-1][i2]);
x=max(x,dp[k-1][i1][i2]);
x+=t;
}
}
}
}
cout<<dp[n+m][m][m]<<endl;
}
int main()
{
cin>>m>>n;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)cin>>map[i][j];
solve();
return 0;
}
END:
2021-08-15
20:43:27



 浙公网安备 33010602011771号
浙公网安备 33010602011771号