攻防世界|easy_RSA|

介绍一下RSA

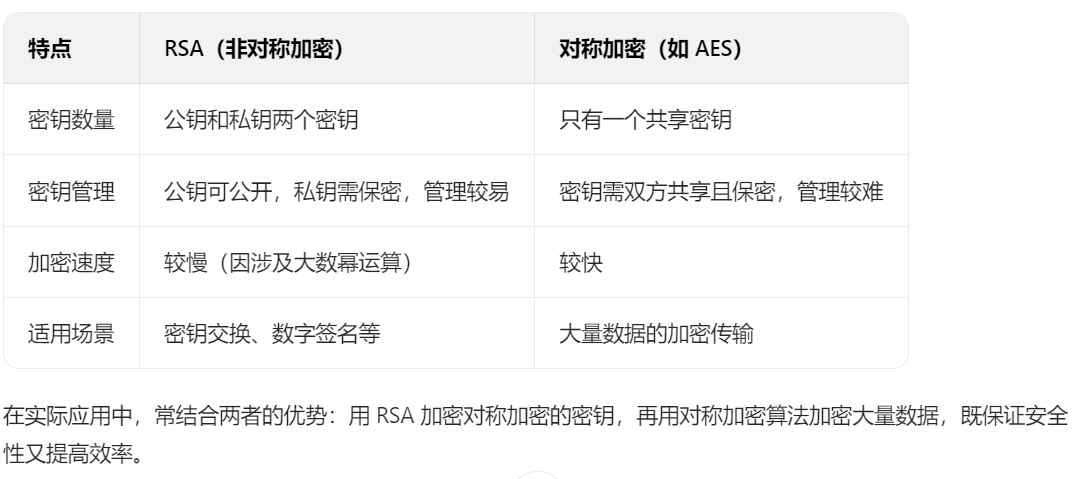
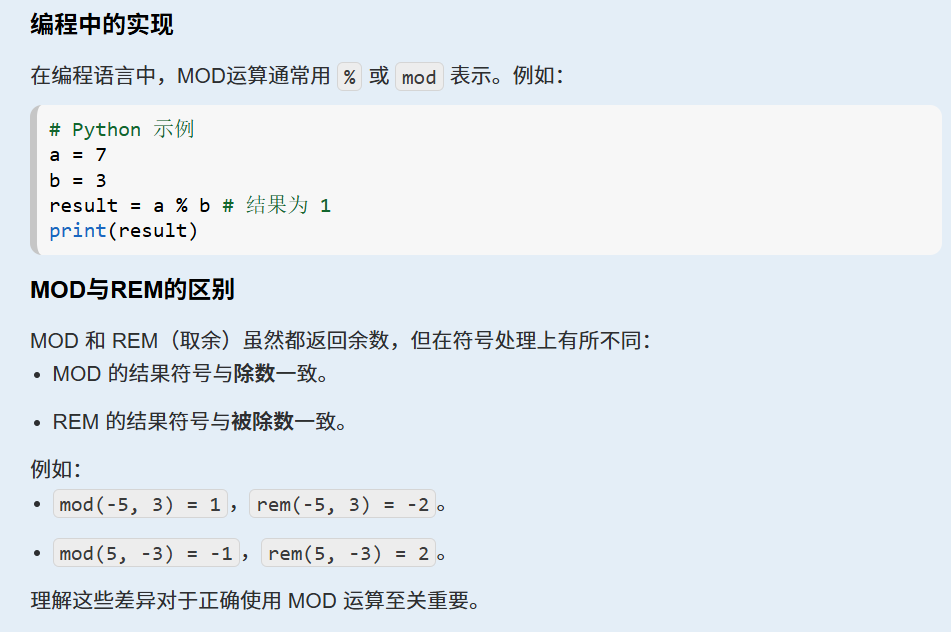
mod运算

欧拉函数ϕ(n)

φ(n) = (p-1)*(q-1) (这真是欧拉的一个伟大的发明)

解题

代码如下：

点击查看代码

def extended_gcd(a, b):
    """扩展欧几里得算法，返回(gcd(a,b), x, y)，其中ax + by = gcd(a,b)"""
    if b == 0:
        return (a, 1, 0)
    else:
        g, x, y = extended_gcd(b, a % b)
        return (g, y, x - (a // b) * y)

def mod_inverse(a, m):
    """计算a在模m下的逆元，若不存在返回None"""
    g, x, y = extended_gcd(a, m)
    if g != 1:
        return None  # 逆元不存在
    else:
        return x % m  # 确保结果为正数

# 已知参数
p = 473398607161
q = 4511491
e = 17

# 计算欧拉函数φ(n) = (p-1)*(q-1)
phi = (p - 1) * (q - 1)

# 计算d，即e模phi的逆元
d = mod_inverse(e, phi)

cyberpeace{125631357777427553}