BUAA_OO第一单元总结
BUAA_OO第一单元总结
程序结构分析
(注:类图将set和get方法省略)
第一次作业
类图
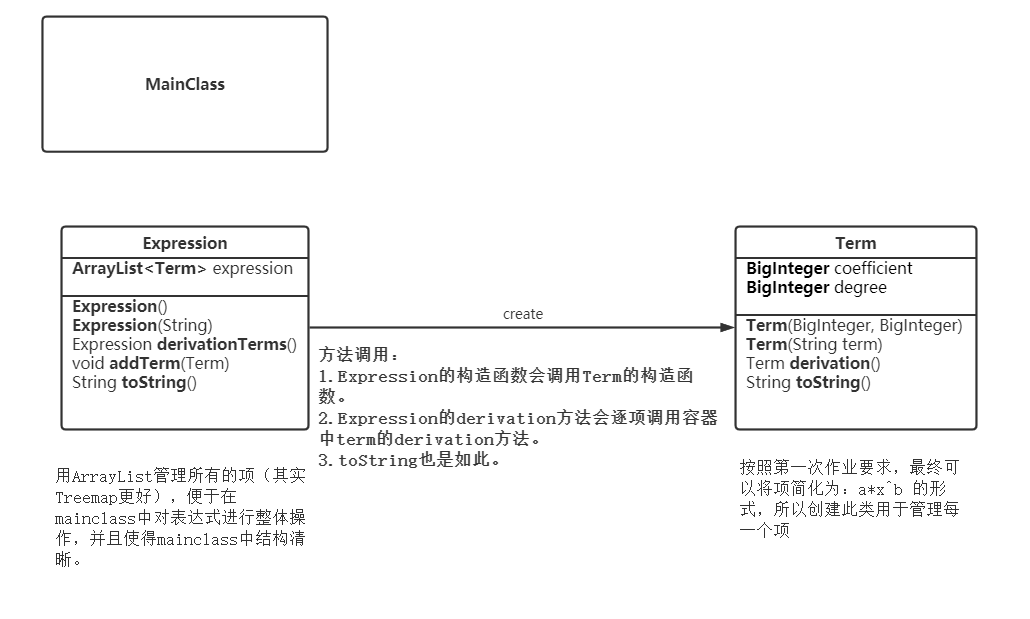
类与方法的评估
| 类/特征 | 类的规模 | 属性个数 | 方法个数 | 方法规模 | 方法分支数目 |
|---|---|---|---|---|---|
| MainClass | 11 | 0 | 1 | 6 | 无 |
| Expression | 93 | 1 | 5 | 大多数不超过20,最大40 | 较少 |
| Term | 93 | 2 | 8 | 最大30 | 较多 |
复杂度分析
类的复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Expression | 3.2 | 5 | 16 |
| MainClass | 1 | 1 | 1 |
| Term | 2.56 | 8 | 23 |
Expression中的OCavg(平均循环复杂度)标红,主要是toString中要遍历整个Arraylist调用Term的toString导致的,暂时没有方法来替换。
方法的复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Expression.Expression() | 0 | 1 | 1 | 1 |
| Expression.Expression(String) | 8 | 1 | 5 | 5 |
| Expression.addTerm(Term) | 3 | 3 | 3 | 3 |
| Expression.derivationTerms() | 1 | 1 | 2 | 2 |
| Expression.toString() | 10 | 2 | 4 | 5 |
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| Term.Term(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| Term.Term(String) | 21 | 1 | 8 | 8 |
| Term.compareTo(Term) | 0 | 1 | 1 | 1 |
| Term.derivation() | 0 | 1 | 1 | 1 |
| Term.getCoefficient() | 0 | 1 | 1 | 1 |
| Term.getDegree() | 0 | 1 | 1 | 1 |
| Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| Term.setDegree(BigInteger) | 0 | 1 | 1 | 1 |
| Term.toString() | 11 | 8 | 11 | 11 |
较高的部分主要在于:
①term的构造函数中需要用正则表达式来循环获取因子,最终将一个项存储起来。
②因为term的toString要优化,所以存在许多特判情况,不能简单输出为“a*x**b”。
自我评价
优点
结构简单
缺点
不具拓展性。因为在字符串处理环节,我是通过replace处理符号使得项与项之间都以“+”相隔,在后续的作业中不能对表达式因子做出反应,所以拓展性方面没有考虑全面。
第二次作业
类图
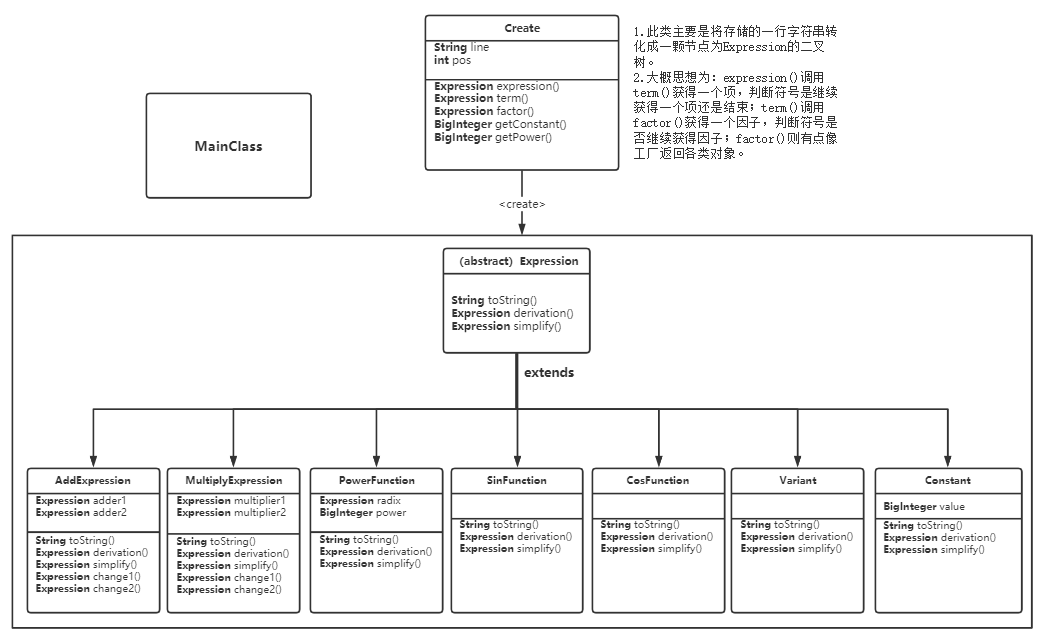
类与方法的评估
| 类/特征 | 类的规模 | 属性个数 | 方法个数 | 方法规模 | 方法分支数目 |
|---|---|---|---|---|---|
| MainClass | 19 | 0 | 1 | 15 | 无 |
| Create | 93 | 2 | 6 | 众数20左右,最大40 | factor()较多 |
| Expression | 8 | 0 | 3 | 无(抽象类) | 无(抽象类) |
| Constant | 25 | 1 | 5 | 1 | 无 |
| Variant | 15 | 0 | 3 | 1 | 无 |
| SinFunction | 13 | 0 | 3 | 1 | 无 |
| CosFunction | 15 | 0 | 3 | 1 | 无 |
| AddExpression | 119 | 2 | 6 | 有3个接近35 | 多 |
| MultiplyExpression | 120 | 2 | 8 | 有3个接近35 | 多 |
| PowerFunction | 47 | 2 | 6 | 众数10 | 较少 |
复杂度分析
类的复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| AddExpression | 3.83 | 10 | 23 |
| Constant | 1 | 1 | 5 |
| CosFunction | 1 | 1 | 3 |
| Create | 3.17 | 7 | 19 |
| Expression | n/a | n/a | 0 |
| MainClass | 1 | 1 | 1 |
| MultiplyExpression | 3.12 | 12 | 25 |
| PowerFunction | 1.67 | 4 | 10 |
| SinFunction | 1 | 1 | 3 |
| Variant | 1 | 1 | 3 |
OCavg(平均循环复杂度)较高主要是两方面:
①因为我存的数据结构类似二叉树结构,所以在长度优化的时候,AddExpression和MultiplyExpression需要先调用两个加式(或者乘式)的simplify方法,有点像树的遍历,可能导致了循环复杂度较高。
②Create中使用了递归下降读取字符串,三个方法互相调用:expression()调用term()获得项,term()调用factor()获得因子,最后的factor()则有点类似工厂模式:根据读取的因子类型返回不同类的对象。
方法的复杂度
(注:主要截取了存在主要方法的类)
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| AddExpression.AddExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| AddExpression.change1() | 13 | 5 | 9 | 9 |
| AddExpression.change2() | 13 | 5 | 9 | 9 |
| AddExpression.derivation() | 0 | 1 | 1 | 1 |
| AddExpression.simplify() | 21 | 10 | 9 | 15 |
| AddExpression.toString() | 0 | 1 | 1 | 1 |
| Constant.Constant(BigInteger) | 0 | 1 | 1 | 1 |
| Constant.derivation() | 0 | 1 | 1 | 1 |
| Constant.getValue() | 0 | 1 | 1 | 1 |
| Constant.simplify() | 0 | 1 | 1 | 1 |
| Constant.toString() | 0 | 1 | 1 | 1 |
| CosFunction.derivation() | 0 | 1 | 1 | 1 |
| CosFunction.simplify() | 0 | 1 | 1 | 1 |
| CosFunction.toString() | 0 | 1 | 1 | 1 |
| Create.Create(String) | 0 | 1 | 1 | 1 |
| Create.expression() | 5 | 3 | 3 | 4 |
| Create.factor() | 8 | 6 | 6 | 7 |
| Create.getConstant() | 5 | 1 | 6 | 6 |
| Create.getPower() | 2 | 2 | 2 | 2 |
| Create.term() | 2 | 2 | 2 | 2 |
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| MultiplyExpression.MultiplyExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| MultiplyExpression.change1() | 3 | 3 | 3 | 3 |
| MultiplyExpression.change2() | 3 | 3 | 3 | 3 |
| MultiplyExpression.derivation() | 0 | 1 | 1 | 1 |
| MultiplyExpression.getMultiplier1() | 0 | 1 | 1 | 1 |
| MultiplyExpression.getMultiplier2() | 0 | 1 | 1 | 1 |
| MultiplyExpression.simplify() | 20 | 12 | 12 | 14 |
| MultiplyExpression.toString() | 4 | 1 | 3 | 3 |
| PowerFunction.PowerFunction(Expression,BigInteger) | 0 | 1 | 1 | 1 |
| PowerFunction.derivation() | 0 | 1 | 1 | 1 |
| PowerFunction.getPower() | 0 | 1 | 1 | 1 |
| PowerFunction.getRadix() | 0 | 1 | 1 | 1 |
| PowerFunction.simplify() | 2 | 2 | 1 | 2 |
| PowerFunction.toString() | 5 | 4 | 5 | 5 |
| SinFunction.derivation() | 0 | 1 | 1 | 1 |
| SinFunction.simplify() | 0 | 1 | 1 | 1 |
| SinFunction.toString() | 0 | 1 | 1 | 1 |
| Variant.derivation() | 0 | 1 | 1 | 1 |
| Variant.simplify() | 0 | 1 | 1 | 1 |
| Variant.toString() | 0 | 1 | 1 | 1 |
①simplify方面,由于我的数据结构选择了二叉树,并且没有在求导之后将二叉树转为多叉树进行化简,所以在二叉树化简的阶段存在了许多分支判断和子节点simplify方法的调用,所以导致了Add和Multiply中的两个simplify方法极其冗杂。
②Create类中factor()类似工厂模式,所以存在很多分支判断:常数返回Constant对象、表达式因子调用expression()的返回值等等。
自我评价
优点
此次使用了递归下降分析处理字符串和二叉树存取数据,(没有保证长度优化)具有较强的拓展性,在第三次作业只需要在读取字符串时进行类似状态机的判断和增加Sin函数和Cos函数属性就能完成了。
缺点
在长度优化方面做的不好,从这次作业中已经看出二叉树在长度优化方面比较困难,其一要进行许多的类判断(比如合并常数时要判断是否是Constant类,如果加式里其中之一是加式,又要进行对内加式的两个加式进行类型判断,极其困难),其二就是化简和换位置要进行树的遍历的操作(这一点看上去,其他人应该也得进行类似的遍历操作)。
第三次作业
类图
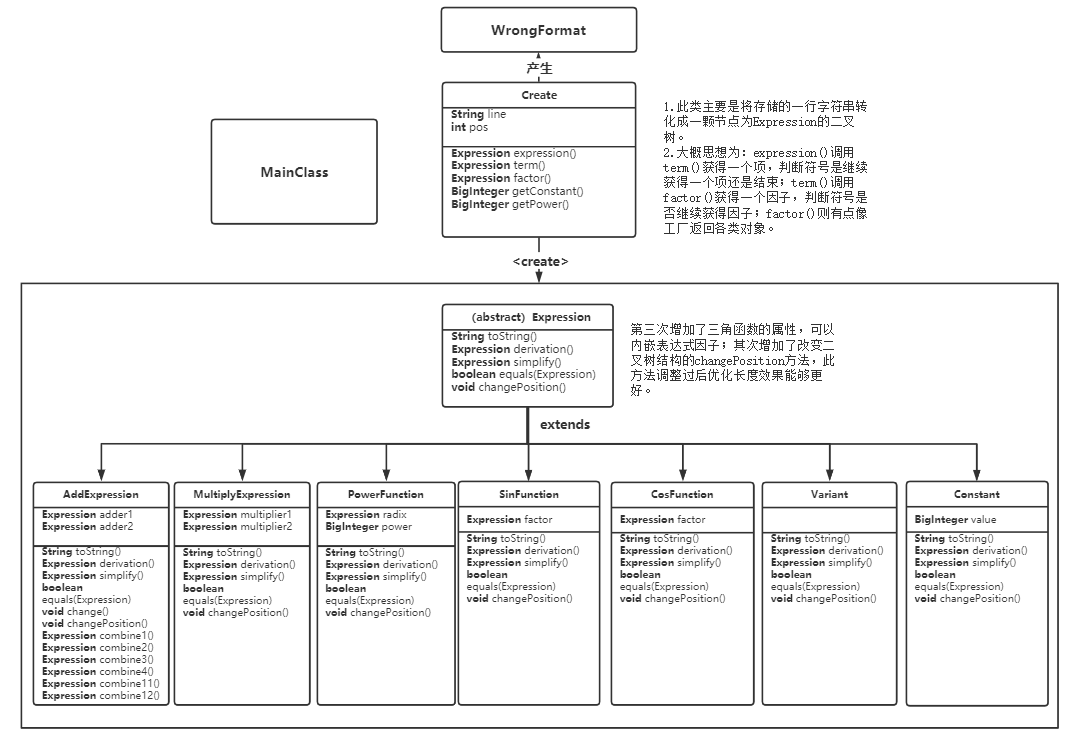
类与方法的评估
| 类/特征 | 类的规模 | 属性个数 | 方法个数 | 方法规模 | 方法分支数目 |
|---|---|---|---|---|---|
| MainClass | 19 | 0 | 1 | 15 | 无 |
| WrongFormat | 2 | 0 | 0 | 无 | 无 |
| Create | 181 | 2 | 6 | 众数20左右,最大40 | factor()较多 |
| Expression | 12 | 0 | 5 | 1 | 无 |
| AddExpression | 255 | 2 | 15 | 有5个在40左右 | 多 |
| MultiplyExpression | 143 | 130 | 8 | simplify()方法40+ | 较多 |
| PowerFunction | 63 | 53 | 7 | 众数10+ | 少 |
| SinFunction | 46 | 38 | 6 | 良好 | 少 |
| CosFunction | 48 | 40 | 6 | 良好 | 少 |
| Variant | 22 | 0 | 6 | 基本都是1行 | 无 |
| Constant | 36 | 1 | 6 | 基本都是1行 | 无 |
复杂度分析
类的复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| AddExpression | 3.6 | 12 | 54 |
| Constant | 1.14 | 2 | 8 |
| CosFunction | 1.43 | 2 | 10 |
| Create | 4.1 | 8 | 41 |
| Expression | n/a | n/a | 0 |
| MainClass | 1 | 1 | 1 |
| MultiplyExpression | 3.56 | 16 | 32 |
| PowerFunction | 1.62 | 3 | 13 |
| SinFunction | 1.43 | 2 | 10 |
| Variant | 1 | 1 | 5 |
| WrongFormat | n/a | n/a | 0 |
第三次作业的构造跟第二次作业差不多,所以AddExpression、MultiplyExpression和Create的循环度高原因跟第二次一样。
方法的复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| AddExpression.AddExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| AddExpression.change() | 0 | 1 | 1 | 1 |
| AddExpression.changePosition() | 10 | 1 | 10 | 11 |
| AddExpression.combine1() | 4 | 4 | 4 | 4 |
| AddExpression.combine11() | 14 | 7 | 15 | 15 |
| AddExpression.combine12() | 20 | 9 | 19 | 19 |
| AddExpression.combine2() | 4 | 3 | 4 | 4 |
| AddExpression.combine3() | 4 | 3 | 4 | 4 |
| AddExpression.combine4() | 2 | 2 | 4 | 4 |
| AddExpression.derivation() | 0 | 1 | 1 | 1 |
| AddExpression.equals(Expression) | 3 | 2 | 3 | 3 |
| AddExpression.getAdder1() | 0 | 1 | 1 | 1 |
| AddExpression.getAdder2() | 0 | 1 | 1 | 1 |
| AddExpression.simplify() | 19 | 12 | 13 | 18 |
| AddExpression.toString() | 0 | 1 | 1 | 1 |
| Constant.Constant(BigInteger) | 0 | 1 | 1 | 1 |
| Constant.changePosition() | 0 | 1 | 1 | 1 |
| Constant.derivation() | 0 | 1 | 1 | 1 |
| Constant.equals(Expression) | 2 | 2 | 2 | 2 |
| Constant.getValue() | 0 | 1 | 1 | 1 |
| Constant.simplify() | 0 | 1 | 1 | 1 |
| Constant.toString() | 0 | 1 | 1 | 1 |
| CosFunction.CosFunction(Expression) | 0 | 1 | 1 | 1 |
| CosFunction.changePosition() | 0 | 1 | 1 | 1 |
| CosFunction.derivation() | 0 | 1 | 1 | 1 |
| CosFunction.equals(Expression) | 2 | 2 | 2 | 2 |
| CosFunction.getFactor() | 0 | 1 | 1 | 1 |
| CosFunction.simplify() | 2 | 2 | 1 | 2 |
| CosFunction.toString() | 3 | 2 | 2 | 3 |
| Create.Create(String) | 2 | 3 | 1 | 3 |
| Create.createCosFunction() | 4 | 5 | 1 | 5 |
| Create.createSinFunction() | 4 | 5 | 1 | 5 |
| Create.eatWhitespace() | 2 | 1 | 2 | 3 |
| Create.end() | 1 | 2 | 1 | 2 |
| Create.expression() | 9 | 3 | 6 | 8 |
| Create.factor() | 7 | 6 | 8 | 8 |
| Create.getConstant() | 6 | 2 | 6 | 7 |
| Create.getPower() | 5 | 3 | 2 | 3 |
| Create.term() | 5 | 3 | 5 | 6 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| MultiplyExpression.MultiplyExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| MultiplyExpression.change() | 0 | 1 | 1 | 1 |
| MultiplyExpression.changePosition() | 10 | 1 | 10 | 11 |
| MultiplyExpression.derivation() | 0 | 1 | 1 | 1 |
| MultiplyExpression.equals(Expression) | 3 | 2 | 3 | 3 |
| MultiplyExpression.getMultiplier1() | 0 | 1 | 1 | 1 |
| MultiplyExpression.getMultiplier2() | 0 | 1 | 1 | 1 |
| MultiplyExpression.simplify() | 24 | 16 | 16 | 18 |
| MultiplyExpression.toString() | 4 | 1 | 3 | 3 |
| PowerFunction.PowerFunction(Expression,BigInteger) | 0 | 1 | 1 | 1 |
| PowerFunction.changePosition() | 0 | 1 | 1 | 1 |
| PowerFunction.derivation() | 0 | 1 | 1 | 1 |
| PowerFunction.equals(Expression) | 3 | 2 | 3 | 3 |
| PowerFunction.getPower() | 0 | 1 | 1 | 1 |
| PowerFunction.getRadix() | 0 | 1 | 1 | 1 |
| PowerFunction.simplify() | 5 | 3 | 3 | 4 |
| PowerFunction.toString() | 3 | 3 | 3 | 3 |
| SinFunction.SinFunction(Expression) | 0 | 1 | 1 | 1 |
| SinFunction.changePosition() | 0 | 1 | 1 | 1 |
| SinFunction.derivation() | 0 | 1 | 1 | 1 |
| SinFunction.equals(Expression) | 2 | 2 | 2 | 2 |
| SinFunction.getFactor() | 0 | 1 | 1 | 1 |
| SinFunction.simplify() | 2 | 2 | 1 | 2 |
| SinFunction.toString() | 3 | 2 | 2 | 3 |
| Variant.changePosition() | 0 | 1 | 1 | 1 |
| Variant.derivation() | 0 | 1 | 1 | 1 |
| Variant.equals(Expression) | 0 | 1 | 1 | 1 |
| Variant.simplify() | 0 | 1 | 1 | 1 |
| Variant.toString() | 0 | 1 | 1 | 1 |
此次作业中,我主要增加了长度优化的内容,changePosition通过局部改变二叉树的结构使得某些叶节点能够更好的结合,但是我还是继续了simplify的特判痛苦之旅,主要在度为2的节点(AddExpression和MultiplyExpression)做了许多特判情况,并且许多特判情况是重复的,例如两个叶节点我需要分别判断一次,导致有许多类似的代码。这也导致了某些方法的分支和循环都会特别多。
自我评价
优点
我觉得递归下降处理字符串和二叉树存储进行求导操作是我这份作业比较优美的地方。
缺点
像在上面所说的,可能是因为我选择了继续在二叉树内进行长度优化,各种特判进行的十分痛苦,如果可以的话,我一定会采用多叉树进行合并同类项和提取因子的。
BUG分析
我在第三次作业中被找出了一个bug。
在进行二叉树长度优化的时候,总具有两份类似的代码,我总是写了一份然后ctrl+c、ctrl+v,然后再进行修改,可是有个地方忘记修改了,导致合并同类项出现了问题。(别用二叉树优化了,痛苦ToT)
HACK策略
①测试stackoverflow的问题,因为前几次作业很多同学应该会使用正则表达式进行匹配。
②测试单一常数,虽然求导结果为0,但是有些同学的程序是没有输出结果的。
③测试求导结果比较特殊的,有时候有些同学求导结果正确,但是其输出结果的格式出了问题(出现表达式因子幂次、sin(x*x)等)。
④尝试测评机评测。
⑤第三次作业中尝试了许多可能被误判WF的样例。
重构经历总结
第一次作业要求简单,每一项都可以化简成a*x**c这种形式,所以只设计了一个Term类进行项的存储,然后再设计一个Expression类对一个表达式的所有项进行统一管理,例如求导、toString等等,因此结构较为简单(也预示着第二次作业的重构)。
第二次作业加入了三角函数和表达式因子,我第一次作业的结构不再适用(如果没有表达式因子,Term类增加两个属性应该也会适用)。一筹莫展之际,我学习了一下往年学长学姐们的blog,发现了他们是用一种递归下降分析方法来处理字符串的,然后在舍友的帮助下,成功应用了这个方法。另外,作业tips有一个将表达式转化成一棵树的建议,加上乘法求导规则的约束,我选择了二叉树结构。这种结构具有比较好的拓展性,在第三次作业只需要增加些许属性和类似状态机的判断就行了。
心得体会
经过第一单元的练习,一方面,我更加了解面向过程编程与面向对象编程的区别:面向对象更加关注各种类和类的功能;面向过程则更加注重步骤。此外的收获,初步掌握了递归下降分析,字符串处理这部分总体比较令人满意。另一方面,比较令我失望的是在长度优化上做的各种特判分支,令人痛苦(如果有下次,我会使用连乘和连加进行同类项合并和提取公因式的)。
在后续的作业中,我希望我可以做到
①从各种类和类的功能的层面关注问题 。
②学习往年学长学姐的blog,大致了解后续作业的拓展方面,便于此次作业构思。
③从实现功能的角度选择合适的数据结构。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号