堆

堆的性质

1.堆是一颗完全二叉树

2.堆的顶端一定是“最大”，最小”的，但是要注意一个点，这里的大和小并不是传统意义下的大和小，它是相对于优先级而言的，当然你也可以把优先级定为传统意义下的大小，但一定要牢记这一点，初学者容易把堆的“大小”直接定义为传统意义下的大小，某些题就不是按数字的大小为优先级来进行堆的操作的

3.堆一般有两种样子，小根堆和大根堆，分别对应第二个性质中的“堆顶最大”“堆顶最小”，对于大根堆而言，任何一个非根节点，它的优先级都小于堆顶，对于小根堆而言，任何一个非根节点，它的优先级都大于堆顶

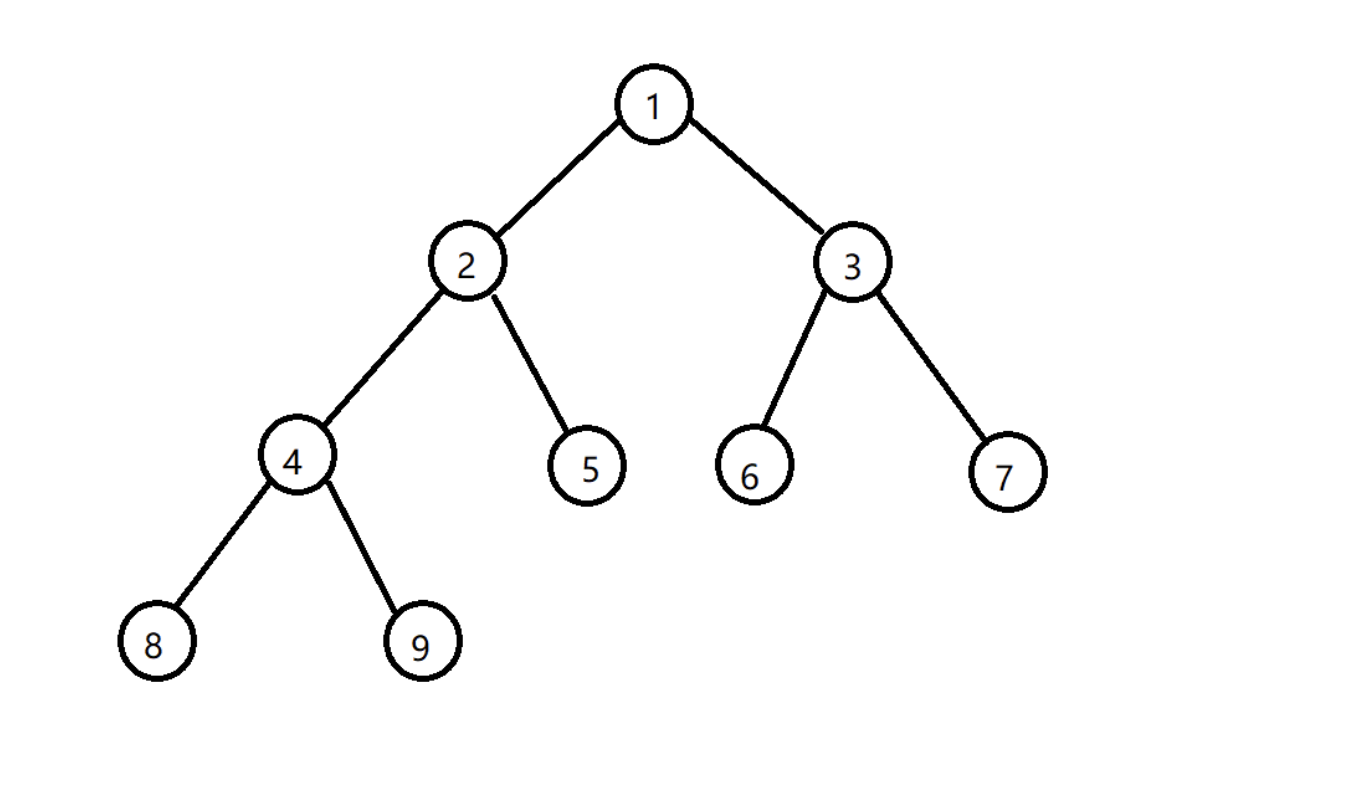
如图（小根堆） 对于堆的每个子树，它同样也是一个堆

堆的STL实现

首先你需要一个头文件：#include< queue >

priority_queue<int> q;//这是一个大根堆q
priority_queue<int,vector<int>,greater<int> >q;//这是一个小根堆q
//注意某些编译器在定义一个小根堆的时候greater<int>和后面的>要隔一个空格，不然会被编译器识别成位运算符号>>

操作

q.top()//取得堆顶元素，并不会弹出
q.pop()//弹出堆顶元素
q.push()//往堆里面插入一个元素
q.empty()//查询堆是否为空，为空则返回1否则返回0
q.size()//查询堆内元素数量

例题堆

代码展示

#include<bits/stdc++.h>
using namespace std;
int tot = 0,n;
priority_queue<int, vector<int>, greater<int> > q;
int main()
{
	cin >> n;
	for(int i = 1;i <= n; i++)
	{
	    int x;
		cin >> x;
		q.push(x);
	}
	for(int i = 1;i < n; i++)
	{
		int x = q.top();q.pop();
		int y = q.top();q.pop();
		tot += x + y;
		q.push(x + y);
	}
	cout << tot << endl;
}

. . . . . .