bzoj 3195 [Jxoi2012]奇怪的道路
3195: [Jxoi2012]奇怪的道路
Description
小宇从历史书上了解到一个古老的文明。这个文明在各个方面高度发达，交通方面也不例外。考古学家已经知道，这个文明在全盛时期有n座城市，编号为1..n。m条道路连接在这些城市之间，每条道路将两个城市连接起来，使得两地的居民可以方便地来往。一对城市之间可能存在多条道路。
据史料记载，这个文明的交通网络满足两个奇怪的特征。首先，这个文明崇拜数字K，所以对于任何一条道路，设它连接的两个城市分别为u和v，则必定满足1 <=|u - v| <= K。此外，任何一个城市都与恰好偶数条道路相连（0也被认为是偶数）。不过，由于时间过于久远，具体的交通网络我们已经无法得知了。小宇很好奇这n个城市之间究竟有多少种可能的连接方法，于是她向你求助。
方法数可能很大，你只需要输出方法数模1000000007后的结果。
Input
输入共一行，为3个整数n，m，K。
Output
输出1个整数，表示方案数模1000000007后的结果。
Sample Input
3 4 1
【输入样例2】
4 3 3
Sample Output
3
【输出样例2】
4
HINT
【数据规模】
100%的数据满足1<= n <= 30, 0 <= m <= 30, 1 <= K <= 8.
【题目说明】
两种可能的连接方法不同当且仅当存在一对城市，它们间的道路数在两种方法中不同。
在交通网络中，有可能存在两个城市无法互相到达。
可能我的大多数前辈都没有做过这道题，不然应该还是会细细深思的。网上很多题解都没有开滚动，而且开了个四维的数组，空间与时间都多了一个常数k。而POPOQQQ空间上开了三维，时间上却慢了许多。他说：“标解不是这个- - 状态多了一维，代替掉了sta2的枚举，具体做法不大清楚- - 反正比这个快了40倍- -”
我来说说我的想法吧。仨打表的，还是比我强啊。
我的空间是2*m*2^(k+1)的（2是滚动的），时间是n*(m*2^k+k*m*2^(k+1))的。在网上，我看见大多数空间与时间都多了一个常数k。也可能是我眼拙或是太没有耐心了，没有看见更快的。
而这不只是空间与时间的区别。我做过的状压题不多，但这道题的实现确实是最简单的。而有一篇博客如是说：“细节特别特别多！！！ 要看代码好好思考！！！”也有人说：“因为这道题实现起来有一些复杂，所以是一道当之无愧的好题。”
这个常数的道理在什么地方？其实想起来也很简单。借用一份题解，谢谢博主SD_le：
“
第一眼看到题比较裸的状压dp就是f[i][j][s]表示考虑到第i个点，连了j条边，i和i左边k个点奇偶性状态为s的方案数，然后枚举i和谁连边向j+1转移，每个s再向i+1转移。
写完后发现这个做法有bug，因为同一个状态因为i向外连边的顺序不同而被重复记数了。比如：
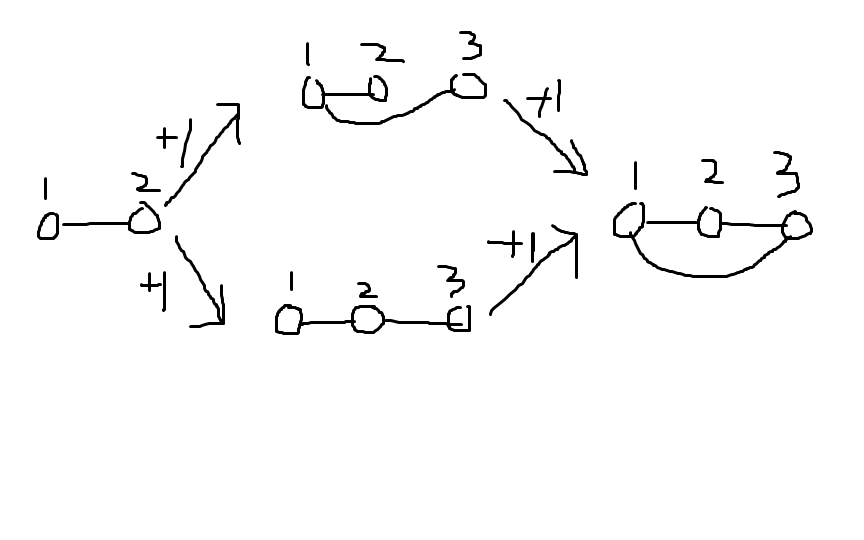
第一个状态就在第四个状态中被重复记了两次，所以我们在加一位状态l，表示i正准备和i-l连边，这样i的边就是从左往右连的，就不会重复记数了。
”
只要知道状压是什么（PS：我当然知道啊不就是状态压缩类动态规划吗），应该是很好列出来三维对应的含义的。但是，当你真正做出来时，也常常会发现上述的那个bug。有可能从一点i连到前面那几个点的边发生了重复。这就看上去很不清真了。但是，当对DP的认识上升到了沿拓扑序转移状态这样的“境界”时，你就会发现，i连向相同一个点的边就很像背包问题中的一件物品，每一件物品都是不限量的（只是最终要求了奇偶）。想一想，我们的完全背包统计方案时并没有多开一维，但绝对不会重复计数的。原因很简单，在做背包问题时，各个物品的选取存在严格顺序，不存在“选了几个物品a，又选了一点别的，再去选了几个物品a”的情况。只要能想到这里，如何解决就不是很难了。应当严格区分出各个物品，在每一个物品内部进行顺推（因为是完全背包）。
1 /************************************************************** 2 Problem: 3195 3 User: Doggu 4 Language: C++ 5 Result: Accepted 6 Time:68 ms 7 Memory:960 kb 8 ****************************************************************/ 9 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 const int M = 30 + 5; 14 const int K = 9; 15 const int MOD = 1e9+7; 16 int n, m, k, f[2][M][1<<K], cur, lm, lim, pow[K]; 17 inline void add(int &a,int b) {a=a-MOD+b>0?a-MOD+b:a+b;} 18 int main() { 19 scanf("%d%d%d",&n,&m,&k);pow[0]=1;for( int i = 1; i <= k; i++ ) pow[i]=pow[i-1]<<1; 20 f[cur][0][0]=1;lim=1<<(k+1);lm=1<<k; 21 for( int i = 1; i <= n; i++ ) { 22 cur^=1;memset(f[cur],0,sizeof(f[cur])); 23 for( int j = 0; j <= m; j++ ) for( int st = 0; st < lm; st++ ) f[cur][j][st<<1]=f[cur^1][j][st]; 24 int bound=std::min(k,i-1);for( int bit = 1; bit <= bound; bit++ ) for( int j = 0; j < m; j++ ) for( int st = 0; st < lim; st++ ) add(f[cur][j+1][st^1^pow[bit]],f[cur][j][st]); 25 } 26 printf("%d\n",f[cur][m][0]); 27 return 0; 28 }
