BZOJ 2815 [ZJOI2012]灾难

2815: [ZJOI2012]灾难

Description

　　阿米巴是小强的好朋友。 
　　阿米巴和小强在草原上捉蚂蚱。小强突然想，如果蚂蚱被他们捉灭绝了，那么吃蚂蚱的小鸟就会饿死，而捕食小鸟的猛禽也会跟着灭绝，从而引发一系列的生态灾难。 
　　学过生物的阿米巴告诉小强，草原是一个极其稳定的生态系统。如果蚂蚱灭绝了，小鸟照样可以吃别的虫子，所以一个物种的灭绝并不一定会引发重大的灾难。 
　　我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系： 
  • 一个食物网有 N个点，代表 N 种生物，如果生物 x 可以吃生物 y，那么从 y向 x 连一个有向边。
  • 这个图没有环。
  • 图中有一些点没有连出边，这些点代表的生物都是生产者，可以通过光合作用来生存； 而有连出边的点代表的都是消费者，它们必须通过吃其他生物来生存。
  • 如果某个消费者的所有食物都灭绝了，它会跟着灭绝。
  • 我们定义一个生物在食物网中的“灾难值”为，如果它突然灭绝，那么会跟着一起灭绝的生物的种数。

　　举个例子：在一个草场上，生物之间的关系是：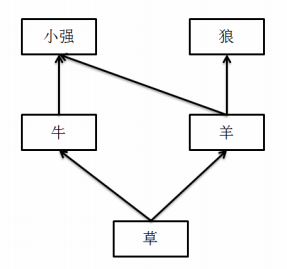 
　　如果小强和阿米巴把草原上所有的羊都给吓死了，那么狼会因为没有食物而灭绝，而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以，羊的灾难值是 1。但是，如果草突然灭绝，那么整个草原上的 5 种生物都无法幸免，所以，草的灾难值是 4。 
　　给定一个食物网，你要求出每个生物的灾难值。

Input

　　第一行是一个正整数 N，表示生物的种数。生物从 1 标号到 N。 
　　接下来 N 行，每行描述了一个生物可以吃的其他生物的列表，格式为用空格隔开的若干个数字，每个数字表示一种生物的标号，最后一个数字是 0 表示列表的结束。 

Output

 　　N行，每行一个整数，表示每个生物的灾难值。 

Sample Input

5 
0 
1 0 
1 0 
2 3 0 
2 0 

Sample Output

4 
1 
0 
0 
0 

HINT

样例输入描述了题目描述中举的例子。 

【数据规模】 
对 50%的数据，N ≤ 10000。 
对 100%的数据，1 ≤ N ≤ 65534。 
输入文件的大小不超过 1M。保证输入的食物网没有环。

　　这道题很有实际价值。

参自：http://fanhq666.blog.163.com/blog/static/8194342620124274154996/

【算法描述】
　　有这样一个事实：
　　生物之间的灭绝的结构形成了一个树，树上的一个节点的灭绝会且仅会导致以它为根的子树的灭绝。我们管这个树叫“灭绝树”。
　　对于生产者，我们给它添加一个假想的食物：太阳。
　　这样，“灭绝树”就形成了一个以太阳为根的树。
 
　　下面说明如何通过增量法把灭绝树建出来，同时也是对灭绝树的存在性的证明。
 
　　首先，把食物网按从猎物到捕食者的顺序拓扑排序。
　　之后，依次考虑每个生物i.我们已经构建好了排序在i之前的生物组成的“灭绝树”了。
　　假设i的食物有x[0]~x[k]（x[0]~x[k]在拓扑排序中比i靠前）。
　　很显然，只有x[0]~x[k]在树上的公共祖先的灭绝会导致i灭绝，否则i一定可以找到能让它活下来的食物。
　　　　　　　　　　　　．．．　　
　　　　　　　　　／　　　　　　　
　　　　　　　　／　　　　　　　　
　　　　　　ＬＣＡ　　　　　　　　
　　　　　　／｜＼　　　　　　　　
　　　　＿／　｜｜　　　　　　　　
　　　／　　　｜　＼　　　　　　　
　　Ｏ　　　　｜　　＼　　　　　　
　／　＼　　　　＼　　\　　　　　
ｘ　　　ｘ　　　　ｘ　　ｘ　　　　
　　　　　　　ｉ　　　　　　　　　
　　于是，我们可以把i挂在x[0]~x[k]的最近公共祖先下面。
　　处理完所有的生物，我们得到的树就是整个图的灭绝树了。
　　一旦得到灭绝树，每个生物的灾难值就可以通过以它为根的子树的大小减1来计算.
【复杂度分析】
　　拓扑排序的时间复杂度是O（|E|）的。
　　一共有|E|次LCA的查询，和|V|次添加边的操作。
　　我们使用某种支持快速查询LCA、添加点的数据结构（例如动态树）。
　　这样，总的时间复杂度是O(|E|log|V|)。
 
　　现在该我说了。ST表居然可以随着加边逐渐完善，实在是太强了。这真的极大的开拓了眼界，不失为一道好题。实现很简单，先建正图和反图，统计入度再拓扑排序。按拓扑序依次插入建立灭绝树（将父亲设做原图各入点在灭绝树中的LCA），最后DFS出子树siz即可。灭绝树的正确性可以使用归纳法证明，其实是很显然的。
 1 /**************************************************************
 2     Problem: 2815
 3     User: Doggu
 4     Language: C++
 5     Result: Accepted
 6     Time:216 ms
 7     Memory:17152 kb
 8 ****************************************************************/
 9  
10 #include <cstdio>
11 #include <algorithm>
12 template<class T>inline void readin(T &res) {
13     static char ch;T flag=1;
14     while((ch=getchar())<'0'||ch>'9')if(ch=='-')flag=-1;
15     res=ch-48;while((ch=getchar())>='0'&&ch<='9')res=(res<<1)+(res<<3)+ch-48;res*=flag;
16 }
17  
18 const int N = 100000;
19 const int M = 100000;
20 const int S = 20;
21 struct Edge {int v, upre;};
22 struct CON {
23     Edge e[M];int head[N], ne;
24     void adde(int u,int v) {e[++ne]=(Edge){v,head[u]};head[u]=ne;}
25 }g, vg, gg;
26  
27 int n, in[N], p[N], topo[N], stack[N], top, anc[N][S+1], dep[N], siz[N];
28 void topo_sort() {
29     int t=0;for( int i = 1; i <= n; i++ ) if(!in[i]) stack[++top]=i;
30     while(top!=0) {
31         int u=stack[top--];topo[++t]=u;
32         for( int i=g.head[u]; i; i=g.e[i].upre ) {
33             int v=g.e[i].v;
34             in[v]--;if(!in[v]) stack[++top]=v;
35         }
36     }
37 }
38 int LCA(int u,int v) {
39     if(dep[u]<dep[v]) std::swap(u,v);
40     for( int t=dep[u]-dep[v], p=0; t; t>>=1, p++ ) if(t&1) u=anc[u][p];
41     if(u==v) return u;
42     for( int p=S; p>=0&&anc[u][0]!=anc[v][0]; p-- ) if(anc[u][p]!=anc[v][p]) u=anc[u][p], v=anc[v][p];
43     return anc[u][0]; 
44 }
45 void DFS(int u,int fa) {
46     siz[u]=1;
47     for( int i=gg.head[u]; i; i=gg.e[i].upre ) {
48         int v=gg.e[i].v;
49         if(v==fa) continue;
50         DFS(v,u);
51         siz[u]+=siz[v];
52     }
53 }
54 int main() {
55     readin(n);
56     for( int v = 1,u; v <= n; v++ ) while(1) {
57         readin(u);if(u==0) break;
58         g.adde(u,v);
59         vg.adde(v,u);
60         in[v]++;p[v]++;
61     }
62     for( int v = 1; v <= n; v++ ) if(!in[v]) g.adde(n+1,v), vg.adde(v,n+1), in[v]++, p[v]++;
63     n++;topo_sort();
64     for( int i = 1; i <= n; i++ ) {
65         anc[i][0]=i;
66         dep[i]=1;
67     }
68     for( int i = 1; i <= n; i++ ) {
69         int u=topo[i];
70         if(!p[u]) continue;bool first=1;int ca;
71         for( int i=vg.head[u]; i; i=vg.e[i].upre ) {
72             int v=vg.e[i].v;
73             if(first) ca=v, first=0;
74             else ca=LCA(ca,v);
75         }
76         gg.adde(ca,u);
77         anc[u][0]=ca;
78         for( int i = 1; i <= S; i++ ) anc[u][i]=anc[anc[u][i-1]][i-1];
79         dep[u]=dep[ca]+1;
80     }
81     DFS(n,n);
82     for( int i = 1; i < n; i++ ) printf("%d\n",siz[i]-1);
83     return 0;
84 }
85
灭绝树
posted @ 2017-07-06 11:52  Doggu  阅读(182)  评论(0)  编辑  收藏  举报