NOIP 2016-day1
pts: 200
T1: 100
T2: 0
T3: 100
T1
[NOIP2016 提高组] 玩具谜题
模拟
solution
无脑 模拟
/*
work by:Ariel_
*/
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
int read(){
int x = 0,f = 1; char c = getchar();
while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
return x*f;
}
int n, m, now;
struct node{int fx; string name;}a[N];
int main(){
//freopen("toy.in", "r", stdin);
//freopen("toy.out", "w", stdout);
n = read(), m = read();
for (int i = 0; i < n; i++) a[i].fx = read(), cin>>a[i].name;
for (int i = 1; i <= m; i++) {
int f = read(), tep = read();
if ((!f && !a[now].fx) || (f && a[now].fx)) now = (now + n - tep) % n;
else now = (now + tep) % n;
}
cout<<a[now].name;
puts("");
return 0;
}
T2
[NOIP2016 提高组] 天天爱跑步
LCA,开桶,容斥,推柿子
吐槽:考场上硬肝一个小时,发现数据点好水,以为能水 80 分,结果直到交卷才发现读错题了 /jk
solution
据说是 noip 史上最难的神题 QWQ
这个题主要是用了桶的思想(第一次做树上开桶,容斥的题)
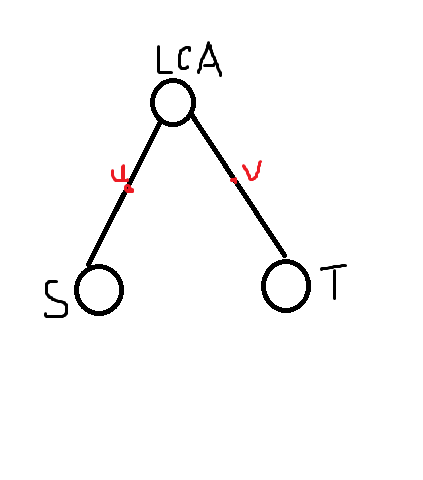
显然,对于路径 \(S-T\) 上行路段的 \(u\) 结点,如果它想要观察这个人,那么显然 \(dep[u] + w[u] = dep[s]\)
同理对于下行路段 \(v\),必须满足 \(dep[s] - dep[lca] + dep[v] - dep[lca] = w[v]\)
化简得到:\(w[v] - dep[v] = dist[s, t] - dep[t]\)
对于每个节点存在两个值 \(dep[u] + w[u], w[u] - dep[u]\)
对于每一条路径存在两个值,\(dep[s],dist[s, t] - dep[t]\) 想让它们两两匹配,开桶就好了
当遍历到 \(u\) 结点的时候,判断它可以观察到多少个人,首先把桶内之前的值存下来 \(t1, t2\) 在这个子树中显然不能产生贡献,所以最后的答案要减去
回溯的时候更新桶和答案,用邻接链表记录下以每个节点作为起点、终点和LCA的路径的标号,方便按照上式快速更新桶中的内容。记录下新的答案
在最后,以 \(u\) 为 \(LCA\) 的路径就不能对它上面的节点做出贡献了,所以要把多余贡献减去。
最后还要注意,如果一条路径的 \(LCA\) 节点可以观察到它本身,意味着这个点计算了两次贡献,一次上行一次下行,需要减去一次
/*
work by:Ariel_
*/
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 300000;
int read(){
int x = 0,f = 1; char c = getchar();
while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
return x*f;
}
int n, m;
struct edge{int v, nxt;}e[N << 1], e1[N << 1], e2[N << 1];
int head[N], E;
void add_edge (int u, int v) {//存图
e[++E] = (edge){v, head[u]};
head[u] = E;
}
int E1, E2, head1[N], head2[N];
void add1 (int v, int id) {//以 v 为终点的所有路径的集合
e1[++E1] = (edge){id, head1[v]};
head1[v] = E1;
}
void add2 (int v, int id) { //以 v 为 lca 的所有路径的集合
e2[++E2] = (edge) {id, head2[v]};
head2[v] = E2;
}
int siz[N], fa[N], dep[N], top[N], son[N];
namespace LCA{
void dfs (int x, int f){
siz[x] = 1, dep[x] = dep[f] + 1, fa[x] = f;
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if(v == f) continue;
dfs(v, x);
siz[x] += siz[v];
if(siz[son[x]] < siz[v]) son[x] = v;
}
}
void dfs2 (int x, int tp) {
top[x] = tp;
if(son[x]) dfs2(son[x], tp);
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if (v == fa[x] || v == son[x]) continue;
dfs2(v, v);
}
}
int get_lca (int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
return x;
}
}
using namespace LCA;
int b1[N << 1], b2[N << 1];//两个桶
int cnt[N], dist[N], s[N], t[N], ans[N], w[N];
void work(int x) {
int t1 = b1[w[x] + dep[x]], t2 = b2[w[x] - dep[x] + N];///遍历该点之前原先桶内的值
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if (v == fa[x]) continue;
work(v);
}
b1[dep[x]] += cnt[x];//计算上行路径该点作为起点
for (int i = head1[x]; i; i = e1[i].nxt) {//下行路径中,该点作为终点
int v = e1[i].v;
b2[dist[v] - dep[t[v]] + N]++;
}
ans[x] += b1[dep[x] + w[x]] - t1 + b2[w[x] - dep[x] + N] - t2;
for (int i = head2[x]; i; i = e2[i].nxt) {//减去以此结点为lca的终点和起点的贡献
int v = e2[i].v;
b1[dep[s[v]]]--;
b2[dist[v] - dep[t[v]] + N]--;
}
}
int main(){
n = read(), m = read();
for (int i = 1, u, v; i < n; i++) {
u = read(), v = read();
add_edge(u, v), add_edge(v, u);
}
dfs(1, 0), dfs2(1, 1);
for (int i = 1; i <= n; i++) w[i] = read();
for (int i = 1; i <= m; i++) {
s[i] = read(), t[i] = read();
int lca = get_lca(s[i], t[i]);
dist[i] = dep[s[i]] + dep[t[i]] - 2 * dep[lca];
cnt[s[i]]++;
add1(t[i], i), add2(lca, i);
if (dep[lca] + w[lca] == dep[s[i]]) ans[lca]--;
}
work(1);
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
puts("");
return 0;
}
T3
[NOIP2016 提高组] 换教室
dp,期望
solution
\(f[i][j][1/0]\) 表示当前在 \(i\) 时间点,申请了 \(j\) 次,这次申不申请的的最短路径
转移枚举这次申不申请和上次申不申请就好了
转移式子看代码 (太长,懒得写了 = =)
/*
work by:Ariel_
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 2000 + 5;
const double inf = 1e17 + 5;
int read(){
int x = 0,f = 1; char c = getchar();
while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
return x*f;
}
int n, m, v, e, c[N], d[N], dis[N][N];
double k[N], f[N][N][2], ans = 0x3f3f3f3f3f;
namespace Ariel_{
void pre() {
for (int k = 1; k <= v; k++)
for (int i = 1; i <= v; i++)
for (int j = 1; j <= v; j++) dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
for (int i = 1; i <= v; i++) dis[i][i] = 0;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) f[i][j][0] = f[i][j][1] = inf;
f[1][0][0] = f[1][1][1] = 0;
}
void work() {
for (int i = 2; i <= n; i++) {
f[i][0][0] = f[i - 1][0][0] + dis[c[i - 1]][c[i]];
for (int j = 1; j <= m; j++) {
f[i][j][0] = min(f[i][j][0], min(f[i - 1][j][0] + dis[c[i - 1]][c[i]], f[i - 1][j][1] + k[i - 1] * dis[d[i - 1]][c[i]] + (1 - k[i - 1]) * dis[c[i - 1]][c[i]]));
f[i][j][1] = min(f[i][j][1], min(f[i - 1][j - 1][0] + k[i] * dis[c[i - 1]][d[i]] + (1 - k[i]) * dis[c[i - 1]][c[i]], f[i - 1][j - 1][1] + k[i] * k[i - 1] * dis[d[i - 1]][d[i]] + (1 - k[i]) * k[i - 1] * dis[d[i - 1]][c[i]] + k[i] * (1 - k[i - 1]) * dis[c[i - 1]][d[i]] + dis[c[i - 1]][c[i]] * (1 - k[i]) * (1 - k[i - 1])));
}
}
}
void main() {
n = read(), m = read(), v = read(), e = read();
for (int i = 1; i <= n; i++) c[i] = read();
for (int i = 1; i <= n; i++) d[i] = read();
for (int i = 1; i <= n; i++) scanf("%lf", &k[i]);
memset(dis, 0x3f, sizeof dis);
for (int i = 1, u, v, w; i <= e; i++) {
u = read(), v = read(), w = read();
dis[u][v] = dis[v][u] = min(dis[u][v], w);
}
pre(), work();
for(int j = 0; j <= m; j++) ans = min(ans, min(f[n][j][0], f[n][j][1]));
printf("%.2f", ans);
}
}
int main(){
//freopen("classroom.in", "r", stdin);
//freopen("classroom.out", "w", stdout);
Ariel_::main();
puts("");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号