Loading

插头dp

PlugDP

目录

在此衷心感谢 interestingLSY 提供思路和图

从入门到吐血再到跳楼的一下午

简介：

插头 \(dp\) ，基于联通性的状压 \(dp\) ，本质还是状压 \(dp\) ；

常见的联通问题：多回路问题、路径问题、简单回路问题、广义路径问题、生成树问题

板子

一个 \(m * n\) 的棋盘，有的格子是障碍，问共有多少条回路使得经过每个非障碍格子恰好一次

\(m, n ≤ 12\)

solution

几个概念（important）：

  • 啥是插头？

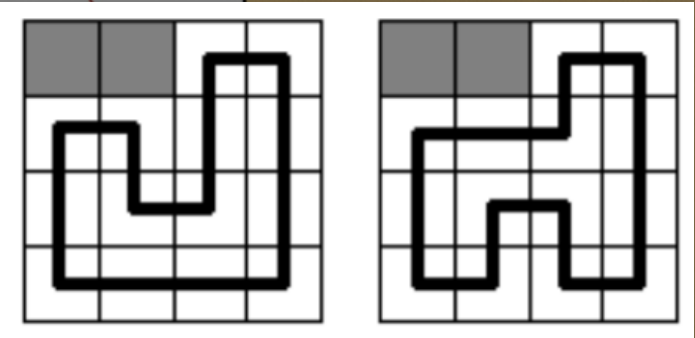
​ 一个格子通过某些方向与另一个格子相连，这些连接的位置叫做“插头”。形象地理解，网格图上每一个格子是一块拼图，那么两块拼图的接口就叫做“插头”

一个回路中，一个格子的插头最多有两个，一个进来，一个出去

图中的箭头部分就是插头

  • 轮廓线

插头 \(dp\) 不像其他的状压 \(dp\) 逐行转移，而是逐格转移的，所以我们画一条线，把已经 \(dp\) 完的格子和没有 \(dp\) 的格子分隔开，这条线就是轮廓线

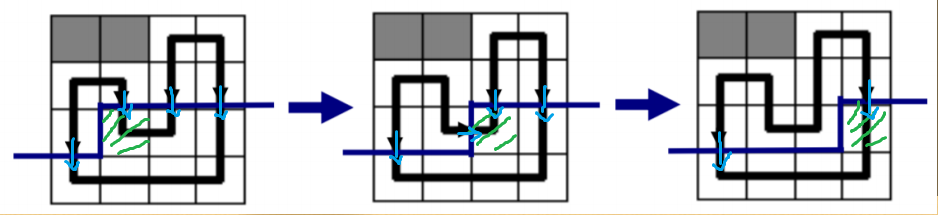
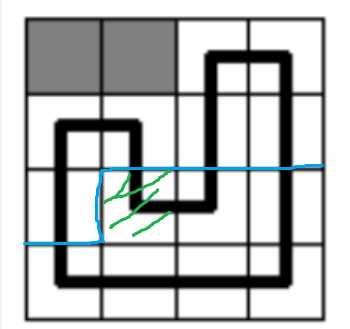
如图，绿色的是正在考虑的格子，蓝色的是插头，折线就是轮廓线

第一个图中有四个下插头，第二个图中有一个右插头和三个下插头，第三个图中有两个下插头

  • 插头之间的连通性

如果两个插头在 \(dp\) 完的部分联通，那么我们就称这两个插头互相联通

状态

\(f[i][j][S]\) 为转移到 \((i, j)\) 这个格子，轮廓线上插头的状态为 \(S\) 时的方案数

状态 \(S\) 怎么表示呢？

  • 最小表示法

我们对联通块由左向右依次标号，一个位置要么有插头，要么没有插头，所以我们可以在没有插头的地方放一个 \(0\) 有插头的地方表示为所联通的插头的编号 (所在的联通块的编号)

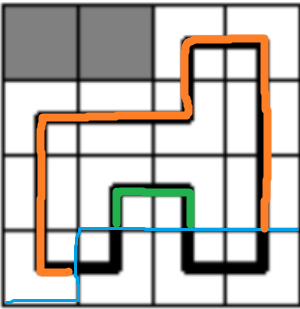
图中对应的 \(S\) 为 01221

这样我们转移就有了三种方法：

  • 新建插头
  • 连接两个插头
  • 保持原来的插头

很显然，前两种情况都需要重新对联通块标号，重新表示

对应的三种情况如下图

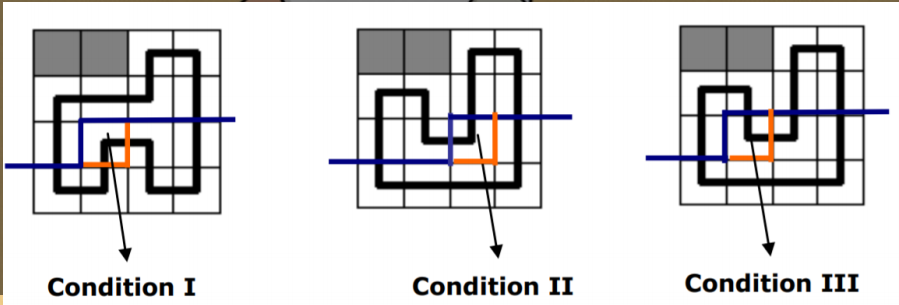
这样就可以进行转移了

  • 括号表示法

  1. 不难发现只要插头出现一定是偶数个，并且两两配对

    一个插头不可能只有头，没有尾，进去了当然要出来

  2. 插头不肯能是交叉匹配的

    从左到右有4个插头 \(a,b,c,d\)，那么绝对不能出现 \(a,c\) 匹配 \(b,d\) 匹配

    因为如果 \(a, c\) 匹配，\(b ，c\) 匹配，那么轮廓线上方就会出现交叉，就不符合题意了

根据这个不难想到括号序列 不可能交叉匹配

我们把当前正在考虑的格子左边的插头看做左括号，格子右边的插头看做右括号

那这个图的状态就可以表示为 (#()) # 表示没有括号

这样我们就可以用一个括号序列表示 \(S\)

这个括号序列可以用一个四进制来存（相比三进制方便运算）

转移

分类讨论，建议慢点开车（雾）@@

Case 1

当前考虑的格子上没有左插头和上插头但有下插头和上插头，会新建一个联通块

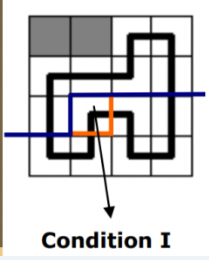
对应的括号序列由 (###) -> (()#)

Case 2

当前考虑的格子上有上插头和左插头，相当于合并两个(或一个)联通分量

下图是左插头为 "(" ，上插头为 ")" 的情况

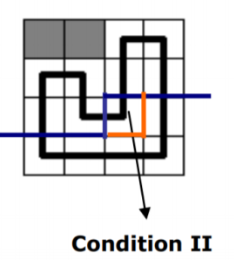
对应的括号序列由 (#()) ->(###)

Case 3

左插头或者上插头有一个，延续原来的状态

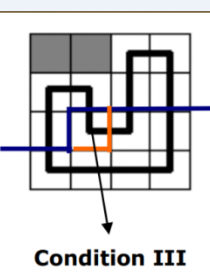
原来括号序列为 (#()#) -> (#()#)

然后，就

\(finish\) 了

posted @ 2021-05-08 17:32  Dita  阅读(293)  评论(3)    收藏  举报