网络流
网络流
from: Pecco
概念
-
范围: 有向图
-
源点: 出度为 0 的点
-
汇点: 入度为 0 的点
-
中间点: 除了汇点和源点其他的点
-
容量和流量: 每条有向边上有流量 \(c[i,j]\) 和容量 \(f[i,j]\);
有关容量和流量:
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然,流量 \(\leq\) 容量,对于中间点,所有流入的量等于流出的量
最大流
求从源点最大能流出多少,且不超过每条边的容量
souliton
可行流: 所有边上的容量都没有超过容量
栗子:零流(所有流量都为0)
从零流考虑,假设有一条路,可以从源点一直连到了汇点,并且路上的每一段流量都 < 容量,我们考虑这条路径的每一条边,找出边的容量和流量相差最小的一个来 \((delta)\) ,然后把所有的边的流量都加上这个 \(delta\),可以保证仍然是个可行流。
这样就得到了一个更大的流(原来流量+\(delta\)),这条路叫做增广路;我们不断的增大流量,直到当找不到增广路的时候,这个流就是最大流
当增加流量的时候通常用把这条路上所有的容量-delta
Ford-Fulkerson算法(FF)
核心:找增广路
\(dfs\) 不断找增广路,直到找不到为止???
栗子
边上数字代表容量
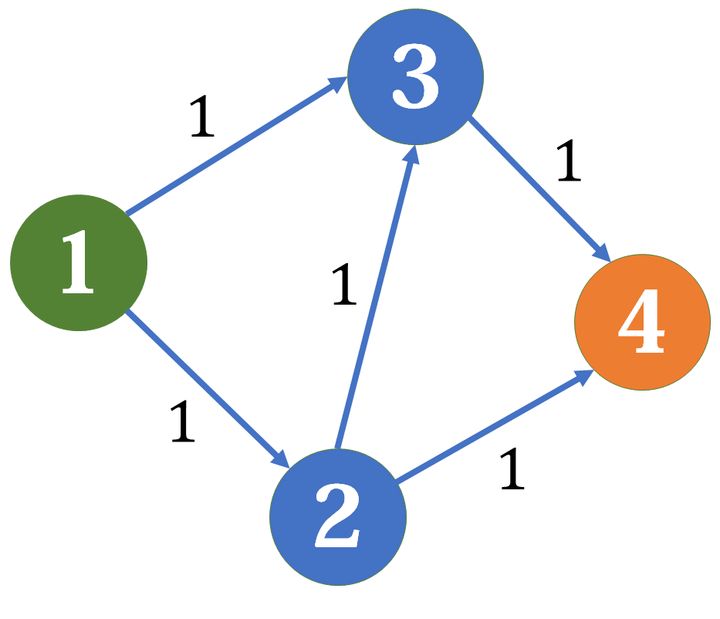
首先找到了 \(1->2->3->4\) 这条边,那么残余网格会变成这样:

现在已经找不到任何增广路了,最终求得最大流是 \(1\),但是,很明显,如果我们分别走 \(1->3->4\) 和 \(1->2->4\),可以得到 \(2\) 的最大流的
solution
反向边我们建边的时候,顺便建一条反向边
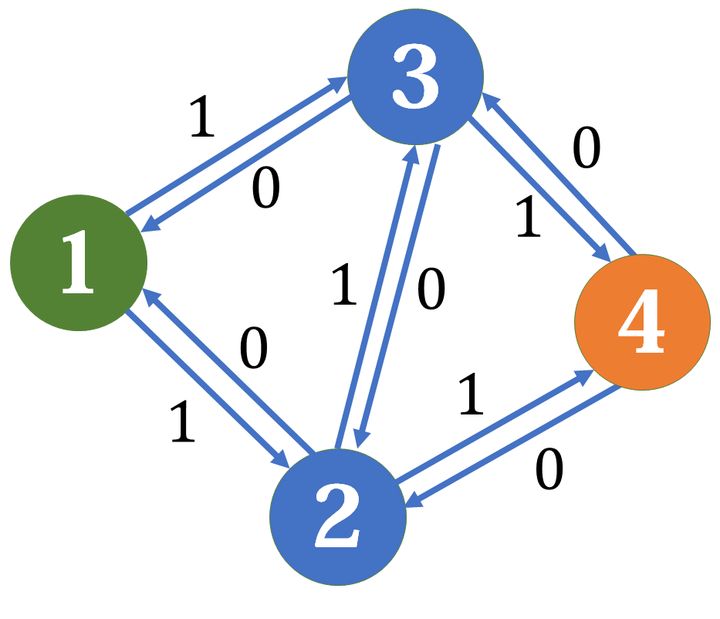
我们仍然选择 \(1->2->3->4\),但在扣除正向边的容量时,反向边要加上等量的容量
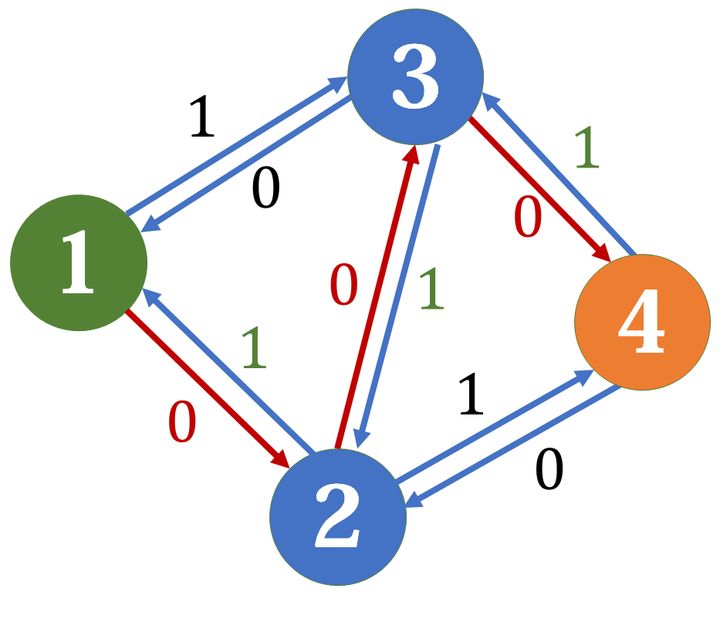
这时我们可以另外找到一条增广路:\(1->3->2->4\)
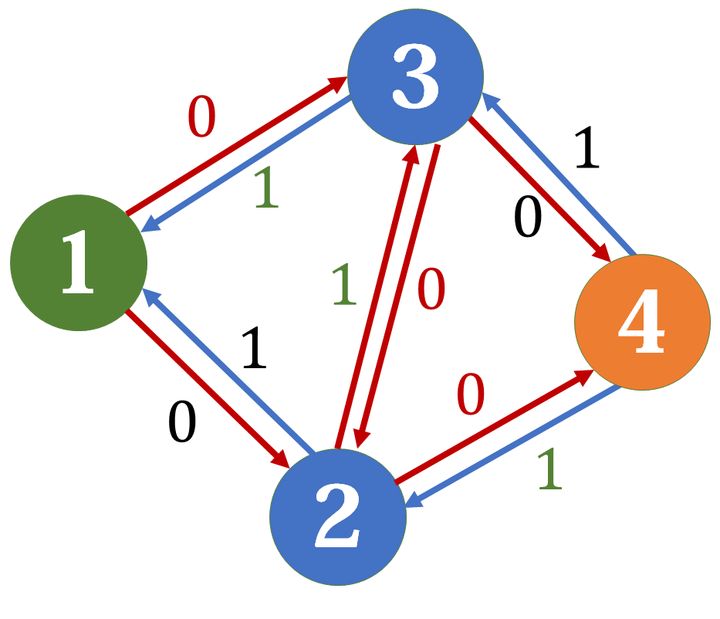
在我们同时选择了 \(2->3\) 和 \(3->2\) 两条边,我们可以认为,这两条边上的水流抵消了。所以实际上选择的路径就是 \(1->3->4\) 和 \(1->2->4\)
我们可以把反边可以理解为撤销操作
加入了反向边这种反悔机制后,我们就可以保证,当找不到增广路的时候,流到汇点的流量就是最大流
链表取反边??
\(e[i \bigoplus 1].w\) 就是 \(e[i].w\) 的反边
时间复杂度:
上界: \(O(ef)\) \(e\) 为边数,\(f\) 为最大流
code
int n, m, s, t;// s是源点,t是汇点
bool vis[M];
int dfs(int p = s, int flow = INF){
if (p == t)
return flow; // 到达终点,返回这条增广路的流量
vis[p] = true;
for (int i = head[p]; i; i = e[i].nxt){
int v = e[i].v, w = e[i].w, c;
// 返回的条件是残余容量大于0、未访问过该点且接下来可以达到终点(递归地实现)
// 传递下去的流量是边的容量与当前流量中的较小值
if (w > 0 && !vis[v] && (c = dfs(v, min(w, flow))) != -1){
e[i].w -= c;
e[i ^ 1].w += c;// 取反向边的一种简易的方法
// 建图时要把cnt置为1,且要保证反向边紧接着正向边建立
return c;
}
}
return -1; // 无法到达终点
}
int FF(){
int ans = 0, c;
while ((c = dfs()) != -1){
memset(vis, 0, sizeof(vis));
ans += c;
}
return ans;
}
Edmond-Karp算法(EK)
\(bfs\) 实现的 FF 算法
需要新开一个数组,记录每个点的前驱 \(next\),以便搜到汇点的时候原路返回,同时把反边加上容量(顺便可以根据这个判断有个点有没有被搜过)
inline int bfs(){
memset(last, -1, sizeof(last));
queue<int> q;
q.push(s);
flow[s] = 0x3f3f3f3f;
while (!q.empty()){
int p = q.front();
q.pop();
if (p == t) // 到达汇点,结束搜索
break;
for (int i = head[p]; i; i = e[i].nxt){
int v = e[i].v, w = e[i].w;
if (w > 0 && last[v] == -1){ // 如果残余容量大于0且未访问过(所以last保持在-1)
last[v] = i;
flow[v] = min(flow[p], w);
q.push(v);
}
}
}
return last[t] != -1;
}
int EK(){
int maxflow = 0;
while (bfs()){
maxflow += flow[t];
for (int i = t; i != s; i = e[last[i] ^ 1].v){ // 从汇点原路返回更新残余容量
e[last[i]].w -= flow[t];
e[last[i] ^ 1].w += flow[t];
}
}
return maxflow;
}
Dinic算法
\(FF/EK\) 算法滴优化
上面两个算法都是不断从源点找增广路,而 \(Dinic\) 只需要从源点一次 \(DFS\) 就可以实现多次增广
它选择用 \(BFS\) 分层用 \(DFS\) 查找
时间复杂度:\(O(v^2e)\)
分层:预处理出从源点到每个点的距离(不是权值,是边数)(每次循环都要预处理一次,因为有些边容量为0,可能不能走)
\(dfs\) ,从层数小的向层数大的 \(dfs\)
举个栗子 ——by:_rqy
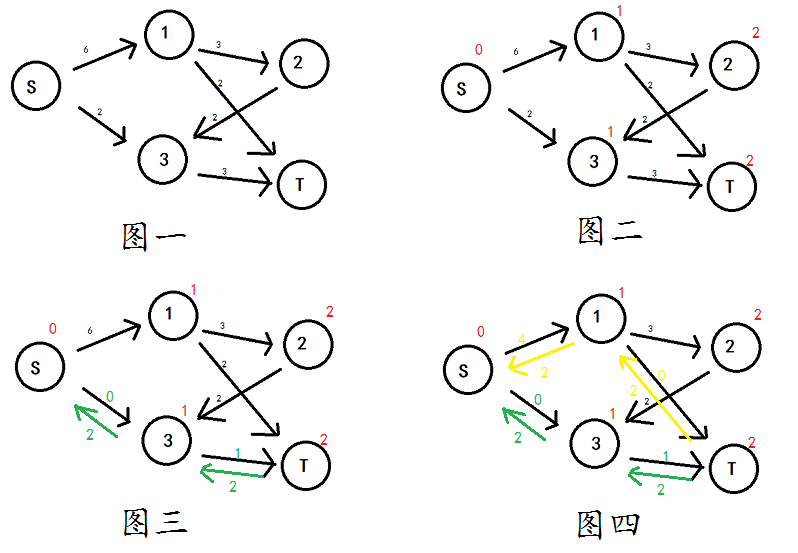
有个图一
\(BFS\) 分完层以后,对每个点标号,如图二
选 \(S-3-T\) 这条路径增广,如图三
发现 \(S-1-T\) 这条路径路径也能增广,如图四
然后。。
再也没有长度为 \(2\) 的最短路了,一轮的增广就结束了
考虑 \(dfs\)
在某个点 \(dfs\) 找到一条增广路之后,如果还剩流量没有用,就继续从这个点 \(dfs\) 找更多增广路
当前弧优化
经过一轮的增广之后,被增广的边就不会再被增广了,所以下一次就不需要考虑这条边(可以根据上面的图理解),把 \(head\) 复制一份(就可以跳过以前访问的边), 不断更新增广的起点
code
int n, m, s, t, lv[N], cur[N];//lv是每个点层数,cur用于当前弧优化增广起点
bool bfs(){// BFS分层
memset(lv, -1, sizeof(lv));
lv[s] = 0;
memcpy(cur, head, sizeof(head));// 当前弧优化初始化
queue <int> q;
q.push(s);
while(!q.empty()){
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt){
int v = e[i].v,w = e[i].w;
if (w > 0 && lv[v] == -1)
lv[v] = lv[u] + 1,q.push(v);
}
}
return lv[t] != -1; // 如果汇点未访问过说明已经无法达到汇点,此时返回false
}
int dfs(int u = s, int flow = 0x3f3f3f3){
if(u == t) return flow;
int res = flow;//剩余的流量
for (int i = cur[u]; i && res; i = e[i].nxt){// 如果已经没有剩余流量则退出
cur[u] = i;//当前弧优化
int v = e[i].v,w = e[i].w;
if (w > 0 && lv[v] == lv[u] + 1){// 往层数高的方向增广
int c = dfs(v, min(w, res));
res -= c;
e[i].w -= c;
e[i ^ 1].w += c;
}
}
return flow - res;
}
int dinic(){
int ans = 0;
while(bfs())
ans += dfs();
return ans;
}
关于时间复杂度
FF:

EK

dinic



 浙公网安备 33010602011771号
浙公网安备 33010602011771号