KMP

KMP算法

特别感谢 orz sofu6 让我悟了

\(KMP\) 算法指的是字符串模式匹配算法,要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题

说简单点就是我们平时常说的关键字搜索。模式串就是关键字（接下来称它为P），如果它在一个主串（接下来称为T）中出现，就返回它的具体位置，否则返回-1（常用手段）。

暴力算法

从左到右一个个匹配，如果这个过程中有某个字符不匹配，就跳回去，将模式串向右移动一位

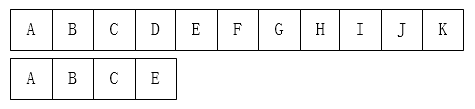
我们可以这样初始化：

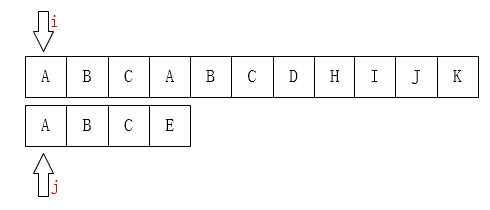
之后我们只需要比较 \(i\) 指针指向的字符和 \(j\) 指针指向的字符是否一致。如果一致就都向后移动，如果不一致

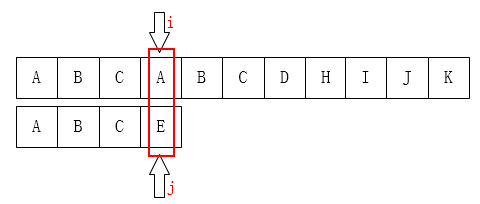
\(A\)和\(E\)不相等，那就把 \(i\) 指针移回第 \(1\) 位（假设下标从 \(0\) 开始），j移动到模式串的第\(0\)位，然后又重新开始这个步骤：

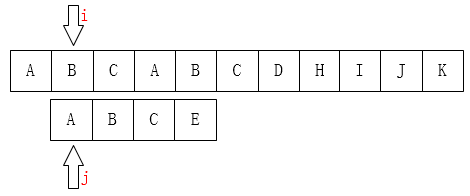
显然肯定会T掉，怎么优化？？

KMP算法

利用已经部分匹配这个有效信息，保持 \(i\) 指针不回溯，通过修改 \(j\) 指针，让模式串尽量地移动到有效的位置

那么当发现一个字符与主串不匹配时，\(j\) 指针应该移向哪儿？？

探究 \(j\) 移动的规律

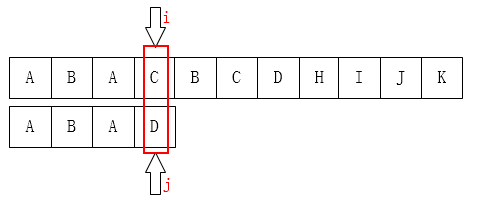
C 和 D 不匹配了把 \(j\) 移动到哪儿？？显然是第一位

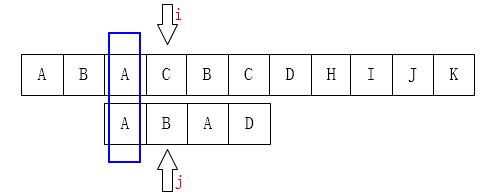
下面情况相同

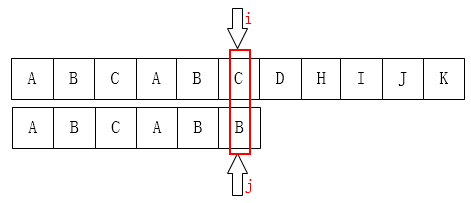
可以把 \(j\) 移到第2位，因为前面有两个字母已经匹配

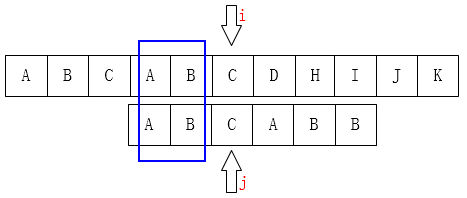
得出KMP精髓

\(j\) 要移动的下一个位置 \(k\) 要保证最前面 \(k\) 个字符 \(j\) 之前的最后 \(k\) 个字符是一样的

\(P[0 => k-1] == P[j-k => j-1]\)

另一种理解

若子串的前缀集和后缀集中，重复的最长子串的长度为\(k\)，则下次匹配子串的j可以移动到第 \(k\) 位(下标为0为第0位)

在“aba”中，前缀集就是除掉最后一个字符'a'后的子串集合{a,ab}，同理后缀集为除掉最前一个字符a后的子串集合{a,ba}，那么两者最长的重复子串就是a，k=1；

在“ababa”中，前缀集是{a,ab,aba,abab}，后缀集是{a,ba,aba,baba}，二者最长重复子串是aba，k=3；

图解

发现 \(C\) 和 \(D\) 不匹配 \(j\) 位前面的子串是 \(ABA\) ，该子串的前缀集是\({A,AB}\)，后缀集是\({A,BA}\)，最大的重复子串是\(A\)，只有\(1\)个字符，所以j移到 \(k\) 即第1位

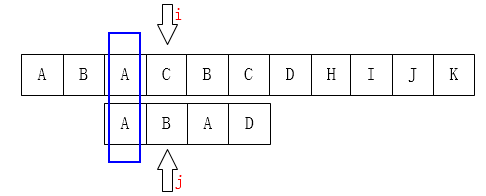
同理

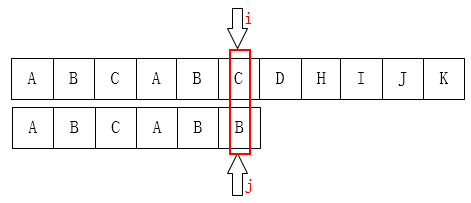
在 \(j\) 位的时候，\(j\)前面的子串是\(ABCAB\)，前缀集是\({A,AB,ABC,ABCA}，\)后缀集是\({B,AB,CAB,BCAB}\)，最大重复子串是 \(AB\)，个数是\(2\)个字符，因此\(j\) 移到 \(k\) 即第2位。

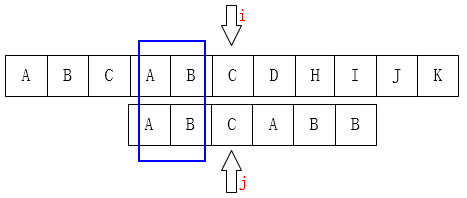
匹配时的代码

void pre(){
	for(int i = 2,j = 0;i <= m; i++){
		while(j > 0 && b[i] != b[j + 1])j = P[j];//匹配失败，退步
		if(b[i] == b[j + 1]) j++;//匹配成功，继续匹配
		P[i] = j;
	}
} 

important

怎么求这些 \(k\) 呢？？

因为在 \(P\) 的每一个位置都可能发生不匹配，所以我们要计算每一个位置 \(j\) 对应的 \(k\) ,用一个\(P\)数组保存（B[j] = k）当 A(主串)[i] != B[ j ]时，\(j\) 指针的下一个位置，因为下标从0开始的，\(k\) 值实际是 \(j\) 位前的子串的最大重复子串的长度

\(P[j]\) 的值（也就是\(k\)）表示，当\(B[j] != A[i]\)时，\(j\) 指针的下一步移动位置。

我们用递推的思想

对\(B = “ababacb”\)预处理，我们假设已经求出了\(P[1],P[2],P[3],P[4],\)求\(P[5],P[6]\)

    1 2 3 4 5 6 7
B = a b a b a c b
P = 0 0 1 2 ? ? ?  

很显然$ P[5] = P[4] + 1\(,因为\)P[4]\(可以知道\)B[1……2]\(已经和\)B[3……4]$相等了，现在又有 \(B[3] = B[5]\),所以\(P[5]\)可以用\(P[4]\)加一个字符得到所以如果在匹配过程中在\(P[5]\)位置不同的时候，直接把\(j\)移到4（P[5] + 1）的位置进行比较

而接着看\(P[6]\) ,它显然不是\(P[5] + 1\),因为\(P[P[5] + 1] != B[6]\)那么就要考虑“退一步”，将\(j\)退到\(P[P[3] + 1]\)与A[i]比较，还不匹配，再退发现为\(P[1] = 0\),stop

注意

看清查找子串时，在主串中能不能交叉，举个例子：A = 'aaaaaa',B = 'aa',如果不能交叉，匹配完成就直接返回 \(j = 0\) ,如果允许在主串中重复时，如果返回 \(j = 0\) ，就会漏掉连续的\(2,3|4,5\)位置的子串aa;所以应该返回 \(j = P[j]\) ;

int ans = 0,j = 0;
for(int i = 1;i <= n; i++){
     while(j > 0 && a[i] != b[j + 1])j = P[j];
	if(a[i] == b[j + 1])j++;
	     if(j == m){
		ans++,j = 0;
	  }
    }
return ans;

模板体

/*
  work by:Ariel
*/
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int A = 1e3 + 2;
int P[A], n, m;
char a[A], b[A];
void pre(){
	P[1] = 0;
	int j = 0;
	for(int i = 1;i < m; i++){
		while(j > 0 && b[i + 1] != b[j + 1])j = P[j];
		if(b[i + 1] == b[j + 1]) j++;
		P[i + 1] = j;
	}
} 
int kmp(){
	int ans = 0,j = 0;
	for(int i = 0;i < n; i++){
		while(j > 0 && a[i + 1] != b[j + 1])j = P[j];
		if(a[i + 1] == b[j + 1])j++;
		if(j == m){
			ans++; j = 0;
		}
	}
	return ans;
}
int main(){
  while(cin >> a + 1){
  	if (a[1] == '#')break;
  	scanf("%s",b + 1);
  	m = strlen(b + 1);
  	n = strlen(a + 1);
  	pre();
  	printf("%d\n",kmp());
  }
  
}

Power Strings

hash可以水？？

solution:

\(KMP\)一个简单的应用，要求主串中最多子串的个数，联想 \(KMP\) 自我匹配函数

不难发现如果\(n % (n - p[n]) == 0\)那就证明有子串，子串长度为\(n - p[n]\),所以最多子串个数为\(n / (n - p[n])\)

然后就套模板了

/*
  work by:Ariel
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
const int A = 1e6 + 5;
const int inf = 0x3f3f3f3f;
int p[A],n;
char a[A];
void pre(){
	p[1] = 0;
	for(int i = 1,j = 0;i < n; i++){
		while(j > 0 && a[i + 1] != a[j + 1])j = p[j];
		if(a[i + 1] == a[j + 1])j++;
		p[i + 1] = j;
	}
}
int main(){
   while(1){
   	   scanf("%s",a + 1);
   	   if(a[1] == '.')break;
   	   n = strlen(a + 1);
   	   pre();
   	   if(n % (n - p[n]) == 0) printf("%d\n",n / (n - p[n]));
   	   else printf("1\n");
  }
}

Radio Transmission

solution：

结论题
\(ans = n - p[n]\)

/*
  work by:Ariel
*/
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int D = 1e6 + 5;
char a[D];
int p[D], n;
void pre(){
	p[1] = 0;
	for(int i = 1,j = 0;i < n; i++){
	    while(j > 0 && a[i + 1] != a[j + 1])j = p[j];
	    if(a[i + 1] == a[j + 1]) j++;
	    p[i + 1] = j;
	}
}
int main(){
   scanf("%d%s", &n,a + 1);
   pre();
   printf("%d",n - p[n]); 
}