Trie（字典树）

Trie（字典树）

引子

字典树，英文名 Trie。顾名思义，就是一个像字典一样的树。

Trie 树主要用于存储字符串，它的每个节存储一个字符

基本操作

插入 查找 前缀查询 删除

实质：空间换时间

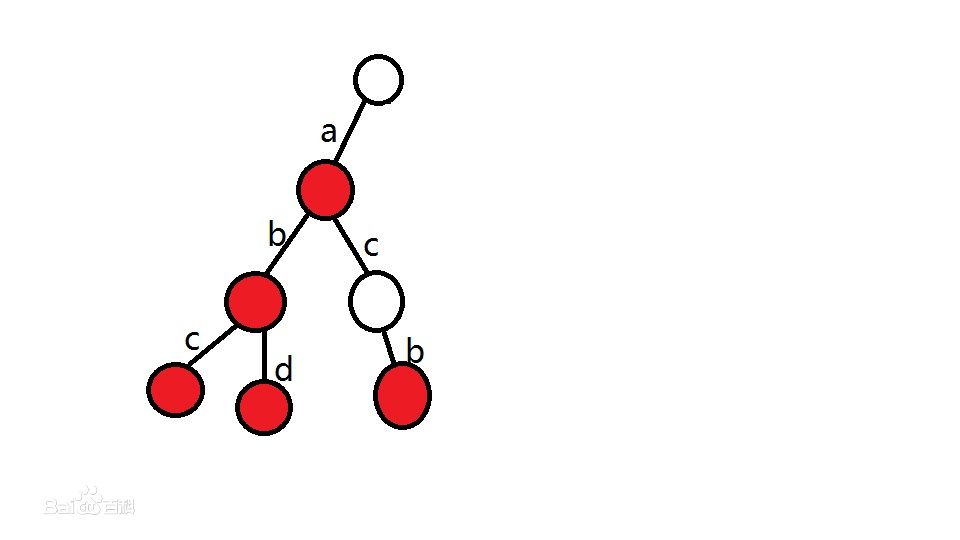
先放图

插入单词：a,ab,abc,abd,acb

应用

- 检索字符串

查找一个字符串是否在字典中出现过

栗题

[于是他错误的点名开始了][1]

给你 \(n\) 个名字串，然后 \(m\) 次点名，每次你需要回答“名字不存在”、“第一次点到这个名字”、“已经点过这个名字”之一
\(n \leq 10^4\), \(1 \leq m \leq 10^5\)

code

/*
work by:Ariel_
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 500010;
int read(){
    int x = 0,f = 1; char c = getchar();
    while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
    return x*f;
}
int n, m;
char s[N];
struct Trie{
   int ch[N][27], val[N], sz;
   Trie() {
   	  sz = 1;
   	  memset(ch[0], 0, sizeof ch[0]);
   	  memset(val, 0, sizeof val);
   }
   int get(char c) {return c - 'a';}
   void Insert(char *s) {
   	  int u = 0, len = strlen(s + 1);
   	  for (int i = 1; i <= len; i++) {
   	  	    int c = get(s[i]);
		    if (!ch[u][c]) {
		    	memset(ch[sz], 0, sizeof ch[sz]);
		    	ch[u][c] = sz++;
			}
			u = ch[u][c]; 
		}
   }
   int Search(char *s) {
   	 int u = 0, len = strlen(s + 1);
   	 for (int i = 1; i <= len; i++) {
   	       int c = get(s[i]);
		   if (!ch[u][c]) return 0;
		   u = ch[u][c];	 
	   }
	  if (!val[u]) {
	  	  val[u] = 1; return 1;
	  }
	  return 2;
   }
}tree;
int main(){
   n = read();
   for (int i = 1; i <= n; i++) scanf("%s", s + 1), tree.Insert(s);
   m = read();
   for (int i = 1; i <= m; i++) {
   	  scanf("%s", s + 1);
   	  int fag = tree.Search(s);
   	  if (fag == 0) printf("WRONG\n");
   	  else if (fag == 1) printf("OK\n");
   	  else if (fag == 2) printf("REPEAT\n");
   } 
   return 0;
}

- AC 自动机

是 AC 自动机的一部分

- 维护异或极值

将数的二进制表示看做一个字符串，就可以建出字符集为 \(\{0,1\}\) 的 trie 树。

栗题

P4551 最长异或路径

给你一棵带边权的树 \((u, v)\)，求 \(u\) 使得 \(v\) 到 \(10^5\) 的路径上的边权异或和最大，输出这个最大值。点数不超过 ，边权在 \([0,2^{31})\) 内

随便找一个根 \(root\)，\(T(u, v)\) 表示 \(u\) 到 \(v\) 路径边权的异或和，那么 很显然 \(T(u, v) = T(root, u) \bigoplus T(root, v)\)

\(T(root, lca(u, v)) 异或两次就被抵消了\)

接下来贪心，从 \(root\) 节点走，如果能向 \((T, u)\) 当前位不同的子树走，那就向那边走

贪心的正确性：如果这么走，这一位为 \(1\) ；如果不这么走，这一位就会为 \(0\)。而高位是需要优先尽量大的

code

/*
work by: Ariel
*/
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;
const int N = 100010;
int read() {
   int x = 0, f = 1; char c = getchar();
   while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
   while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
   return x * f;
}
int n, ch[N << 5][2], tot = 1, ans, dis[N];
struct edge{int v, nxt, w;}e[N << 1];
int head[N], E;
void add_edge(int u, int v, int w) {
   e[++E] = (edge){v, head[u], w};
   head[u] = E;
}
void Insert(int x) {
   for (int i = 30, u = 1; i >= 0; i--) {
   	  int c = ((x >> i) & 1);
   	  if (!ch[u][c]) ch[u][c] = ++tot;
   	  u = ch[u][c];
   }
}
void get(int x) {
   int res = 0;
   for (int i = 30, u = 1; i >= 0; i--) {
   	   int c = ((x >> i) & 1);
   	   if (ch[u][c ^ 1]) {
   	   	   u = ch[u][c ^ 1];
   	   	   res |= (1 << i);
		}
	   else u = ch[u][c];
   }
   ans = max(ans, res);
}
void dfs(int u, int fa) {
    Insert(dis[u]), get(dis[u]);
    for (int i = head[u]; i; i = e[i].nxt) {
    	  int v = e[i].v;
    	  if(v == fa) continue;
    	  dis[v] = dis[u] ^ e[i].w;
    	  dfs(v, u);
	}
}
int main() {
   n = read();
   for (int i = 1, u, v, w; i < n; i++) {
   	   u = read(), v = read(), w = read();
   	   add_edge(u, v, w), add_edge(v, u, w);
   }
   dfs(1, 0);
   printf("%d", ans);
}