题解：AT_abc402_d [ABC402D] Line Crossing

题目中说直线相交，由于这是二维平面，我们可以知道直线要么相交，要么平行，所以我们可以求平行。

观察题目中的这个图，我们可以发现一个性质：

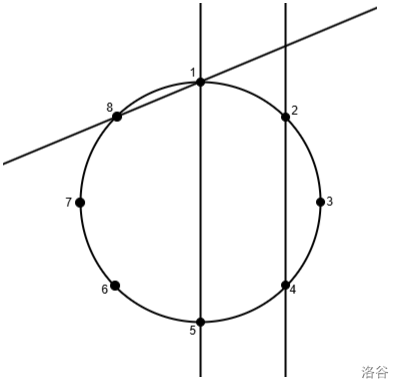
当标号相加的和取余点的个数相同时，这两条直线平行。

知道这个我们就很好做了。

我们可以先开一个数组，下标为模数，数组中的每个数就表示每组平行线的个数。

然后我们只需要枚举平行线的组数，所有的线数减去一组平行线的数量就是与这组平行线相交的线的数量。

由于是求组数，所以简单组合一下就能知道公式。

AC code

#include<bits/stdc++.h>
#define int long long
using namespace std;
int sum[1000003];
int n,m;
int a,b;
signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>a>>b;
		sum[(a+b)%n]++;
	}
	int ans=0;
	for(int i=0;i<n;i++){
		ans+=(m-sum[i])*sum[i];
	}
	cout<<ans/2ll;
}