vp + 补题 + 随机做题记录一

按随机顺序排序

The 2024 ICPC Asia East Continent Online Contest (II) D Query on Tree

link

非常好绝赞8k小清新DS。

0.刚看到题

邻域数点是有经典树分块做法的，但显然不适合竞赛场景。

本题也不是标准的邻域数点，而且邻域范围很小，所以启发我们用一些暴力的做法完成。

1.怎么修改

对于第一种操作，可以差分成两个第二种操作。

所以我们本质上只需要支持邻域加，子树加。

对于邻域加，因为只有 \(k\) 层，所以只需要对每个点维护所有的 \(1\sim 10\) 级子树内子节点，然后每次跳父亲修改，使用 bfs 序就可以做到 \(O(klogn)\) 的单次修改复杂度。

对于子树加，首先可以拆出来 \(10\) 层子树内子节点，做类似邻域的操作（区别在于不需要跳父亲）。

那么对于 \(10\) 层以外的子树内子节点，就不好用邻域操作处理了。

但我们还有 dfs 序，子树的东西很容易想到用 dfs 序连续区间处理。

所以我们额外维护一个邻域加标记 \(t\)，其含义 \(t_x\) 表示 \(x\) 的所有恰好 \(10\) 级子树内子节点的加标记。

形象一点来说，设 \(a_x\) 是用 bfs 序维护的值，\(f_{x,i}\) 表示 \(x\) 的 \(i\) 级祖先，一个点的真实值是 \(a_x+t_{f_{x,10}}\)。

那么继续看 \(10\) 层以外的子树内子节点的修改，他们显然对应到了 \(x\) 子树内除 \(x\) 外所有的 \(t_x\)，因为如果一个点没有任何 \(10\) 级子树内子节点，那么这个点的邻域加标记也是没有意义的。

所以用 dfs 序维护 \(t\)，用 bfs 序维护 \(a\)，我们做到了在 \(O(klogn)\) 的时间内完成修改。

2.怎么查询

我们之所以花大力气维护邻域，就是为了方便邻域的查询。

对于 \(k\) 邻域查询，我们只需要像 \(k\) 邻域修改一样跳父亲，查 \(O(k)\) 个 bfs 序区间最大值和 \(O(k)\) 个 dfs 序单点值即可。

对于恰好 \(k\) 邻域的查询，不能像修改一样做差分，所以我们需要在跳父亲时记录从哪个儿子过来，精细地把儿子的 bfs 序区间剔除，不过总体来看仍然是查询 \(O(k)\) 个 bfs 序区间最大值和 \(O(k)\) 个 dfs 序单点值。

对于子树查询，先把 \(10\) 层邻域做类似上述的邻域查询，接下来考虑 \(10\) 层以外的子树内子节点。

类似加标记，我们不妨把每一层都在 \(10\) 级祖先处统计一下最大值，也就是记录 \(b_x\)，表示 \(x\) 的所有恰好 \(10\) 级子树内子节点的真实值的最大值。

加入我们已经成功维护出来了 \(b\) (显然这个要用 dfs 序维护)，那么我们就可以直接查询 \(x\) 子树内除了 \(x\) 的 \(b_x\) 最大值，与前面 \(10\) 层的值取最大值就是答案。

至此，我们完成了所有查询。

3. \(b\) 怎么维护

考虑修改时都会对 \(b\) 产生什么影响。

修改邻域时，我们取出了 bfs 序的一段区间，这段区间显然对应到唯一的 \(10\) 级祖先，但是这个 \(10\) 级祖先对应的 \(10\) 级子树内子节点可能不止这一段区间的节点。

所以我们先把这个祖先的加标记下放并清空，然后做邻域修改，之后再把新的最大值更新给这个祖先的 \(b\) 值即可。

修改子树时，\(10\) 层的邻域修改需要对 \(b\) 做类似上述邻域修改的操作。

\(10\) 层以外的子树内子节点就直接也给 \(b\) 做一个区间加即可。

至此，我们完成了所有修改。

4.需要干什么

1.预处理

求出每个点的10层子树内邻域是必要的，这个需要 \(O(nk)\) 的时间。

之后是预处理 bfs 序和 dfs 序，同样是 \(O(n+nk)\) 的时间。

2.DS维护

对于 \(a,b,t\)，都需要一个DS去维护，所以我们需要 3 个DS去维护。

对于 \(a\)，需要支持区间加，区间 max。

对于 \(b\)，需要支持区间加，区间 max，单点赋值。

对于 \(t\)，需要支持区间加，单点值，单点赋值。

~~偷懒可以全写线段树~~

5.减少细节讨论

一个比较难处理的点是树高不足时会出现查询不到 \(f_{x,i}\) 的情况。

一种做法是直接分类讨论，查询不到就返回0或者无穷小这类的，不再赘述。

另一种做法是在 1 号节点上面接上足够数量的节点，使得跳父亲一定能跳到确定节点，查祖先也一定能查到确定节点，只需要把额外的节点权值赋为无穷小即可。

我的实现接上去了 20 个节点，肯定是够用的。

6.代码实现

至此，所有的细节都已经讨论完毕，只需要按顺序实现。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=3e5;
const ll inf=1e16, inf2=1e15;
int Test, n, m;
ll a[N];
vector<int> e[N];
int rt;
namespace TREE{
	int f[N][11];
	vector<int> d[N][11];
	inline void dfs(int x, int fa){
		f[x][1]=fa;
		for(auto y:e[x]) if(y^fa) dfs(y, x);
	}
	inline void init(){
		for(int i=1; i<=rt; ++i) for(int j=0; j<=10; ++j) d[i][j].clear(), f[i][j]=0;
		dfs(rt, 0);
		for(int i=1; i<=rt; ++i){
			int x=i;
			for(int j=0; j<=10&&x; ++j){
				d[x][j].emplace_back(i);
				f[i][j]=x;
				x=f[x][1];
			}
		}
	}
};
namespace DS1{
	int que[N], hh, tt;
	ll tr[N<<2], tag[N<<2];
	int bfn[N], seq[N];
	int lb[N][11], rb[N][11];
	inline void build(int p, int l, int r){
		tag[p]=0;
		if(l==r){
			tr[p]=a[seq[l]];
			return ;
		}
		int mid=(l+r)>>1;
		build(p<<1, l, mid); build(p<<1|1, mid+1, r);
		tr[p]=max(tr[p<<1], tr[p<<1|1]);
	}
	inline void push_down(int p){
		if(tag[p]!=0){
			tr[p<<1]+=tag[p]; tag[p<<1]+=tag[p];
			tr[p<<1|1]+=tag[p]; tag[p<<1|1]+=tag[p];
			tag[p]=0;
		}
	}
	inline void add(int p, int l, int r, int L, int R, ll v){
		if(L>R) return ;
		if(L<=l&&r<=R) {
			tag[p]+=v; tr[p]+=v;
			return ;
		}
		int mid=(l+r)>>1;
		push_down(p);
		if(L<=mid) add(p<<1, l, mid, L, R, v);
		if(R>mid) add(p<<1|1, mid+1, r, L, R, v);
		tr[p]=max(tr[p<<1], tr[p<<1|1]);
	}
	inline ll get(int p, int l, int r, int L, int R){
		if(L>R) return -inf;
		if(L<=l&&r<=R) return tr[p];
		int mid=(l+r)>>1;
		push_down(p);
		ll ret=-inf;
		if(L<=mid) ret=max(ret, get(p<<1, l, mid, L, R));
		if(R>mid) ret=max(ret, get(p<<1|1, mid+1, r, L, R));
		return ret;
	}
	inline void init(){
		for(int i=1; i<=rt; ++i) bfn[i]=0;
		que[hh=tt=1]=rt;
		while(hh<=tt){
			int x=que[hh]; bfn[x]=hh; seq[hh]=x; ++hh;
			for(auto y:e[x]) if(!bfn[y]) que[++tt]=y;
		}
		for(int i=1; i<=rt; ++i){
			for(int j=0; j<=10; ++j) {
				lb[i][j]=rt+1; rb[i][j]=0;
				for(auto t:(TREE::d[i][j])){
					lb[i][j]=min(lb[i][j], bfn[t]);
					rb[i][j]=max(rb[i][j], bfn[t]);
				}
			}
		}
		build(1, 1, rt);
	}
};
namespace DS2{
	int dfn[N], out[N], seq[N], timer;
	inline void dfs(int x, int fa){
		dfn[x]=++timer; seq[timer]=x;
		for(auto y:e[x]) if(y^fa){
			dfs(y, x);
		}
		out[x]=timer;
	}
	ll tr[N<<2], tag[N<<2];
	inline void build(int p, int l, int r){
		tag[p]=0;
		if(l==r){
			int cur=seq[l]; tr[p]=-inf;
			for(auto t:(TREE::d[cur][10])){
				tr[p]=max(tr[p], a[t]);
			}
			return ;
		}
		int mid=(l+r)>>1;
		build(p<<1, l, mid); build(p<<1|1, mid+1, r);
		tr[p]=max(tr[p<<1], tr[p<<1|1]);
	}
	inline void push_down(int p){
		if(tag[p]!=0){
			tr[p<<1]+=tag[p]; tag[p<<1]+=tag[p];
			tr[p<<1|1]+=tag[p]; tag[p<<1|1]+=tag[p];
			tag[p]=0;
		}
	}
	inline void set(int p, int l, int r, int x, ll v){
		if(l==r) {
			tr[p]=v;
			return ;
		}
		push_down(p);
		int mid=(l+r)>>1;
		if(x<=mid) set(p<<1, l, mid, x, v);
		else set(p<<1|1, mid+1, r, x, v);
		tr[p]=max(tr[p<<1], tr[p<<1|1]);
	}
	inline void add(int p, int l, int r, int L, int R, ll v){
		if(L>R) return ;
		if(L<=l&&r<=R) {
			tag[p]+=v; tr[p]+=v;
			return ;
		}
		int mid=(l+r)>>1;
		push_down(p);
		if(L<=mid) add(p<<1, l, mid, L, R, v);
		if(R>mid) add(p<<1|1, mid+1, r, L, R, v);
		tr[p]=max(tr[p<<1], tr[p<<1|1]);
	}
	inline ll get(int p, int l, int r, int L, int R){
		if(L>R) return -inf;
		if(L<=l&&r<=R) return tr[p];
		int mid=(l+r)>>1;
		ll ret=-inf;
		push_down(p);
		if(L<=mid) ret=max(ret, get(p<<1, l, mid, L, R));
		if(R>mid) ret=max(ret, get(p<<1|1, mid+1, r, L, R));
		return ret;
	}
	ll tr2[N<<2], tag2[N<<2];
	inline void build2(int p, int l, int r){
		tr2[p]=tag2[p]=0;
		if(l==r) return ;
		int mid=(l+r)>>1;
		build2(p<<1, l, mid); build2(p<<1|1, mid+1, r);
	}
	inline void push_down2(int p){
		if(tag2[p]!=0){
			tr2[p<<1]+=tag2[p]; tag2[p<<1]+=tag2[p];
			tr2[p<<1|1]+=tag2[p]; tag2[p<<1|1]+=tag2[p];
			tag2[p]=0;
		}
	}
	inline void add2(int p, int l, int r, int L, int R, ll v){
		if(L>R) return ;
		if(L<=l&&r<=R){
			tr2[p]+=v; tag2[p]+=v;
			return ;
		}
		int mid=(l+r)>>1;
		push_down2(p);
		if(L<=mid) add2(p<<1, l, mid, L, R, v);
		if(R>mid) add2(p<<1|1, mid+1, r, L, R, v);
	}
	inline void set2(int p, int l, int r, int x, ll v){
		if(l==r){
			tr2[p]=v;
			return ;
		}
		int mid=(l+r)>>1;
		push_down2(p);
		if(x<=mid) set2(p<<1, l, mid, x, v);
		else set2(p<<1|1, mid+1, r, x, v);
	}
	inline ll get2(int p, int l, int r, int x){
		if(l==r) return tr2[p];
		int mid=(l+r)>>1;
		push_down2(p);
		if(x<=mid) return get2(p<<1, l, mid, x);
		else return get2(p<<1|1, mid+1, r, x);
	}
	inline void init(){
		timer=0;
		dfs(rt, 0);
		build(1, 1, rt);
		build2(1, 1, rt);
	}
};
inline void clr(){
	for(int i=1; i<=n+20; ++i) {
		e[i].clear();
	}
}
inline void mdff(int x, int k, int v){
	if(TREE::d[x][k].empty()) return ;
	int p=TREE::d[x][k][0], fp=TREE::f[p][10];
	ll tag=DS2::get2(1, 1, rt, DS2::dfn[fp]);
	DS2::set2(1, 1, rt, DS2::dfn[fp], 0);
	if(tag!=0) DS1::add(1, 1, rt, DS1::lb[fp][10], DS1::rb[fp][10], tag);
	DS1::add(1, 1, rt, DS1::lb[x][k], DS1::rb[x][k], v);
	ll curmx=DS1::get(1, 1, rt, DS1::lb[fp][10], DS1::rb[fp][10]);
	DS2::set(1, 1, rt, DS2::dfn[fp], curmx);
}
inline void mdf(int x, int k, int v){
	while(k>=0){
		mdff(x, k, v);
		if(k-1>=0) mdff(x, k-1, v);
		--k; x=TREE::f[x][1];
	}
}
inline ll gett(int x, int k){
	if(TREE::d[x][k].empty()) return -inf;
	int p=TREE::d[x][k][0], fp=TREE::f[p][10];
	ll tag=DS2::get2(1, 1, rt, DS2::dfn[fp]);
	return tag+DS1::get(1, 1, rt, DS1::lb[x][k], DS1::rb[x][k]);
}
inline ll get(int x, int k){
	ll ret=-inf;
	while(k>=0){
		ret=max(ret, gett(x, k));
		if(k-1>=0) ret=max(ret, gett(x, k-1));
		--k; x=TREE::f[x][1];
	}
	return ret;
}
inline ll get2(int x, int k){
	ll ret=-inf;
	int del=0;
	while(k>=0){
		if(!TREE::d[x][k].empty()){
			if(del&&k-1>=0){
				int p=TREE::d[x][k][0], fp=TREE::f[p][10];
				ll tag=DS2::get2(1, 1, rt, DS2::dfn[fp]);
				int llb=DS1::lb[del][k-1], rrb=DS1::rb[del][k-1];
				if(llb<=rrb) ret=max(ret, tag+max(DS1::get(1, 1, rt, DS1::lb[x][k], llb-1), DS1::get(1, 1, rt, rrb+1, DS1::rb[x][k])));
				else ret=max(ret, tag+DS1::get(1, 1, rt, DS1::lb[x][k], DS1::rb[x][k]));
			}
			else{
				int p=TREE::d[x][k][0], fp=TREE::f[p][10];
				ll tag=DS2::get2(1, 1, rt, DS2::dfn[fp]);
				ret=max(ret, tag+DS1::get(1, 1, rt, DS1::lb[x][k], DS1::rb[x][k]));
			}
		}
		del=x; --k; x=TREE::f[x][1];
	}
	return ret;
}
inline void print(ll x){
	if(x<-inf2) printf("GG\n");
	else printf("%lld\n", x);
}
int main(){
	// freopen("D:\\nya\\acm\\C\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\C\\test.out","w",stdout);
	read(Test);
	while(Test--){
		read(n); read(m);
		clr();
		for(int i=1; i<=n; ++i) read(a[i]);
		for(int i=1, x, y; i<n; ++i){
			read(x); read(y); e[x].emplace_back(y); e[y].emplace_back(x);
		}
		e[n+1].emplace_back(1);
		a[n+1]=-inf;
		for(int i=n+2; i<=n+20; ++i) e[i].emplace_back(i-1), a[i]=-inf;
		rt=n+20;
		TREE::init();
		DS1::init();
		DS2::init();
		int op, x, k, v;
		while(m--){
			read(op); read(x);
			if(op==1){
				read(k); read(v);
				mdf(x, k, v);
				if(k-1>=0) mdf(x, k-1, -v);
				print(get2(x, k));
			}
			else if(op==2){
				read(k); read(v);
				mdf(x, k, v);
				print(get(x, k));
			}
			else {
				read(v);
				for(int t=0; t<=10; ++t){
					mdff(x, t, v);
				}
				DS2::add(1, 1, rt, DS2::dfn[x]+1, DS2::out[x], v);
				DS2::add2(1, 1, rt, DS2::dfn[x]+1, DS2::out[x], v);
				ll ans=DS2::get(1, 1, rt, DS2::dfn[x]+1, DS2::out[x]);
				for(int t=0; t<=10; ++t) ans=max(ans, gett(x, t));
				print(ans);
			}
		}
	}
	return 0;
}

The 3rd Universal Cup. Stage 7: Warsaw C Price Combo

link

非常好的广义矩乘题，很有思维难度。

0.刚看到题

假设没有买一送一，那么每个物品肯定是 \(a_i\) 小去 A 买，\(b_i\) 小去 B 买。

于是我们推论，就算有了买一送一，对于 \(a_i\leq a_j\)，\(b_i\geq b_j\) 的一对物品，一定不会选择在 B 买 \(i\)，在 A 买 \(j\)。

1.转化下形式

我们把所有物品排布在平面上，第 \(i\) 的点放在 \((a_i,b_i)\)。

所以对于某个选在 A 中的点，需要满足其左上方的点全部入选 A 中；对于某个选在 B 中的点，需要满足其右下方的点全部入选 B 中。

这样，我们就把平面用一个从左下到右上的折线划分为两部分阶梯形，所以只需要对这条折线 DP。

2.怎么转移

从左下到右上和从右上到左下都是可以做的，这里仅讨论从右上到左下的扫描线转移方法。

一种策略是维护折线实时的位置，推一下式子会发现需要维护后缀最小值，每次更新是把这个数组向前平移一位，需要平衡树的东西实现，复杂度也是 \(O(nlogn)\)，因为我没写所以不赘述。

另一种策略是考虑对每个点维护折线当前呈现这个样子时，折线覆盖范围（右上角的小矩形）内得到的最小值：

那么对于当前点需要从右上角区域找折线的末端进行连接：

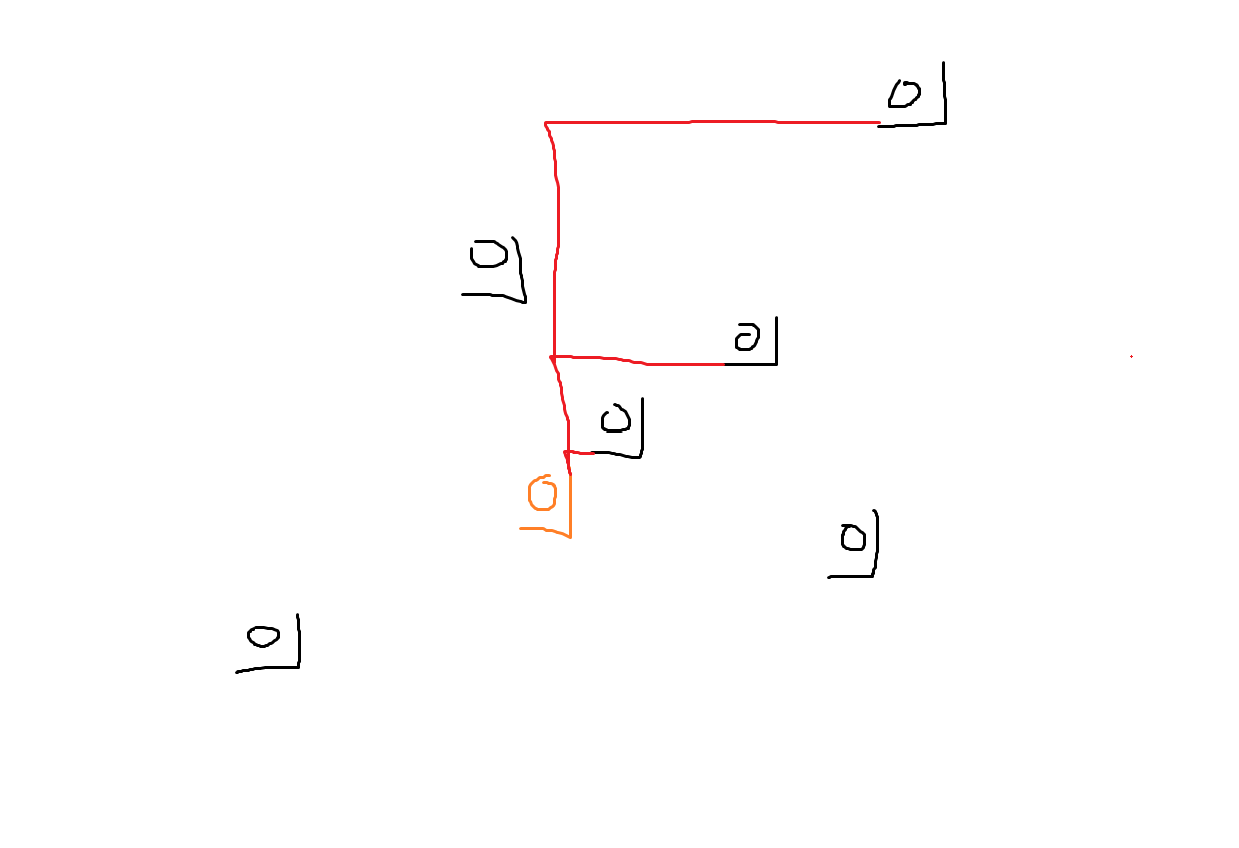
所以我们需要维护每个折线的末端以及转移时需要额外加上的值。

在每个折线末端我们需要维护 4 个值来讨论当前两个区域选择的价值数量的奇偶性，毕竟我们只选择第奇数大的价值算进答案里。

对于选择在 A 中的，那么我们对于其下方的折线末端成乘上一个关于 \(a_i\) 的转移矩阵即可。

对于选择在 B 中的，就棘手一些，我们不能简单的其上方的折线末端乘上一个关于 \(b_i\) 的转移矩阵，因为像图中圈里的这个 \(b\) 可能并不是奇数大中的一员却被我们已经钦定过了。

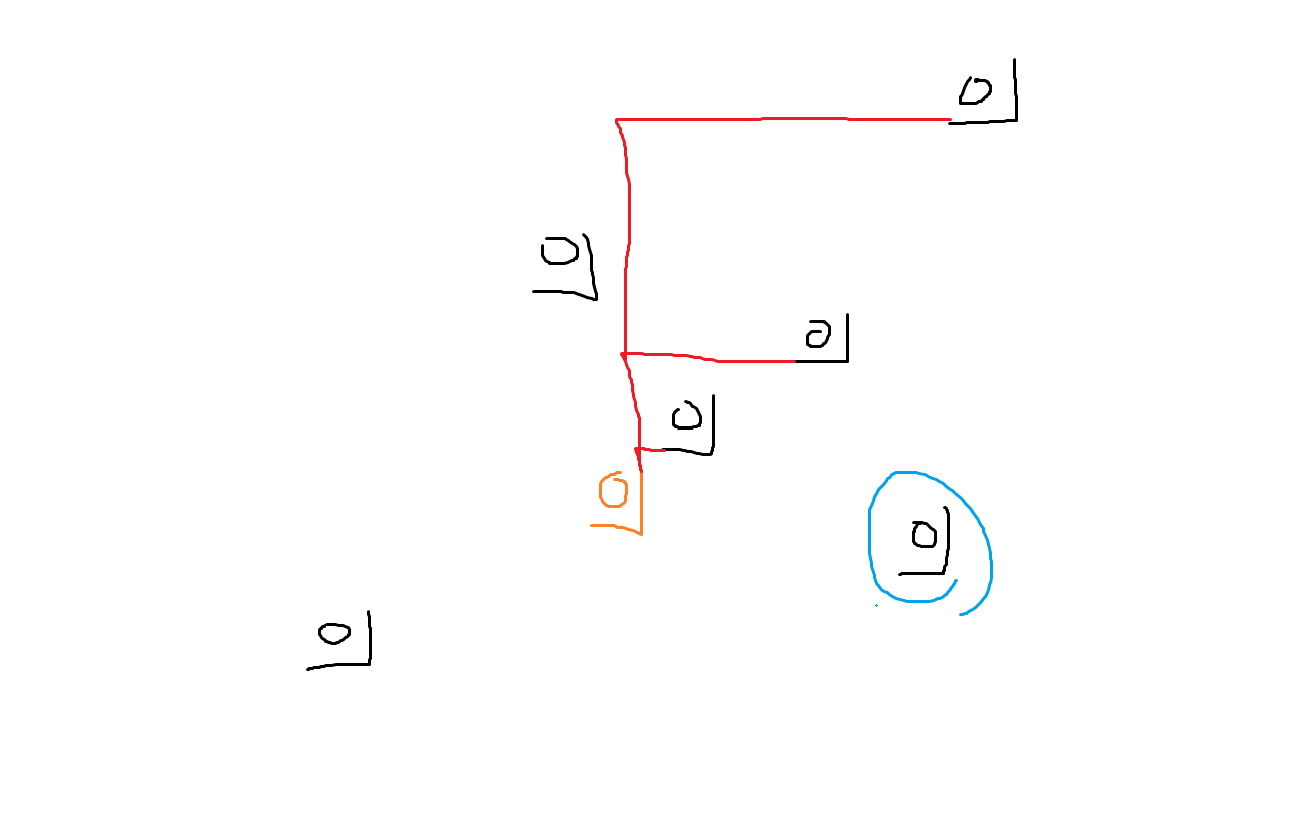
所以我们需要在线段树上维护两个东西，一个就是 dp 矩阵和 A 相关矩阵的乘积，另一个就是区间 B 相关矩阵的乘积，转移时我们需要求 \(f_{k}*g_{k+1,b_i}\) 的最小矩阵，\(f\) 和 \(g\) 就是线段树要维护的东西。

更新时采用类似半在线的方式更新即可。

我直接暴力实现了 \(O(nlogn4^3)\) 的线段树维护矩乘，卡常后可以通过。

代码

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=2e5+5;
const ll inf=1e18;
int n;
int a[N], b[N];
int rka[N], rkb[N], px[N], py[N];
inline bool cmp1(int x, int y){return a[x]<a[y];}
inline bool cmp2(int x, int y){return b[x]<b[y];}
struct mat{
	ll a[4][4];
	int n1, n2;
	mat(){
		for(int i=0; i<4; ++i) for(int j=0; j<4; ++j) a[i][j]=inf;
		n1=4; n2=4;
	}
	inline friend mat operator *(mat x, mat y) {
		mat ret;
		for(int i=0; i<x.n1; ++i){
			for(int j=0; j<y.n2; ++j){
				for(int k=0; k<x.n2; ++k){
					ret.a[i][j]=min(ret.a[i][j], x.a[i][k]+y.a[k][j]);
				}
			}
		}
		ret.n1=x.n1; ret.n2=y.n2;
		return ret;
	}
	inline friend mat operator +(mat x, mat y){
		mat ret;
		for(int i=0; i<4; ++i) for(int j=0; j<4; ++j) ret.a[i][j]=min(x.a[i][j], y.a[i][j]);
		return ret;
	}
	inline friend bool operator !=(mat x, mat y){
		for(int i=0; i<4; ++i) for(int j=0; j<4; ++j) if(x.a[i][j]!=y.a[i][j]) return true;
		return false;
	}
}tr[N<<2], tt[N<<2], tag[N<<2], I, tem, bs;
int idx;
inline void push_up(int p){
	tt[p]=tt[p<<1|1]*tt[p<<1];
	tr[p]=(tr[p<<1|1]*tt[p<<1])+tr[p<<1];
}
inline void build(int p, int l, int r){
	tag[p]=I; tt[p]=I;
	if(l==r){
		tr[p].n1=1; tr[p].n2=4;
		if(l==n+1){
			tr[p].a[0][0]=0;
		}
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1, l, mid); build(p<<1|1, mid+1, r);
	push_up(p);
}
inline void push_down(int p){
	if(tag[p]!=I){
		tr[p<<1]=tr[p<<1]*tag[p]; tag[p<<1]=tag[p<<1]*tag[p];
		tr[p<<1|1]=tr[p<<1|1]*tag[p]; tag[p<<1|1]=tag[p<<1|1]*tag[p];
		tag[p]=I;
	}
}
inline void qry(int p, int l, int r, int L, int R){
	if(L<=l&&r<=R) {
		tem=(tem*tt[p])+tr[p];
		return ;
	}
	int mid=(l+r)>>1;
	push_down(p);
	if(R>mid) qry(p<<1|1, mid+1, r, L, R);
	if(L<=mid) qry(p<<1, l, mid, L, R);
}
inline void mdf(int p, int l, int r, int L, int R){
	if(L>R) return ;
	if(L<=l&&r<=R){
		tr[p]=tr[p]*tem; tag[p]=tag[p]*tem;
		return ;
	}
	int mid=(l+r)>>1;
	push_down(p);
	if(L<=mid) mdf(p<<1, l, mid, L, R);
	if(R>mid) mdf(p<<1|1, mid+1, r, L, R);
	push_up(p);
}
inline void mdf2(int p, int l, int r, int x){
	if(l==r){
		tt[p]=tem;
		return ;
	}
	int mid=(l+r)>>1;
	push_down(p);
	if(x<=mid) mdf2(p<<1, l, mid, x);
	else mdf2(p<<1|1, mid+1, r, x);
	push_up(p);
}
inline void st(int p, int l, int r, int x){
	if(l==r){
		tr[p]=tem;
		return ;
	}
	int mid=(l+r)>>1;
	push_down(p);
	if(x<=mid) st(p<<1, l, mid, x);
	else st(p<<1|1, mid+1, r, x);
	push_up(p);
}
int main(){
	// freopen("D:\\nya\\acm\\C\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\C\\test.out","w",stdout);
	for(int i=0; i<4; ++i) I.a[i][i]=0;
	read(n);
	for(int i=1; i<=n; ++i) read(a[i]);
	for(int i=1; i<=n; ++i) read(b[i]);
	for(int i=1; i<=n; ++i) rka[i]=rkb[i]=i;
	sort(rka+1, rka+n+1, cmp1);
	sort(rkb+1, rkb+n+1, cmp2);
	for(int i=1; i<=n; ++i) px[rka[i]]=i, py[rkb[i]]=i;
	build(1, 0, n+1);
	for(int _=n; _>=0; --_){
		int i=rka[_];
		tem=bs; tem.n1=1; tem.n2=4;
		qry(1, 0, n+1, py[i]+1, n+1);
		st(1, 0, n+1, py[i]);
		mat v1=bs;
		v1.a[1][0]=v1.a[3][2]=0;
		v1.a[0][1]=v1.a[2][3]=b[rkb[py[i]]];
		tem=v1;
		mdf2(1, 0, n+1, py[i]);
		mat v2=bs;
		v2.a[2][0]=v2.a[3][1]=0;
		v2.a[0][2]=v2.a[1][3]=a[i];
		tem=v2;
		mdf(1, 0, n+1, 0, py[i]);
	}
	tem=bs; tem.n1=1; tem.n2=4;
	qry(1, 0, n+1, 0, n+1);
	ll ans=inf;
	for(int i=0; i<4; ++i) ans=min(ans, tem.a[0][i]);
	printf("%lld\n", ans);
	return 0;
}

The 3rd Universal Cup. Stage 10: West Lake F Triangle

link

场切了，写个题解记录下。

0.刚看到题

不妨先把所有字符串按字典序从大到小排序，那么对于 \(i<j<k\)，一定有 \(a_i+a_j>a_k,a_i+a_k>a_j\)。

所以只需要求有多少个 \((j,k)\)，满足 \(a_j+a_k>a_i\) 或 \(a_k+a_j>a_i\)

1.确定 \(a_j+a_k>a_i\) 的数量

假定所有字符串各不相同，那么 \(a_i>a_j\)。

所以 \(a_j+a_k>a_i\) 的必要条件是 \(a_j\) 是 \(a_i\) 的前缀。

不妨考虑暴力怎么写：因为满足 \(a_j\) 是前缀的 \(a_i\) 一定是从 \(j-1\) 向上的一段连续区间，所以暴力枚举这段区间的所有串，查询在所有字符串中最后一个字典序大于 \(a_i-a_j\) 的位置 \(p\)，那么就会给答案贡献 \(\max(p-j, 0)\)。

我们仔细分析一下，所有连续区间的长度是 \(O(n)\)，我们利用二分+hash可以预处理每个字符串的每个后缀的位置 \(p\)。

计算一下二分+hash部分的复杂度，显然只需要算 \(\frac{|S|}{t}\log t \log \frac{|S|}{|t|}\) 的最大值，用 geogebra 画个图发现函数最大值是 \(|S|log|S|\) 左右。

这样即可做到 \(O(n+|S|log|S|)\) 的复杂度。

2.确定 \(a_k+a_j>a_i\) 的数量

同样，需要 \(a_k\) 是 \(a_i\) 的前缀，同样可以用 part 1 的暴力去找 \(a_i\)。

再考虑暴力上的暴力，暴力枚举 \(i<j<k\)，判断可以利用 part 1 的二分+hash做到 \(O(1)\) 判定。

再仔细分析一下，所有连续区间的长度平方之和是 \(O(n^{1.5})\)，所以这一部分也直接暴力做就可以了。

综上，我们用 \(O(n+|S|)\) 的空间和 \(O(n^{1.5}+|S|log|S|)\)的时间解决了本题。

但这个时间复杂度只是很宽的上界，实际表现跑的非常快。

代码

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=3e5+5;
const ull bs=137;
ull pw[1000006];
int Test, n;
char s[1000006];
int id[N], sz[N];
vector<char> str[N];
vector<ull> hs[N];
inline bool cmp(int x, int y){
	int l=1, r=min(sz[x], sz[y]), res=0, mid;
	while(l<=r){
		mid=(l+r)>>1;
		if(hs[x][mid]==hs[y][mid]) {res=mid; l=mid+1;}
		else r=mid-1;
	}
	if(res==min(sz[x], sz[y])) return sz[x]>sz[y];
	return str[x][res+1]>str[y][res+1];
}
vector<int> bd[N];
int pre[N], sam[N];
inline ull get(int id, int l, int r){
	return hs[id][r]-hs[id][l-1]*pw[r-l+1];
}
inline bool chk(int id, int lp, int rp, int cur){
	int l=1, r=min(rp-lp+1, sz[cur]), res=0, mid;
	while(l<=r){
		mid=(l+r)>>1;
		if(get(id, lp, lp+mid-1)==hs[cur][mid]) {res=mid; l=mid+1;}
		else r=mid-1;
	}
	if(res==min(rp-lp+1, sz[cur])) return rp-lp+1<sz[cur];
	return str[id][lp+res]<str[cur][res+1];
}
inline ll calc(int l, int r){
	if(l>r) return 0;
	return (ll)(l+r)*(r-l+1)/2ll;
}
inline ll calc2(int l, int r){
	if(l>r) return 0;
	return (ll)r*(r+1)*(2*r+1)/6ll-(ll)(l-1)*l*(2*l-1)/6ll;
}
int main(){
//	freopen("test.in","r",stdin);
//	freopen("test.out","w",stdout);
	read(Test);
	pw[0]=1;
	for(int i=1; i<=1000000; ++i) pw[i]=pw[i-1]*bs;
	while(Test--){
		read(n);
		for(int i=1; i<=n; ++i){
			scanf("%s", s+1); sz[i]=strlen(s+1);
			hs[i].resize(sz[i]+1); str[i].resize(sz[i]+1); bd[i].resize(sz[i]+2);
			hs[i][0]=0;
			for(int j=1; j<=sz[i]; ++j) hs[i][j]=hs[i][j-1]*bs+s[j], str[i][j]=s[j];
			id[i]=i;
		}
		sort(id+1, id+n+1, cmp);
		ll ans=0;
		for(int l=1, r; l<=n; l=r+1){
			r=l;
			while(r+1<=n&&sz[id[r+1]]==sz[id[l]]&&hs[id[l]][sz[id[l]]]==hs[id[r+1]][sz[id[r+1]]]) ++r;
			pre[r]=l-1;
			sam[r]=r-l+1;
			for(int i=l-1; i>=1; i=pre[i]){
				if(sz[id[i]]<sz[id[l]]) break;
				if(hs[id[i]][sz[id[l]]]!=hs[id[l]][sz[id[l]]]) break;
				ans+=(ll)sam[i]*calc(max(0, bd[id[i]][sz[id[l]]+1]-r), max(0, bd[id[i]][sz[id[l]]+1]-l));
				for(int j=min(bd[id[i]][sz[id[l]]+1], l-1); j>i; j=pre[j]){
					if(sz[id[i]]<sz[id[j]]) {
						ans+=(ll)sam[i]*sam[j]*sam[r]; 
						continue;
					}
					if(hs[id[i]][sz[id[j]]]!=hs[id[j]][sz[id[j]]]) {
						ans+=(ll)sam[i]*sam[j]*sam[r];
						continue;
					}
					if(bd[id[i]][sz[id[j]]+1]<l){
						ans+=(ll)sam[i]*sam[j]*sam[r];
					}
				}
			}
			ans-=calc2(l, r);
			ans-=(ll)sam[r]*l*n;
			ans+=calc(l, r)*(n+l);
			bd[id[r]][sz[id[r]]+1]=n;
			for(int i=sz[id[r]]; i>=1; --i){
				int lp=r+1, rp=n, res=l-1, mid;
				while(lp<=rp){
					mid=(lp+rp)>>1;
					if(chk(id[r], i, sz[id[r]], id[mid])) {res=mid; lp=mid+1;}
					else rp=mid-1;
				}
				bd[id[r]][i]=res;
			}
		}
		printf("%lld\n", ans);
	}
	return 0;
}

upd:怎么大伙都是 SA 啊，怎么我不会 SA 啊。

The 3rd Universal Cup. Stage 10: West Lake B Generated String

link

最不需要SAM的一集

0.刚看到题

我的第一直觉是按长度分治，大串直接做，小串整体做。

但第一眼连所有字符串只是一个区间都不是很好做。

1.只有一个区间怎么做

先考虑上SAM，正串 parent 树很好的性质是子树内节点都以子树根为后缀，于是可以建出正反 SAM，用二维数点做到 \(O(nlog^2n)\)。

但这个做法拓展性不强，如果是多个串的串联，我们可能需要在 parent 树上新建若干横叉边，这会破坏树结构，可能会很不好做。

我们再考虑一个事实：parent 树可以看做子串按字典序排序的结构，根节点代表串的反串的字典序小于等于子树内的代表串的反串字典序。

利用 CDQ 分治，可以去掉时间维度，我们只需要处理离线的静态问题，并不需要在 parent 树上在线搞这个事情。

那么就可以想到把前缀按字典序排序，把后缀按字典序排序，那么每个串能成为前缀串的其他串一定是一段连续的区间。

那么就可以把这个问题转化为二维数点了，于是我们在 CDQ 分治内层做差分二位数点。

分析一下复杂度：

排序：\(O(nlog^2n)\)。CDQ 分治：\(O(nlog^2n)\)。

综上，我们在 \(O(nlog^2n)\) 的时间复杂度内完成了这个简化问题。

2.怎么拓展到原题

如果也能排字典序，那么直接套用上文的 CDQ 分治即可，那么只需要考虑排字典序。

直接用二分+二分排字典序复杂度看似是 \(O(nlog^3n)\)，但实际上可以结合 geogebra 分析，得到还是 \(O(nlog^2n)\) 的。

综上，我们就在 \(O(nlog^2n)\) 的时间内解决了本题，甚至没用上开篇的分治。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=3e5+5;
const int p1=998244353, p2=993244853;
struct hsh{
	int x, y;
	inline hsh operator +(const hsh &t){
		return (hsh){(x+t.x)%p1, (y+t.y)%p2};
	}
	inline hsh operator -(const hsh &t){
		return (hsh){(x-t.x+p1)%p1, (y-t.y+p2)%p2};
	}
	inline hsh operator *(const hsh &t){
		return (hsh){(int)((ll)x*t.x%p1), (int)((ll)y*t.y%p2)};
	}
	inline void operator +=(const hsh &t){
		x=(x+t.x)%p1, y=(y+t.y)%p2;
	}
	inline bool operator ==(const hsh &t){
		return x==t.x&&y==t.y;
	}
}hs[N], bs, pw[N];
int n, m;
char s[N], o[2];
inline hsh get(int l, int r){
	return hs[r]-hs[l-1]*pw[r-l+1];
}
vector<pii> a[N], b[N];
int op[N];
vector<int> lena[N], lenb[N];
vector<hsh> prea[N], preb[N];
inline void init(int x){
	lena[x].emplace_back(0);
	prea[x].emplace_back((hsh){0, 0});
	for(auto t:a[x]) lena[x].emplace_back(lena[x].back()+t.se-t.fi+1), prea[x].emplace_back(prea[x].back()*pw[t.se-t.fi+1]+get(t.fi, t.se));
	lenb[x].emplace_back(0);
	preb[x].emplace_back((hsh){0, 0});
	for(auto t:b[x]) lenb[x].emplace_back(lenb[x].back()+t.se-t.fi+1), preb[x].emplace_back(preb[x].back()*pw[t.se-t.fi+1]+get(t.fi, t.se));
}
inline hsh getsa(int x, int len){
	int l=0, r=lena[x].size()-1, mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(lena[x][mid]<len) ret=mid, l=mid+1;
		else r=mid-1;
	}
	return prea[x][ret]*pw[len-lena[x][ret]]+get(a[x][ret].fi, a[x][ret].fi+(len-lena[x][ret])-1);
}
inline char getssa(int x, int len){
	int l=1, r=lena[x].size()-1, mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(lena[x][mid]<len) ret=mid, l=mid+1;
		else r=mid-1;
	}
	return s[a[x][ret].fi+(len-lena[x][ret])-1];
}
inline bool cmp1(int x, int y){
	int l=1, r=min(lena[x].back(), lena[y].back()), mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(getsa(x, mid)==getsa(y, mid)) {ret=mid, l=mid+1;}
		else {r=mid-1;}
	}
	if(ret==min(lena[x].back(), lena[y].back())){
		if(lena[x].back()==lena[y].back()) return op[x]>op[y];
		return lena[x].back()<lena[y].back();
	}
	return getssa(x, ret+1)<getssa(y, ret+1);
}
inline hsh getsb(int x, int len){
	int l=1, r=lenb[x].size()-1, mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(lenb[x][mid]<len) ret=mid, l=mid+1;
		else r=mid-1;
	}
	return preb[x][ret]*pw[len-lenb[x][ret]]+get(b[x][ret].fi, b[x][ret].fi+(len-lenb[x][ret])-1);
}
inline char getssb(int x, int len){
	int l=1, r=lenb[x].size()-1, mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(lenb[x][mid]<len) ret=mid, l=mid+1;
		else r=mid-1;
	}
	return s[b[x][ret].fi+(len-lenb[x][ret])-1];
}
inline bool cmp2(int x, int y){
	int l=1, r=min(lenb[x].back(), lenb[y].back()), mid, ret=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(getsb(x, mid)==getsb(y, mid)) {ret=mid, l=mid+1;}
		else {r=mid-1;}
	}
	if(ret==min(lenb[x].back(), lenb[y].back())){
		if(lenb[x].back()==lenb[y].back()) return op[x]>op[y];
		return lenb[x].back()<lenb[y].back();
	}
	return getssb(x, ret+1)<getssb(y, ret+1);
}
int rk[N], tt;
int ban[N];
int la[N], ra[N], lb[N], rb[N];
struct node{
	int x, ly, ry, id, val;
}que[N], _que[N];
int tot;
int ans[N];
int tr[N];
inline void add(int x, int v){
	for(; x<=tt; x+=(x&-x)) tr[x]+=v;
}
inline int qry(int l, int r){
	int ret=0;
	for(; r; r-=(r&-r)) ret+=tr[r];
	for(; l; l-=(l&-l)) ret-=tr[l];
	return ret;
}
inline void solve(int l, int r){
	if(l==r) return ;
	int mid=(l+r)>>1;
	solve(l, mid); solve(mid+1, r);
	int lp=l, rp=mid+1, it=l;
	while(lp<=mid||rp<=r){
		if(rp==r+1){
			_que[it]=que[lp]; ++it;
			if(que[lp].id==0) add(que[lp].ly, que[lp].val);
			++lp;
		}
		else if(lp==mid+1){
			_que[it]=que[rp]; ++it;
			if(que[rp].id!=0) ans[que[rp].id]+=qry(que[rp].ly, que[rp].ry)*que[rp].val;
			++rp;
		}
		else if(que[lp].x<=que[rp].x){
			_que[it]=que[lp]; ++it;
			if(que[lp].id==0) add(que[lp].ly, que[lp].val);
			++lp;
		}
		else{
			_que[it]=que[rp]; ++it;
			if(que[rp].id!=0) ans[que[rp].id]+=qry(que[rp].ly, que[rp].ry)*que[rp].val;
			++rp;
		}
	}
	for(int i=l; i<=mid; ++i) if(que[i].id==0) add(que[i].ly, -que[i].val);
	for(int i=l; i<=r; ++i) que[i]=_que[i];
}
int main(){
	// freopen("D:\\nya\\acm\\B\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\B\\test.out","w",stdout);
	read(n); read(m);
	scanf("%s", s+1);
	for(int i=1; i<=n; ++i) s[2*n+1-i]=s[i];
	bs=(hsh){137, 13331};
	pw[0]=(hsh){1, 1};
	for(int i=1; i<=n*2; ++i) hs[i]=hs[i-1]*bs+(hsh){s[i], s[i]}, pw[i]=pw[i-1]*bs;
	int _k, _l, _r;
	for(int i=1; i<=m; ++i){
		scanf("%s", o);
		if(o[0]=='+'){
			read(_k);
			while(_k--){
				read(_l); read(_r); a[i].emplace_back(_l, _r);
			}
			b[i]=a[i];
			reverse(b[i].begin(), b[i].end());
			for(auto &t:b[i]) t.fi=2*n+1-t.fi, t.se=2*n+1-t.se, swap(t.fi, t.se);
			init(i);
			rk[++tt]=i; 
			op[i]=1;
		}
		else if(o[0]=='?') {
			read(_k);
			while(_k--){
				read(_l); read(_r); a[i].emplace_back(_l, _r);
			}
			read(_k);
			while(_k--){
				read(_l); read(_r); b[i].emplace_back(_l, _r);
			}
			reverse(b[i].begin(), b[i].end());
			for(auto &t:b[i]) t.fi=2*n+1-t.fi, t.se=2*n+1-t.se, swap(t.fi, t.se);
			init(i);
			rk[++tt]=i; 
			op[i]=2;
		}
		else {
			read(ban[i]);
		}
	}
	sort(rk+1, rk+tt+1, cmp1);
	for(int i=1; i<=tt; ++i){
		la[rk[i]]=i; 
		int l=i+1, r=tt, mid, ret=i;
		while(l<=r){
			mid=(l+r)>>1;
			if(lena[rk[mid]].back()>=lena[rk[i]].back()&&getsa(rk[mid], lena[rk[i]].back())==prea[rk[i]].back()) {ret=mid; l=mid+1;}
			else {r=mid-1;}
		}
		ra[rk[i]]=ret;
	}
	sort(rk+1, rk+tt+1, cmp2);
	for(int i=1; i<=tt; ++i){
		lb[rk[i]]=i; 
		int l=i+1, r=tt, mid, ret=i;
		while(l<=r){
			mid=(l+r)>>1;
			if(lenb[rk[mid]].back()>=lenb[rk[i]].back()&&getsb(rk[mid], lenb[rk[i]].back())==preb[rk[i]].back()) {ret=mid; l=mid+1;}
			else {r=mid-1;}
		}
		rb[rk[i]]=ret;
	}
	for(int i=1; i<=m; ++i){
		if(op[i]==1){
			que[++tot]=(node){la[i], lb[i], lb[i], 0, 1};
		}
		else if(op[i]==0){
			que[++tot]=(node){la[ban[i]], lb[ban[i]], lb[ban[i]], 0, -1};
		}
		else {
			que[++tot]=(node){la[i]-1, lb[i], rb[i], i, -1};
			que[++tot]=(node){ra[i], lb[i], rb[i], i, 1};
		}
	}
	solve(1, tot);
	for(int i=1; i<=m; ++i) if(op[i]==2) printf("%d\n", ans[i]);
	return 0;
}

The 3rd Universal Cup. Stage 10: West Lake J Sheriruth

link

0.刚看到题

这不是典型找性质缩完点就做完了的题，那就找找性质。

一个点的度数如果大于等于 2，那么他的出边会缩成一个团，如果这个团还有出边，那么出边连向的点同样会缩进这个团内。

于是我们不断缩点，最终会形成每个点只有唯一出边，每个联通块都会最终指向一个团……吗？

这个样例真的给的很良心，我们会发现还有基环树的情况。

于是这个题就需要大力分类讨论了。

1.团

如果起点和终点都不在团里，那么就需要看起点是否在终点子树内，用 dfs 序就可以判断。

如果起点在团里，终点不在团里，那肯定不可达。

如果起点终点都在团里，那么就相当于一共有 \(t\) 个点，我钦定开头结尾分别是给定的起点和终点，中间随便填剩下的点但不能重复，显然这个答案是 \(f(t)=\sum_{i=0}^tC_{t}^ii!\)，有显然的递推式 \(f(t)=t\times f(t-1)+1\)。

如果起点不在团里，终点在团里，那么先找到起点所在子树的根，看一下根和终点是否在原图有边，设 \(sz\) 表示根到团在原图里的边数，\(op=[根和终点在原图有边]\)，那么答案就是 \((sz-op)\times f(|团|-2)+op\)，辅助一个 std::unordered_map 即可求出 \(op\) 。

2.基环树

如果起点和终点都不在环上，那么就需要看起点是否在终点子树内，用 dfs 序就可以判断。

如果起点在环上，终点不在环上，那肯定不可达。

如果起点和终点都在环上，只有唯一一条路径。

如果起点不在环上，终点在环上，那也只有唯一一条路径。

3.处理图

团可以利用 dfs 和并查集处理，处理完后对整张图拓扑排序，没被拓扑排序遍历到的点就是形成基环树森林的点，再对这些点跑反向拓扑序，即可求出环上的点，之后求 dfs 序都是容易的。

总体来看，所有操作都是均摊线性的，我们用 \(O(n+m+q)\) 的时间复杂度和 \(O(n+m)\) 的空间复杂度解决了此问题。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=5e5+5;
int n, m, q, mod;
vector<int> e[N];
int fa[N];
bool inc[N];
inline int get(int x){
	if(x==fa[x]) return x;
	return fa[x]=get(fa[x]);
}
inline void merge(int x, int y){
	x=get(x); y=get(y);
	if(x==y) return ;
	fa[x]=y;
}
inline void dfs(int x, int rt){
	inc[x]=1;
	for(auto y:e[x]) {
		merge(y, rt);
		if(!inc[y]) dfs(y, rt);
	}
}
vector<int> clique[N];
int bel[N];
vector<int> g[N];
int dfn[N], out[N], timer;
int deg[N];
int top[N];
inline void dfs2(int x, int tp){
	dfn[x]=++timer; top[x]=tp;
	for(auto y:g[x]) if(!dfn[y]) dfs2(y, tp);
	out[x]=timer;
}
int pw[N];
unordered_map<ll, bool> h, h2;
inline ll hs(int x, int y){return 1000000000ll*x+y;}
int indeg[N], incir[N];
int fa2[N];
inline int get2(int x){
	if(x==fa2[x]) return x;
	return fa2[x]=get2(fa2[x]);
}
inline void merge2(int x, int y){
	x=get2(x); y=get2(y);
	if(x==y) return ;
	fa2[y]=x;
}
vector<int> cir[N];
int main(){
	// freopen("D:\\nya\\acm\\B\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\B\\test.out","w",stdout);
	read(n); read(m); read(q); read(mod);
	pw[0]=1;
	for(int i=1; i<=n; ++i) pw[i]=((ll)pw[i-1]*i+1)%mod;
	for(int i=1, x, y; i<=m; ++i){
		read(x); read(y); ++x; ++y;
		e[x].ep(y);
		h[hs(x, y)]=1;
	}
	for(int i=1; i<=n; ++i) fa[i]=i;
	for(int i=1; i<=n; ++i) if(e[i].size()>=2&&!inc[i]){
		for(auto t:e[i]) merge(t, e[i][0]), dfs(t, e[i][0]);
	}
	for(int i=1; i<=n; ++i) clique[get(i)].ep(i);
	for(int i=1; i<=n; ++i) if(i==get(i)){
		for(auto t:clique[i]) bel[t]=i;
	}
	for(int i=1; i<=n; ++i){
		for(auto j:e[i]) if(bel[i]^bel[j]){
			if(h2.find(hs(bel[j], bel[i]))==h2.end()){
				g[bel[j]].ep(bel[i]); ++deg[bel[i]]; ++indeg[bel[j]];
				h2[hs(bel[j], bel[i])]=1;
			}
		}
	}
	for(int i=1; i<=n; ++i) if(i==get(i)){
		if(!deg[i]) {
			dfn[i]=++timer;
			for(auto j:g[i]) if(!dfn[j]) dfs2(j, j);
			out[i]=timer;
		}
	}
	queue<int> que;
	for(int i=1; i<=n; ++i) if(!dfn[i]){
		incir[i]=1;
		if(!indeg[i]) que.push(i);
	}
	while(!que.empty()){
		int x=que.front(); que.pop(); incir[x]=0;
		for(auto y:e[x]) if(!(--indeg[y])) que.push(y);
	}
	for(int i=1; i<=n; ++i) fa2[i]=i;
	for(int i=1; i<=n; ++i) if(incir[i]) {
		for(auto j:g[i]) if(incir[j]) merge2(i, j);
	}
	for(int i=1; i<=n; ++i) if(incir[i]) cir[get2(i)].ep(i);
	for(int i=1; i<=n; ++i) if(incir[i]&&get2(i)==i){
		++timer; int cur=timer;
		for(auto t:cir[i]) {
			dfn[t]=cur;
			for(auto tt:g[t]) if(!incir[tt]&&!dfn[tt]) {
				dfs2(tt, tt);
			}
		}
		for(auto t:cir[i]) out[t]=timer;
	}
	while(q--){
		int x, y; read(x); read(y); ++x; ++y;
		if(x==y){
			printf("%d\n", 1%mod);
			continue;
		}
		int fx=get(x), fy=get(y);
		if(dfn[fx]<dfn[fy]||dfn[fx]>out[fy]){
			printf("0\n");
			continue;
		}
		if(incir[fy]){
			printf("%d\n", 1%mod);
			continue;
		}
		if(fx==fy){
			printf("%d\n", pw[clique[fx].size()-2]);
			continue;
		}
		if(clique[fy].size()==1){
			printf("%d\n", 1%mod);
			continue;
		}
		fx=top[fx];
		int sz=e[fx].size();
		int op=h.find(hs(fx, y))!=h.end();
		sz-=op;
		printf("%lld\n", ((ll)sz*pw[clique[fy].size()-2]%mod+op)%mod);
	}
	return 0;
}

The 2nd Universal Cup. Stage 9: Qinhuangdao I Phony

link

~~我就说写线段树分裂是有用的吧~~

0.刚看到题

vp时队友开题提出了按除以 \(k\) 的值分块，按元素数量分治做，大概是 \(n^{1.5}logn\) 之类的东西。

但是想了想感觉直接线段树合并+分裂就是对的，不过复杂度可能是 \(2logn\) 的，空间可能也会炸。

1.细想

需要的操作是把末尾的主席树分裂出一个后缀子树，合并到倒数第二个主席树上，这一部分势能分析是和线段树合并一致的。

但如果不能合并到倒数第二个主席树上，我们就需要把分裂出来的子树作为一棵新主席树，好像势能分析失效了。

但我们细致分析，这种新建操作需要 \(O(logn)\) 分裂出后缀和 \(O(logn)\) 新建，复杂度是严格 \(O(logn)\) 的。

也就是说，总势能并不会发生变化，我们只是用了 \(O(logn)\) 的时间做了不影响势能的操作。

于是总复杂度就是线段树合并复杂度+新建复杂度，总体来看是均摊 \(O(nlogn)\) 的。

2.实现细节

其实只需要注意垃圾空间回收就好。

代码

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=5e5+5;
int n, m; ll K;
struct sgt2{
	int sum[N<<2];
	inline void mdf(int p, int l, int r, int x, int v){
		sum[p]+=v;
		if(l==r) return ;
		int mid=(l+r)>>1;
		if(x<=mid) mdf(p<<1, l, mid, x, v);
		else mdf(p<<1|1, mid+1, r, x, v);
	}
	inline int get(int p, int l, int r, ll &k){
		if(l==r) return l;
		int mid=(l+r)>>1;
		if(sum[p<<1]>=k) return get(p<<1, l, mid, k);
		k-=sum[p<<1];
		return get(p<<1|1, mid+1, r, k);
	}
}T;
int sum[N*80], ls[N*80], rs[N*80];
vector<int> dst;
int rt[N], idx;
inline int gen(){
	if(!dst.empty()){
		int x=dst.back();
		sum[x]=ls[x]=rs[x]=0;
		dst.pop_back();
		return x;
	}
	return ++idx;
}
vector<ll> vec;
ll a[N], p[N], r[N];
vector<ll> lis;
int len;
inline ll get(int p, int l, int r, int k){
	if(l==r) return lis[l];
	int mid=(l+r)>>1;
	if(sum[ls[p]]>=k) return get(ls[p], l, mid, k);
	return get(rs[p], mid+1, r, k-sum[ls[p]]);
}
inline void ins(int &p, int l, int r, int x){
	if(!p) p=gen();
	++sum[p];
	if(l==r) return ;
	int mid=(l+r)>>1;
	if(x<=mid) ins(ls[p], l, mid, x);
	else ins(rs[p], mid+1, r, x);
}
inline void merge(int &p, int &q, int l, int r, int k){
	if(!q) return ;
	if(!p) {
		if(sum[q]==k) {
			p=q; q=0;
			return ;
		}
		else p=gen();
	}
	if(l==r){
		assert(sum[q]>=k);
		sum[q]-=k; sum[p]+=k;
		if(sum[q]==0) dst.ep(q), q=0;
		return ;
	}
	int mid=(l+r)>>1;
	if(sum[rs[q]]>=k) merge(rs[p], rs[q], mid+1, r, k);
	else {
		k-=sum[rs[q]];
		merge(rs[p], rs[q], mid+1, r, sum[rs[q]]);
		merge(ls[p], ls[q], l, mid, k);
	}
	sum[p]=sum[ls[p]]+sum[rs[p]];
	sum[q]=sum[ls[q]]+sum[rs[q]];
	if(sum[p]==0) dst.ep(p), p=0;
	if(sum[q]==0) dst.ep(q), q=0;
}
inline void work(int k){
	if(!k) return ;
	if(vec.size()==1||vec[vec.size()-2]!=vec.back()-1){
		ll lst=vec.back(); vec.pop_back();
		vec.push_back(lst-1); vec.push_back(lst);
		T.mdf(1, 0, n-1, vec.size()-1, sum[rt[vec.size()-2]]);
		T.mdf(1, 0, n-1, vec.size()-2, -sum[rt[vec.size()-2]]);
		rt[vec.size()-1]=rt[vec.size()-2]; rt[vec.size()-2]=0;
	}
	T.mdf(1, 0, n-1, vec.size()-2, k); 
	T.mdf(1, 0, n-1, vec.size()-1, -k);
	merge(rt[vec.size()-2], rt[vec.size()-1], 0, len, k);
	if(sum[rt[vec.size()-1]]==0) {
		vec.pop_back();
	}
}
int main(){
//	freopen("test.in","r",stdin);
//	freopen("test2.out","w",stdout);
	read(n); read(m); read(K);
	for(int i=1; i<=n; ++i) read(a[i]), p[i]=a[i]/K, r[i]=a[i]%K, vec.ep(p[i]), lis.ep(r[i]);
	sort(vec.begin(), vec.end());
	vec.erase(unique(vec.begin(), vec.end()), vec.end());
	sort(lis.begin(), lis.end());
	lis.erase(unique(lis.begin(), lis.end()), lis.end());
	len=lis.size()-1;
	for(int i=1; i<=n; ++i) r[i]=lower_bound(lis.begin(), lis.end(), r[i])-lis.begin();
	for(int i=1; i<=n; ++i){
		int id=lower_bound(vec.begin(), vec.end(), p[i])-vec.begin();
		ins(rt[id], 0, len, r[i]);
	}
	for(int i=0; i<(int)vec.size(); ++i) T.mdf(1, 0, n-1, i, sum[rt[i]]);
	ll pre=0;
	while(m--){
		char op=getchar();
		while(op!='A'&&op!='C') op=getchar();
		ll x; read(x);
		if(op=='C'){
			pre+=x;
		}
		else{
			swap(pre, x);
			while(x){
				if(vec.size()==1){
					if(x%n==0){
						vec[0]-=x/n;
						x=0;
					}
					else{
						vec[0]-=x/n;
						x%=n;
						work(x); x=0;
					}
				}
				else{
					int dt=sum[rt[vec.size()-1]];
					if(x>=(vec.back()-vec[vec.size()-2])*dt){
						x-=(vec.back()-vec[vec.size()-2])*dt;
						T.mdf(1, 0, n-1, vec.size()-2, dt); 
						T.mdf(1, 0, n-1, vec.size()-1, -dt);
						merge(rt[vec.size()-2], rt[vec.size()-1], 0, len, dt);
						vec.pop_back();
						continue;
					}
					if(vec.back()-(x/dt)<=vec[vec.size()-2]){
						x-=(vec.back()-vec[vec.size()-2]-1)*dt;
						vec.back()=vec[vec.size()-2]+1;
					}
					else{
						vec.back()-=x/dt;
						x%=dt;
					}
					if(x>sum[rt[vec.size()-1]]) x-=sum[rt[vec.size()-1]], work(sum[rt[vec.size()-1]]);
					else work(x), x=0;
				}
			}
			x=pre;
			x=n-x+1;
			int currt=T.get(1, 0, n-1, x);
			printf("%lld\n", K*vec[currt]+get(rt[currt], 0, len, x));
			pre=0;
		}
	}
	return 0;
}

3.bonus

如果有第三种操作是不断给最小值 \(+k\)，还能做吗？

（答案是肯定的，势能分析类似，不过实现细节会多很多，可以利用贪玩蓝月那题的结论取代 std::deque 减少一些实现细节，毕竟只需要改变根的位置而不是真的交换主席树。）

The 2nd Universal Cup. Stage 9: Qinhuangdao C Palindrome

link

场上完全能做出来的题却因为忘了回文自动机的性质遗憾没开。

0.刚看到题

队友开的，显然可以把区间最长的对称前后缀去掉，这个用二分+hash可以做到 \(O(logn)\)。

如果恰好删完，那就输出 0 0。

否则求剩下区间前缀和后缀最长回文串，这个场上唐了忘了咋用PAM。

两者取最大，可以得到要删除的区间。

假设要删的是 \([lp, rp]\)，那么答案就是 \(1+lcp(s[lp, r], s[rp+1, r])+lcs(s[l, rp], s[l, lp-1])\)，其中 \(p\) 指前缀，\(s\) 指后缀。这个同样可以用二分+hash做。

一点细节是前后缀最长回文串相等的话，要么就是整个剩下的区间，要么两个串互不影响，都统计一下答案加起来就好。

那么只剩下求固定端点的区间最长回文串。

1.PAM

（这个 part 仅仅是为了提醒未来的自己 PAM 的性质）

正串 PAM 的 fail 指针含义是代表串的最长回文后缀，那么就可以类比 SAM，用倍增就可以 \(O(logn)\) 求答案。

那么只需要维护正反串 PAM 就可以了。

为了记忆方便其实只需要知道 PAM 是类比 SAM 搭建的，毕竟原作者论文里就直接这么说的。

那么这题就做完了。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=5e5+5;
int n, m;
char s[N];
struct node{
	int ch[26];
	int fail,len,num;
};
struct PAM{
	node a[N];
	int lst,cnt;
	PAM(){
		a[0].len=0;a[0].fail=1;
		a[1].len=-1;a[1].fail=0;
		lst=0;cnt=1;
	}
	int get_fail(int x,int lim){
		while(s[lim-a[x].len-1]!=s[lim]) x=a[x].fail;
		return x;
	}
	void insert(int c,int lim){
		int p=get_fail(lst,lim);
		if(!a[p].ch[c]){
			a[++cnt].len=a[p].len+2;
			int q=get_fail(a[p].fail,lim);
			a[cnt].fail=a[q].ch[c];
			a[cnt].num=a[a[cnt].fail].num+1;
			a[p].ch[c]=cnt;
		}
		lst=a[p].ch[c];
	}
    int pos[N];
    int f[N][20];
	void init(){
		for(int i=1;i<=n;i++){
			insert(s[i]-'a',i); pos[i]=lst;
		}
        for(int i=2; i<=cnt; ++i) f[i][0]=a[i].fail;
        for(int t=1; t<=19; ++t) for(int i=2; i<=cnt; ++i) f[i][t]=f[f[i][t-1]][t-1];
	}
}p1, p2;
const int mod1=998244353, mod2=993244853;
inline pii operator +(pii x, pii y){
    return mapa((x.fi+y.fi)%mod1, (x.se+y.se)%mod2);
}
inline pii operator -(pii x, pii y){
    return mapa((x.fi-y.fi+mod1)%mod1, (x.se-y.se+mod2)%mod2);
}
inline pii operator *(pii x, pii y){
    return mapa(((ll)x.fi*y.fi)%mod1, ((ll)x.se*y.se)%mod2);
}
pii hs[N], pw[N], hs2[N];
pii bs=mapa(131, 13331);
inline pii get(int l, int r){
    return hs[r]-hs[l-1]*pw[r-l+1];
}
inline pii get2(int l, int r){
    l=n-l+1; r=n-r+1; swap(l, r);
    return hs2[r]-hs2[l-1]*pw[r-l+1];
}
int main(){
	// freopen("D:\\nya\\acm\\A\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\A\\test.out","w",stdout);
    read(n);
    scanf("%s", s+1);
    p1.init();
    reverse(s+1, s+n+1);
    p2.init();
    reverse(s+1, s+n+1);
    pw[0]=mapa(1, 1);
    for(int i=1; i<=n; ++i) hs[i]=hs[i-1]*bs+mapa(s[i], s[i]), pw[i]=pw[i-1]*bs;
    reverse(s+1, s+n+1);
    for(int i=1; i<=n; ++i) hs2[i]=hs2[i-1]*bs+mapa(s[i], s[i]);
    // reverse(s+1, s+n+1);
    read(m);
    while(m--){
        int l, r; read(l); read(r);
        // for(int i=l; i<=r; ++i) putchar(s[i]);
        // putchar('\n');
        int lp=1, rp=(r-l+1)/2, mid, ret=0, res;
        while(lp<=rp){
            mid=(lp+rp)>>1;
            if(get(l, l+mid-1)==get2(r-mid+1, r)) {ret=mid; lp=mid+1;}
            else rp=mid-1;
        }
        if(ret*2==r-l+1){
            printf("0 0\n");
            continue;
        }
        int lim=r-l+1-ret*2;
        int px=p1.pos[r-ret];
        for(int i=19; i>=0; --i) if(p1.a[p1.f[px][i]].len>=lim) px=p1.f[px][i];
        if(p1.a[px].len>lim) px=p1.f[px][0];
        int py=p2.pos[n-(l+ret)+1];
        for(int i=19; i>=0; --i) if(p2.a[p2.f[py][i]].len>=lim) py=p2.f[py][i];
        if(p2.a[py].len>lim) py=p2.f[py][0];
        int len1=p1.a[px].len, len2=p2.a[py].len;
        if(len1==lim){
            printf("0 0\n");
            continue ;
        }
        int d1, d2;
        if(len1>len2) d2=r-ret-len1, d1=l+ret;
        else d2=r-ret, d1=l+ret+len2;
        int ans=1;
        lp=1, rp=d1-l, res=0;
        while(lp<=rp){
            mid=(lp+rp)>>1;
            if(get(d1-1-mid+1, d1-1)==get(d2-mid+1, d2)) {res=mid; lp=mid+1;}
            else rp=mid-1;
        }
        ans+=res;
        lp=1, rp=r-d2, res=0;
        while(lp<=rp){
            mid=(lp+rp)>>1;
            if(get(d1, d1+mid-1)==get(d2+1, d2+mid)) {res=mid; lp=mid+1;}
            else rp=mid-1;
        }
        ans+=res;
        if(len1==len2){
            ++ans;
            d2=r-ret-len1, d1=l+ret;
            lp=1, rp=d1-l, res=0;
            while(lp<=rp){
                mid=(lp+rp)>>1;
                if(get(d1-1-mid+1, d1-1)==get(d2-mid+1, d2)) {res=mid; lp=mid+1;}
                else rp=mid-1;
            }
            ans+=res;
            lp=1, rp=r-d2, res=0;
            while(lp<=rp){
                mid=(lp+rp)>>1;
                if(get(d1, d1+mid-1)==get(d2+1, d2+mid)) {res=mid; lp=mid+1;}
                else rp=mid-1;
            }
            ans+=res;
        }
        printf("%d %d\n", lim-max(len1, len2), ans);
    }
    return 0;
}

The 2nd Universal Cup. Stage 9: Qinhuangdao H Quake and Rebuild

link

讲一下不同于官方题解的卡常做法，实现还算比较简单。

0.刚看到题

虚树大小比较容易想到"按 dfs 序排序，加上相邻点距离，除以 2 加 1 "的结论。

那么先考虑怎么求 lca，传统的方法大概都失效了。

还有的问题是怎么求 dfs 序，毕竟没有 dfs 序就很难建虚树。

包括求答案甚至都是不能做的，毕竟每个点的深度也在动态变化。

一步一步入手。

1.怎么求 lca

但这题的树有到根的路径编号递减的性质，也就是说在序列上只会向左跳，所以类似倍增的东西仍然是可以参考的。

考虑序列分治，设阈值 \(B\)，块内维护每个点第一个跳到块外的祖先，记作 \(nxt_i\)。

有了这个，我们可以类似倍增 lca，在 \(O(\frac{n}{B})\) 的时间内先让两个点跳到 \(nxt\) 相同的地方。

再分类讨论，如果二者在同一个块，那就可以直接 \(O(B)\) 暴力找 lca，否则 lca 就直接是两个点共同的 \(nxt\)。

2.怎么维护 \(nxt\)

容易发现，如果一个块被减的数量超过了块长，那么每个点的父亲就是 \(nxt\)，所以每个块只需要维护 \(O(B)\) 次整块减。

对于散块，直接暴力重构就好。

那么维护 \(nxt\) 的复杂度就是 \(O(\frac{n}{B}\times B^2+nB)\)，查询 lca 单次复杂度为 \(O(B+\frac{n}{B})\)，取 \(B=\sqrt n\) 最优。

3.怎么求 dfs 序

好像很困难，但想想我们为什么要用 dfs 序。

其实只需要能够比较两个点的相对 dfs 序即可，这个可以倍增到 lca 前的一个节点实现，我们按照邻居从小到大决定 dfs 序，那么就可以在 \(O(\frac{n}{B}+B)\) 的时间内比较两个点的相对 dfs 序。

但是我们外层是排序，所以这一部分是 \(O(\sum{k}log k\sqrt n)\) 的，很难受，但还算能接受。

4.怎么求深度

这个其实很好解决，在维护 \(nxt\) 的同时维护跳出块需要的最少步数，那么就可以用 \(O(B+\frac{n}{B})\) 的时间求出某个点的深度了。

至此，我们在 \(O(n\sqrt n+\sum{k}log k\sqrt n)\) 的时间内解决了本题……吗？

很不幸，这个做法过不去。

5.卡常？

最大瓶颈在于排序，但目前好像没有不依赖比较 dfs 序的虚树构建方法。

考虑用堆减少比较次数，反而更慢了。

似乎走投无路了？

6.再分治！

很容易想到这个做法是被点数很多的询问卡的，所以我们想一想怎么去解决大询问。

这时候我们很容易想到一个暴力做法：从大到小枚举，如果一个点在虚树内并且不是公共 lca，那么就在答案统计一个点，把这个点跳到父亲。

这个做法是单次询问 \(O(n)\) 的，所以可以很好的解决大询问的问题。

那么设阈值为 \(B_2\)，那么小询问复杂度为 \(O(\sum k\sqrt nlogB_2)\)，大询问复杂度为 \(O(\frac{\sum{k}}{B_2}n)\)，肯定是要少于 \(O(\sum klogk\sqrt n)\) 的。

我实现时取了 \(B_2=600\)，可以通过。

代码

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=2e5+5;
const int B=600;
int n, m;
int lp[B], rp[B], bid[N];
int fa[N], nxt[N], dis[N];
int ins[N];
int dt[B];
inline void rebuild(int i){
	if(dt[i]>=B) return ;
	for(int j=lp[i]; j<=rp[i]; ++j){
		int x=j; dis[j]=0;
		while(x>=lp[i]) ++dis[j], x=max(1, fa[x]-dt[i]);
		nxt[j]=x;
	}
}
#define gf(x) (dt[bid[x]]<B?nxt[x]:max(1, fa[x]-dt[bid[x]]))
inline int lca(int x, int y){
	while(gf(x)^gf(y)){
		if(x<y) y=gf(y);
		else x=gf(x);
	}
	if(bid[x]!=bid[y]) return gf(x);
	while(x^y){
		if(x<y) y=max(1, fa[y]-dt[bid[y]]);
		else x=max(1, fa[x]-dt[bid[x]]);
	}
	return x;
}
inline int dep(int x){
	int ret=0;
	while(x^1){
		if(dt[bid[x]]<B) ret+=dis[x], x=nxt[x];
		else ++ret, x=max(1, fa[x]-dt[bid[x]]);
	}
	return ret;
}
inline int getd(int x, int y){
	if(x==y) return 0;
	return dep(x)+dep(y)-2*dep(lca(x, y));
}
inline int jump(int x, int t){
	while(true) {
		while(gf(x)>t) x=gf(x);
		if(max(1, fa[x]-dt[bid[x]])>t) x=max(1, fa[x]-dt[bid[x]]);
		else return x;
	}
}
inline bool cmp(int x, int y){
	if(x==y)  return false;
	int t=lca(x, y);
	if(t==x) return true;
	if(t==y) return false;
	return jump(x, t)<jump(y, t);
}
bool occ[N];
int main(){
	// freopen("D:\\nya\\acm\\B\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\B\\test.out","w",stdout);
	read(n); read(m);
	for(int i=2; i<=n; ++i) read(fa[i]);
	for(int i=2; i<=n; ++i) bid[i]=(i-2)/B+1;
	bid[1]=0; 
	lp[0]=rp[0]=1; dt[0]=B;
	for(int i=1; i<=bid[n]; ++i) lp[i]=rp[i-1]+1, rp[i]=rp[i-1]+B;
	rp[bid[n]]=n;
	for(int i=1; i<=bid[n]; ++i) rebuild(i);
	while(m--){
		int op; read(op);
		if(op==1){
			int l, r, d; read(l); read(r); read(d);
			if(bid[l]==bid[r]){
				for(int i=l; i<=r; ++i) fa[i]-=d, fa[i]=max(fa[i], 0);
				rebuild(bid[l]);
				continue;
			}
			for(int i=l; i<=rp[bid[l]]; ++i) fa[i]-=d, fa[i]=max(fa[i], 0);
			rebuild(bid[l]);
			for(int i=lp[bid[r]]; i<=r; ++i) fa[i]-=d, fa[i]=max(fa[i], 0);
			rebuild(bid[r]);
			for(int i=bid[l]+1; i<bid[r]; ++i){
				dt[i]+=d; dt[i]=min(dt[i], n); rebuild(i);
			}
		}
		else{
			int k, x; 
			read(k);
			if(k==0){
				printf("0\n");
				continue;
			}
			vector<int> vec;
			while(k--){
				read(x); if(!ins[x]) vec.ep(x), ins[x]=1;
			}
			if(vec.size()>=B){
				int lc=vec[0];
				for(auto t:vec) lc=lca(lc, t);
				int ans=1;
				for(int i=n; i>lc; --i) if(ins[i]) ++ans, ins[max(1, fa[i]-dt[bid[i]])]=1, ins[i]=0;
				ins[lc]=0;
				printf("%d\n", ans);
				continue;
			}
			sort(vec.begin(), vec.end(), cmp);
			vec.ep(vec[0]);
			int ans=0;
			for(int i=1; i<(int)vec.size(); ++i) ans+=getd(vec[i-1], vec[i]);
			ans>>=1;
			for(auto t:vec) ins[t]=0;
			printf("%d\n", ans+1);
		}
	}
	return 0;
}

The 3rd Universal Cup. Stage 12: Qinhuangdao K Diversity and Variance

link

~~喜欢最小化字典序和卡行末空格的÷↑们，你们好，中间忘了，小米Su7创死你。~~

0.刚看到题

队友开的，显然是排序后只会取一段前缀和一段后缀，利用方差和平均数的转换就可以维护最大方差。

但是，

那么就变得很困难了。

1.怎么比较字典序。

联想到二分+hash比较字典序的方法，我们可以用可持久化线段树维护值域区间下标的存在情况，因为这题相当于要维护的字符串是个排列，所以可以用随机化异或来判断某个值域区间是否相同。

那么只需要在遍历前缀时维护可持久化线段树即可……吗？

2.怎么处理重复的 \(a_i\)

我们上述讨论的只在所有 \(a_i\) 互不相同时才行，如果存在重复的 \(a_i\)，那么后缀最前面那段 \(a\) 应该换到下标更小的。

不过这个也是容易解决的，利用两个 std::priority_queue ，每次从前缀中弹出最大的加入后缀，再从后缀中找到值最大下标最小的更新，就可以解决重复段选靠前的问题。

3.细节

只让选一个数那就直接输出 1。

然后，

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
typedef unsigned int uint;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=1e5+5;
int TEST, n, m;
pii a[N];
mt19937 rnd(time(0));
uint val[N];
int rt[N], idx;
uint hs[N*100]; int ls[N*100], rs[N*100];
inline void ins(int &p, int q, int l, int r, int x){
	p=++idx; hs[p]=hs[q]; ls[p]=ls[q]; rs[p]=rs[q];
	if(l==r){
		hs[p]^=val[x];
		return ;
	}
	int mid=(l+r)>>1;
	if(x<=mid) ins(ls[p], ls[q], l, mid, x);
	else ins(rs[p], rs[q], mid+1, r, x);
	hs[p]=hs[ls[p]]^hs[rs[p]];
}
inline bool cmp(int p, int q, int l, int r){
	if(l==r){
		return hs[p]>hs[q];
	}
	int mid=(l+r)>>1;
	if(hs[ls[p]]^hs[ls[q]]) return cmp(ls[p], ls[q], l, mid);
	return cmp(rs[p], rs[q], mid+1, r);
}
vector<int> res;
inline void dfs(int p, int l, int r){
	if(!hs[p]) return ;
	if(l==r) {
		res.ep(l); return ;
	}
	int mid=(l+r)>>1;
	dfs(ls[p], l, mid); dfs(rs[p], mid+1, r);
}
int main(){
	// freopen("D:\\nya\\acm\\A\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\A\\test.out","w",stdout);
	read(TEST);
	while(TEST--){
		read(n); read(m); m=n-m;
		for(int i=1; i<=n; ++i) read(a[i].fi), a[i].se=i, val[i]=rnd();
		if(m==n){
			for(int i=1; i<n; ++i) printf("%d ", i);
			printf("%d\n", n);
			continue;
		}
		if(m==1){
			printf("1\n");
			continue;
		}
		sort(a+1, a+n+1);
		idx=0;
		priority_queue<pii, vector<pii> > pq1;
		ll sum1=0, sum2=0;
		for(int i=1; i<=m; ++i) sum1+=a[i].fi, sum2+=a[i].fi*a[i].fi, pq1.push(mapa(a[i].fi, a[i].se));
		priority_queue<pii, vector<pii> > pq2;
		for(int i=m+1; i<=n; ++i) pq2.push(mapa(a[i].fi, -a[i].se));
		ll mx=sum2*m-sum1*sum1; int id=m;
		rt[m]=0;
		for(int i=1; i<=m; ++i) ins(rt[m], rt[m], 1, n, a[i].se);
		for(int i=m-1; i>=0; --i){
			pii tp=pq1.top(); pq1.pop();
			ins(rt[i], rt[i+1], 1, n, tp.se);
			sum2-=tp.fi*tp.fi; sum1-=tp.fi;
			tp.se=-tp.se;
			pq2.push(tp);
			tp=pq2.top(); pq2.pop();
			ins(rt[i], rt[i], 1, n, -tp.se);
			sum2+=tp.fi*tp.fi; sum1+=tp.fi;
			if(sum2*m-sum1*sum1>mx){
				mx=sum2*m-sum1*sum1;
				id=i;
			}
			else if(sum2*m-sum1*sum1==mx){
				if(cmp(rt[i], rt[id], 1, n)) id=i;
			}
		}
		res.clear();
		dfs(rt[id], 1, n);
		for(int i=0; i<(int)res.size()-1; ++i) printf("%d ", res[i]);
		printf("%d\n", res.back());
	}
	return 0;
}

The 3rd Universal Cup. Stage 13: Sendai G Count Pseudo-Palindromes

link

~~"这不是暴力吗？"~~

~~"？怎么过了？"~~

0.刚看到题

判断一个区间是否每个数都出现偶数次显然可以用随机异或 hash，这题保证每个数只出现两次，如果继续随机异或 hash 的思路无疑是在加强问题。

所以更合理的应该是从每种颜色的左下标和右下标出发去考虑。

1.先构造点极端情况

一个位置的合法区间数量最坏是 \(O(n^2)\) 的，考虑类似 6 6 5 5 4 4 1 2 2 3 3 1 的数据。

但是我们发现如果不考虑左右下标都在一侧的情况，本质不同的极小合法区间只有 1 自己。

所以我们大胆猜测，本质不同的极小合法区间并不多。

2.如果能求极小合法区间

那么我们暴力枚举每个极小合法区间，考虑左右端点分别还能延伸多长。

我们预处理一下每个位置往左/右最少延长多少个得到一个随机异或 hash 为 0 的位置，那么显然如果有更长的位置可以由两个本质相同的区间拼接起来。

所以这本质上类似一个传递闭包的 dag 最长链，直接开个 hash 表 (std::unordered_map) 线性扫一遍即可。

这样枚举每个极小合法区间，能以此为基础组成的合法区间数量就是（左端点左最长链长度）乘（右端点右最长链长度）。

所以如果能求出来所有极小合法区间，剩下的问题可以在线性时间内解决。

3.怎么求极小合法区间

观察到对于两个左端点 \(i,j(i<j)\)，如果两个左端点都能找到合法的右端点 \(r_i,r_j\)，那么一定有 \(r_i>r_j\)。

所以这是一个不断向外扩展的区间，我们就从 \((i,i)\) 开始扩展。

因为我们要求极小合法区间，所以我们每次调左/右端点时，不能出现左/右从头开始有连续的随机异或 hash 为 0 的区间。

所以我们再预处理一下每个位置应该扩展到哪里，这个也可以用 hash 表线性扫一遍解决。

然后还需要不断调整，扩展到区间内左端点最小值/右端点最大值，这个可以用 st 表解决。

所以我们需要 \(O(n+nlogn)\) 的时间预处理，\(O(暴力跳的步数\times st 表常数)\) 的时间找极小区间。

具体暴力会跳多少步呢？至少随机数据下是 \(O(n)\) 的，我想不出最坏情况的构造。

代码

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double dou;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mapa make_pair
typedef long double ld;
typedef unsigned long long ull;
#define ep emplace_back
template <typename T>inline void read(T &x){
	x=0;char c=getchar();bool f=0;
	for(;c<'0'||c>'9';c=getchar()) f|=(c=='-');
	for(;c>='0'&&c<='9';c=getchar())
	x=(x<<1)+(x<<3)+(c^48);
	x=(f?-x:x);
}
const int N=1e6+5;
int n;
int a[N];
int lp[N], rp[N];
mt19937_64 rnd(time(0));
ull hs[N], pre[N];
unordered_map<ull, int> h;
int f[N], g[N];
int mx[N][20], mn[N][20], lg[N];
inline int gmx(int l, int r){
	int t=lg[r-l+1];
	return max(mx[l][t], mx[r-(1<<t)+1][t]); 
}
inline int gmn(int l, int r){
	int t=lg[r-l+1];
	return min(mn[l][t], mn[r-(1<<t)+1][t]); 
}
inline int gmx(int l, int r, int x){
	return max(gmx(l, x-1), gmx(x+1, r));
}
inline int gmn(int l, int r, int x){
	return min(gmn(l, x-1), gmn(x+1, r));
}
int lpos[N], rpos[N];
int main(){
	// freopen("D:\\nya\\acm\\A\\test.in","r",stdin);
	// freopen("D:\\nya\\acm\\A\\test.out","w",stdout);
	read(n);
	for(int i=1; i<=n; ++i) hs[i]=rnd();
	for(int i=0; i<=2*n+1; ++i) f[i]=g[i]=1;
	h[0]=0;
	for(int i=1; i<=n*2; ++i) {
		read(a[i]);
		pre[i]=pre[i-1]^hs[a[i]];
		if(h.find(pre[i])!=h.end()) f[i]=1+f[h[pre[i]]];
		h[pre[i]]=i;
		if(lp[a[i]]==0) lp[a[i]]=i;
		else rp[a[i]]=i;
	}
	h.clear();
	h[pre[2*n]]=2*n+1;
	for(int i=n*2; i>=1; --i){
		if(h.find(pre[i-1])!=h.end()) g[i]=1+g[h[pre[i-1]]];
		h[pre[i-1]]=i;
	}
	h.clear();
	for(int i=1; i<=n*2; ++i){
		if(h.find(pre[i])==h.end()){
			lpos[i]=i-1;
			h[pre[i]]=i-1;
		}
		else lpos[i]=h[pre[i]];
	} 
	h.clear();
	for(int i=n*2; i>=1; --i){
		if(h.find(pre[i])==h.end()){
			rpos[i]=i+1;
			h[pre[i]]=i+1;
		}
		else rpos[i]=h[pre[i]];
	} 
	for(int i=2; i<=n*2; ++i) lg[i]=lg[i>>1]+1;
	for(int i=1; i<=n*2; ++i) mx[i][0]=rp[a[i]], mn[i][0]=lp[a[i]];
	for(int i=1; i<=lg[n*2]; ++i){
		for(int j=1; j+(1<<i)-1<=n*2; ++j){
			mx[j][i]=max(mx[j][i-1], mx[j+(1<<(i-1))][i-1]);
			mn[j][i]=min(mn[j][i-1], mn[j+(1<<(i-1))][i-1]);
		}
	}
	for(int i=1; i<=n*2; ++i){
		ll ans=(ll)f[i-1]*g[i+1];
		int l=lpos[i], r=rpos[i], lstr=i, lstl=i;
		while(true){
			if(l<=0||r>=2*n+1) break;
			if(l<=lp[a[i]]&&rp[a[i]]<=r) break;
			while(l>gmn(l, r, i)||r<gmx(l, r, i)) {
				if(l>gmn(l, r, i)) l=gmn(l, r, i);
				if(r<gmx(l, r, i)) r=gmx(l, r, i);
				if(l<=lp[a[i]]&&rp[a[i]]<=r) break;
			}
			if(l<=lp[a[i]]&&rp[a[i]]<=r) break;
			if(pre[r]==pre[lstr]||pre[l]==pre[lstl]){
				l=lpos[l]; r=rpos[r]; continue;
			} 
			lstr=r;
			ans+=(ll)f[l-1]*g[r+1];
			l=lpos[l]; r=rpos[r];
		}
		printf("%lld ", ans);
	}
	return 0;
}

posted @ 2025-10-10 20:04 Displace 阅读(18) 评论(0) 收藏举报

刷新页面返回顶部

Displace

vp + 补题 + 随机做题 记录一

The 2024 ICPC Asia East Continent Online Contest (II) D Query on Tree

0.刚看到题

1.怎么修改

2.怎么查询

3. \(b\) 怎么维护

4.需要干什么

1.预处理

2.DS维护

5.减少细节讨论

6.代码实现

The 3rd Universal Cup. Stage 7: Warsaw C Price Combo

0.刚看到题

1.转化下形式

2.怎么转移

The 3rd Universal Cup. Stage 10: West Lake F Triangle

0.刚看到题

1.确定 \(a_j+a_k>a_i\) 的数量

2.确定 \(a_k+a_j>a_i\) 的数量

The 3rd Universal Cup. Stage 10: West Lake B Generated String

0.刚看到题

1.只有一个区间怎么做

2.怎么拓展到原题

The 3rd Universal Cup. Stage 10: West Lake J Sheriruth

0.刚看到题

1.团

2.基环树

3.处理图

The 2nd Universal Cup. Stage 9: Qinhuangdao I Phony

0.刚看到题

1.细想

2.实现细节

3.bonus

The 2nd Universal Cup. Stage 9: Qinhuangdao C Palindrome

0.刚看到题

1.PAM

The 2nd Universal Cup. Stage 9: Qinhuangdao H Quake and Rebuild

0.刚看到题

1.怎么求 lca

2.怎么维护 \(nxt\)

3.怎么求 dfs 序

4.怎么求深度

5.卡常？

6.再分治！

The 3rd Universal Cup. Stage 12: Qinhuangdao K Diversity and Variance

0.刚看到题

1.怎么比较字典序。

2.怎么处理重复的 \(a_i\)

3.细节

The 3rd Universal Cup. Stage 13: Sendai G Count Pseudo-Palindromes

0.刚看到题

1.先构造点极端情况

2.如果能求极小合法区间

3.怎么求极小合法区间

公告

vp + 补题 + 随机做题记录一