组合数学学习笔记-第一章
1.1到1.7没有太难理解的,简单写写1.8个人题解。
3
可以扩展到 \(n\times m\) 的地图。
对地图进行黑白染色,坐标为 \((x,y)\) 的格子染成 \((x+y)\and 1\),这样可以保证每次行动会走到与当前颜色不同的格,因为经过了所有房间,所以经历了 \(n\times m-1\) 颜色变化。
当 \(n\times m\) 为奇数,即 \(n,m\) 均为奇数时,相当于颜色没变,而且 \((1,1)\) 与 \((n,m)\) 颜色相同,所以可能存在哈密顿路。
当 \(n\times m\) 为偶数,即 \(n,m\) 至少一个为偶数时,颜色发生变化。
当 \(n,m\) 都为偶数时,\((1,1)\) 与 \((n,m)\) 颜色相同,矛盾,一定不存在哈密顿路。
当 \(n,m\) 一奇一偶时,\((1,1)\) 与 \((n,m)\) 颜色不同,可能存在哈密顿路。
考虑能否构造,实际上是简单的,如果 \(n\) 为偶数交换 \(n,m\),然后按下面策略行动:
在奇数行,向右走到尽头,然后向下到下一行;在偶数行,向左走到尽头,向下到下一行。
综上,当 \(n,m\) 中至少有一个为奇数时图中存在哈密顿路。
4
(a)
简单DP,转移方程为 \(f_i=f_{i-1}+f_{i-2}\),斐波那契递推式。
(b)
可以状压DP一下,设 \(f_{i,s}\) 表示现在填到了第 \(i\) 列,第 \(i\) 列状态为 \(s\) 的方案数,\(s\) 的第 \(t(t=0,1,2)\) 位为0/1表示这位为空/满。
填新的一列时注意只能用横的骨牌覆盖上一列为空的位置。
\(g_{i}=f_{i, 7}\)
f[1][1+2]=f[1][1+4]=f[1][2+4]=f[1][0]=1;
for(int i=2; i<=6; ++i){
f[i][0]+=f[i-1][1+2+4];
f[i][1]+=f[i-1][2+4];
f[i][2]+=f[i-1][1+4];
f[i][4]+=f[i-1][1+2];
f[i][1+2]+=f[i-1][1+2+4]+f[i-1][4];
f[i][2+4]+=f[i-1][1+2+4]+f[i-1][1];
f[i][1+4]+=f[i-1][2];
f[i][1+2+4]+=f[i-1][0]+f[i-1][1+2]+f[i-1][2+4];
}
1到6的结果为:
0,3,0,11,0,41
把偶数项oeis一下,递推式为 \(f_{i}=4f_{i-1}-f_{i-2}\)。
考虑一下组合意义,我们不难手玩出 \(n=0\) 和 \(n=2\) 的答案为 1 和 3。现在考虑递推出 \(h_{n}=g_{2in}\)
从 \(i=n-1\) 来,新增两列有 \(n=2\) 的三种情况,所以有 \(3h_{i-1}\rightarrow h_{i}\)。
再往前考虑,对 \(i=n-2\),需要考虑新增四列,同时还不能与 \(i=n-1\) 时的转移重复,所以要求我们这新增的四列不能被拆分为分别新增两列,不难手玩出只有两种构造。
大概长这样:
所以有 \(2h_{i-2}\rightarrow h_{i}\)。
继续往前,同样我们需要构造出中间不可分割的骨牌连接方式,可以证明只有下面两种:

那么就有递推式:
用 \(h_{i}-h_{i-1}\) 即可得到 \(h_{i}-h_{i-1}=3h_{i-1}-h_{i-2}\),就是oeis上的递推式了。
6
对格子黑白染色,坐标为 \((x,y,z)\) 的格子染色为 \((x+y+z)\and 1\)。
一个骨牌覆盖一黑一白,偶数时黑格与白格数相等,奇数时黑格(1)比白格(0)多1。
奇数时中心坐标为 \((\frac{n+1}{2}, \frac{n+1}{2}, \frac{n+1}{2})\),如果 \(\frac{n+1}{2}\) 为偶数,那么中心是白格,否则是黑格。
所以有可能有解当且仅当 \(\frac{n+1}{2}\) 为奇数,即 \(n=4k+1\),\(k\) 为自然数。
7
必要性显然。
充分性:
把 \(a\times b\) 的骨牌拆成 \(a\) 个 \(1\times b\) 的骨牌,按照本章1.1的做法将棋盘按照图1-3赋值,并按照图1-4划分。
能进行 \(a\times b\) 的骨牌完美覆盖的棋盘显然也能进行 \(1\times b\) 的骨牌完美覆盖。
已经证明了如果有 \(1\times b\) 的骨牌的完美覆盖,需要 \(b\) 是 \(n\) 或 \(m\) 的约数。
所以我们最终的限制至少有 \(b\) 是 \(n\) 或 \(m\) 的约数。
对于 \(a\times b\) 的骨牌,相当于要覆盖 1 到 \(b\) 的数字每种各 \(a\) 个。
假设 \(b\) 是 \(m\) 的约数(否则交换 \(n,m\)),令 \(n=pb+t,m=qb\) 对于图1-4中上面的块,每种数字的数量是 \(p\times m\) 个;下面的块,每种数字的数量是 \(q\times t\)。
因为 \(a\) 是 \(b\) 的约数,所以 \(a\) 也是 \(m\) 的约数,所以上面的块满足每种数字的数量都是 \(a\) 的倍数,存在完美覆盖的方案。
对下面的块,已经不足以用 \(b\times a\) 的方式放置,所以就需要 \(a\) 是 \(t\) 的约数。
又因为 \(a\) 是 \(b\) 的约数,所以 \(a\) 是 \(n\) 的约数。
综上,命题充分条件为 \(a\) 为 \(n\) 和 \(m\) 的约数,\(b\) 为 \(n\) 或 \(m\) 的约数。
8
按照7中划分方式好像就显然了……
9
\(5\times 6\) 的棋盘能用 \(2\times 3\) 的骨牌完美覆盖,但不存在 \(2\times 3\) 的平凡完美覆盖。
13&17
证明 \(4k\) 阶的构造:
原矩阵元素满足:\(a_{i,j}=(i-1)*m+j\)。
考虑翻转后:
对于某一行,翻转操作相当于用 \(n^2+1\) 减去这个数,先不考虑加上 \(n^2+1\),相邻四个数翻转后和为0。所以一行的和为 \(2k(n^2+1)\),即 \(\frac{n(n^2+1)}{2}\)。
对于某一列,相邻四个数同理翻转后和为0,一列的和为 \(2k(n^2+1)\),即 \(\frac{n(n^2+1)}{2}\)。
对于对角线,可以发现翻转后对角线上元素没变,初始时可以计算得到和为 \(\frac{n(n^2+1)}{2}\),翻转后元素不变和也不变。
(奇数阶和 \(4k+2\) 阶不会证,会证了补上。)
14
打出来所有的和为15的三元组:
1 5 9
1 6 8
2 4 9
2 5 8
2 6 7
3 4 8
3 5 7
4 5 6
然后打出来每个数能参与构成几个三元组:
2 3 2 3 4 3 2 3 2
因为中间的数涉及到4个三元组,所以只能选5。
推证大概可以用暴力验证……
15
限制相当于 \(2+x+3+y=34,2+4+z+w=34\),即 \(x+y=29,z+w=28\)。
和等于29的有 13+16,14+15,和等于28的有 12+16,13+15。
只能分别选 14+15和 12+16
分类讨论一下,只有两种有可能合法:
2 15 3 14
4
16
12
2 14 3 15
4
16
12
对第一种,对角线上需要 1+7
如果填成
2 15 3 14
4 1
16 7
12
那么第二行需要和为 29 的,显然不能填出合法的。
如果填成
2 15 3 14
4 7
16 1
12
第二行需要和为 23 的,枚举一些也不能填出合法的。
对
2 14 3 15
4
16
12
分类讨论也能得出不合法的结果。
综上讨论,该矩阵不能填充为幻方。
19
(咕)
20
必要性:存在三染色方案。
充分性:图中有三角形,显然不能二染色。
跑了一下答案是 12
考虑一下组合解法,先确定10的颜色,那么12346789各自有两种染色方案。
对1而言,2和4与它颜色不同,2和3颜色不同,所以1和3颜色相同。
同理,可以归纳出1379颜色相同,2468颜色相同。
5只需要与2468颜色不同即可。
所以答案是 \(3\times 2\times 2=12\)
21
(a)
又是要求 \(x+y=x+z,y\neq z\),显然不行。
(b)
22
1 2 3 4 4 2 1 3
2 1 4 3 3 1 2 4
3 4 1 2 2 4 3 1
1 2 3 4 1 3 4 2
25
与1.1最后的证明类似,得到水平和竖直方向上都至少有10个垂直于这个轴的骨牌,那么一共就有至少20个骨牌,与18个骨牌矛盾。
26
31
第0位不平衡。
32
假设非平衡位除了第 \(j\) 位组成的二进制数为 \(x\),一定有 \(x<2^{j}\)。
假设这堆石头含有的非平衡位除了第 \(j\) 位组成的二进制数是 \(y\),那么只需要把这堆石头取到剩 \(x-y\) 个即可。
因为这堆石头含有第 \(j\) 位,所以是一定能取到只剩 \(x-y\) 个的。
33
局面1:全1堆,堆数为偶先手赢,为奇先手败。
局面2:全1堆+一堆>1,那么先手把这堆取成0/1转化为全1堆,先手必胜。
现在讨论一般的局面,先手的目标是把局面转化为局面2。
如果局面是非平衡态,那么先手可以用这样的策略:保证在出现局面2之前给后手留下非平衡态。
有这样的情况无法达到局面2:到先手时只剩下一堆且>1,此时先手直接取完,这样的局面是先手赢。
所以局面是非平衡态时,先手必胜。
如果局面是平衡态,那么给后手的一定是平衡态,所以先手必败。
综上,如果出现局面1则按堆数奇偶性讨论,堆数为偶先手必胜;
否则做nim博弈,若nim博弈先手必胜,则此博弈先手必胜。
34
后手必胜,保证自己放入的硬币数与先手上一次放入硬币数加起来为5即可。
35
先手必胜,先手第一回合随便放,之后用34的策略即可。
36
不知道和骨牌覆盖有啥关系,但是这不是我们 \(7!!=105\) 吗?
考虑每次选没被选的最小的新建一组,然后比它大的随便选一个和它一组。
37
1 3 2
3 2 1
2 1 3
1 x y z
x 2
y 3
z 4
开始分讨:
当x=3时,z=2,进一步填成:
1 3 4 2
3 2
4 3
2 4
可以明显看到第二行和第二列不能再填4了。
当x=4时,y=2:
1 4 2 3
4 2
2 3
3 4
同理第二行和第二列不能填3.
所以4阶的幂等对称拉丁方不存在。
38
考虑归纳:
1 . 两个点的情况显然成立。
2 . 假设 \(n=2k\) 时总能构造出来不相交的方案,现在考虑新增两个点:
如果这两个点的连线没有与之前连出的线相交,那么现在就是一个合法的方案;
如果和之前连出的线相交了 \(t\) 条,那么把这 \(t\) 条线全部拿出来。
按照交点横坐标对这 \(t\) 条线段排序,现在考虑交点横坐标最小的那条。
有这样两类情况和对应的修改方案:
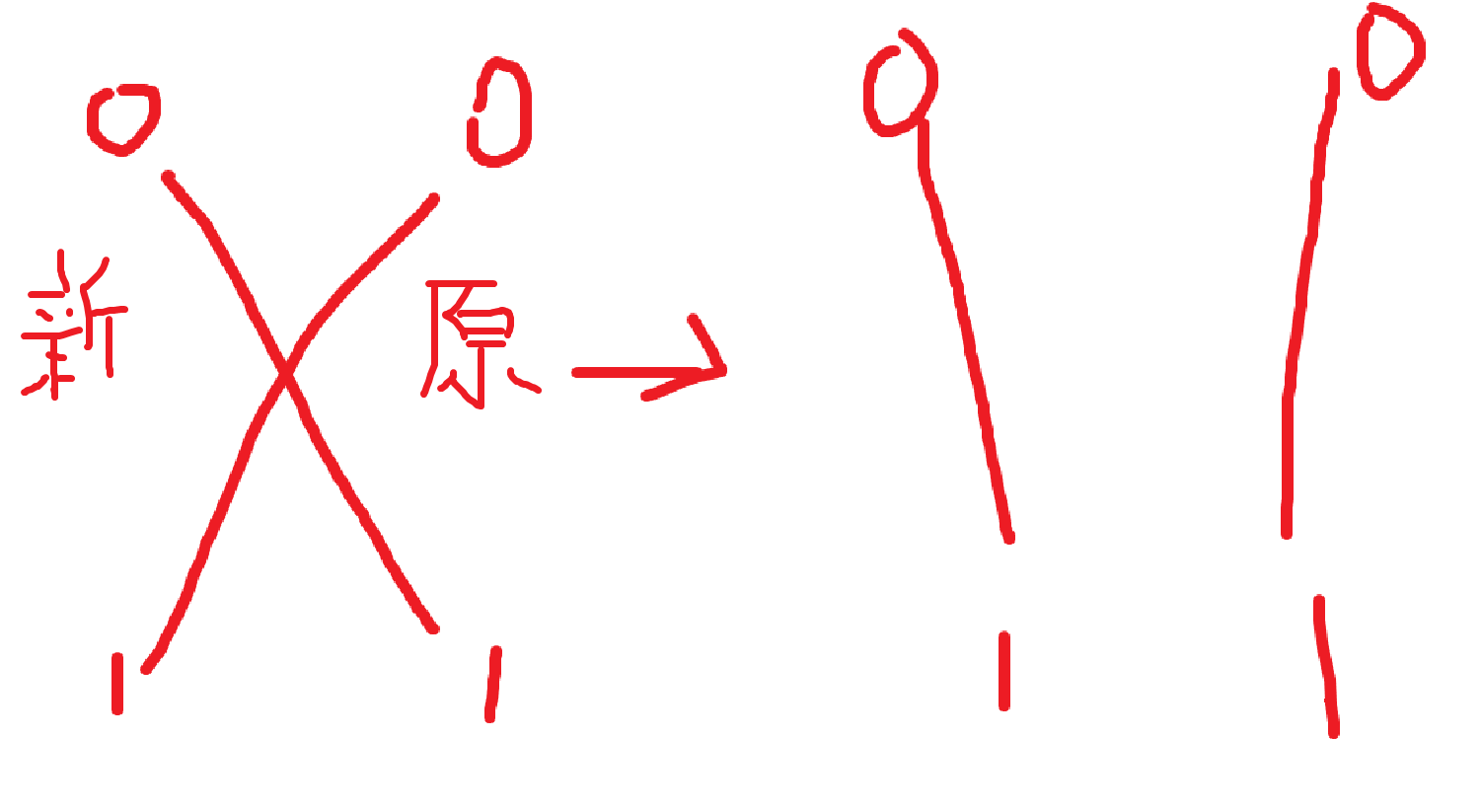
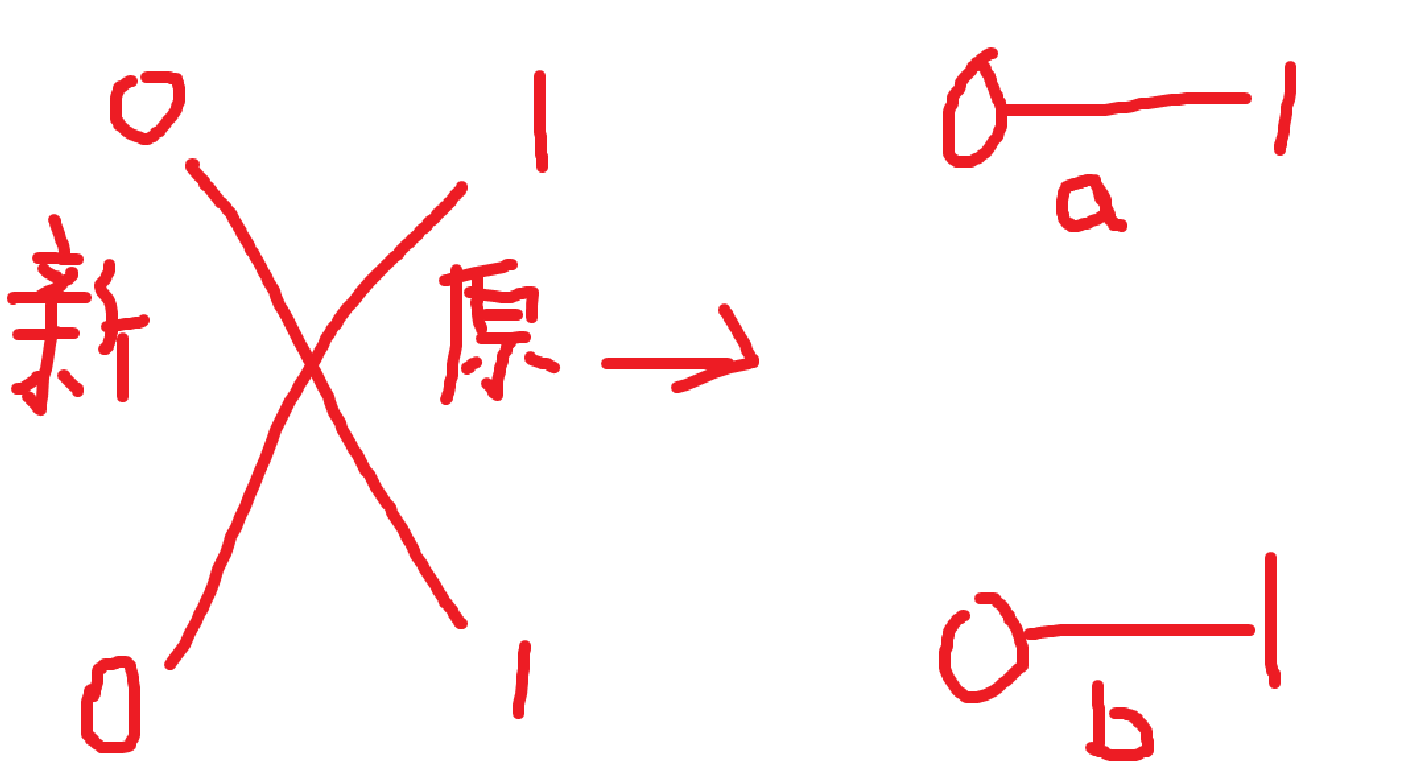
两种情况修改后显然相交的线段数变为最多 \(t-1\) 条。
这样调整下去,最终不会再有相交的线段。
所以在 \(n=2(k+1)\) 时也总能构造出不相交的方案。
综上,归纳成立。
39
\(n\times n\)
充分性:将两个L形骨牌相反方向可以合并出 \(2\times 4\) 的骨牌,显然 \(4|n\) 时可以被这样的骨牌完美覆盖,那么也就能被L形骨牌完美覆盖。
必要性:
若 \(n\) 为奇数,那么格子数不是4的倍数,显然不能被L形骨牌完美覆盖。
若 \(n\) 为 \(4k\),在充分性证明中已经讨论过完美覆盖的方案。
若 \(n\) 为 \(4k+2\),此时需要 \((2k+1)^2\) 个L形骨牌,这是个奇数。
把棋盘列间隔黑白染色,奇数列为白,偶数列为黑。
那么一个L形骨牌占据三白一黑或三黑一白。
棋盘上黑和白数量相同,L形骨牌选前者白比黑多2,后者白比黑少2,所以需要L形骨牌前者和后者数量相等。
又因为此时L形骨牌数量为奇数,所以不存在这样的方案。
综上,\(n\times n\) 的棋盘存在L形骨牌完美覆盖当且仅当 \(4|n\)。
\(n\times m\)
存在完美覆盖至少需要格子总数是 4 的倍数,所以 \(n,m\) 都为奇数显然不行。
当 \(n\) 为奇数,\(m\) 为偶数时,\(m\) 至少是4的倍数。
令 \(m=4k\),那么一共需要 \(nk\) 块骨牌,看做是 \(m\) 列的棋牌,对列做上一问的染色,那么黑=白,就需要 \(nk\) 是偶数。
因为 \(n\) 是奇数,所以 \(k\) 是偶数,即 \(m\) 是8的倍数。
我手玩了个 \(3\times 8\) 的,任意的都能以此为基础扩展。
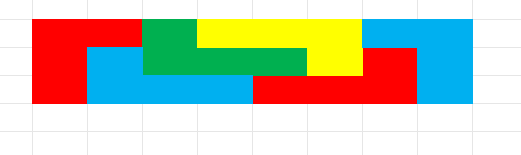
当 \(n,m\) 同时为偶数时,二者之积肯定是4的倍数。
设 \(n=2p,m=2q\),那么骨牌总数为 \(p,q\),还是对列染色,还是需要 \(pq\) 满足是2的倍数。
综上,有完美覆盖的充分必要条件为 \(nm\) 是8的倍数
42
给棋盘黑白染色。
当 \(n=2k\) 时,黑格与白格数量差为 \(k\),没有完美覆盖。
当 \(n=2k+1\) 时,黑格与白格数量差为 \(k+1\),没有完美覆盖。
所以楼梯式棋盘没有完美覆盖。
43
跑个爆搜,答案下界是6。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号