Math模板
Math
质数
【试除法判定质数】
-
质数和合数是针对所有大于1的 “自然数” 来定义的
-
所有小于等于1的整数既不是质数也不是合数.
bool is_prime(int x){ if(x<2)return false; for(int i=2;i<n/i;i++){ if(n%i==0)return false; } return true; } // n/i防止越界,相对于i*i<sqrt(n);
【分解质因数】
算术基本定理
void divide(int x){ for(int i=2;i<=x/i;i++){ if(x%i==0){ int s=0; while(x%i==0)x/=i,s++; cout<<i<<' '<<s<<endl; } } if(x>1)cout<<x<<' '<<1<endl; }
//先输出p再输出指数
【筛质数】
调和级数:当n趋近于正无穷的时候,1/2+1/3+1/4+1/5+…+1/n=lnn+c.(c是欧阳常数,约等于0.577左右.).
1.朴素筛
void get_primes(int n){ for(int i=2;i<=n;i++){ if(st[i])continue; primes[cnt++]=i; for(int j=i+i;j<=n;j+=i){ st[j]=true; } } }
2.线性筛
void get_primes(int n){ for(int i=2;i<=n;i++){ if(!st[i])primes[cnt++]=i; for(int j=0;primes[j]<=n/i;j++){ st[primes[j]*i]=true; if(i%primes[j]==0)break; } } }
约数
【试除法求约数】
vector<int>v; void solve(int x){ v.clear(); for(int i=1;i<=x/i;i++){ if(x%i==0){ v.push_back(i); if(i!=x/i) v.push_back(x/i); } } sort(v.begin(),v.end()); for(int i=0;i<v.size();i++)cout<<v[i]<<' '; cout<<endl; }
【约数个数】
给n个x,求乘积的约数个数或之和
//自己验算一下上式子正确性 void solve(int x){ unordered_map<int,int> prime; for(int i=2;i<=x/i;i++){ while(x%i==0){ x/=i; prime[i]++; } } if(x>1)prime[x]++; LL ans=1; for(unordered_map<int,int> ::iterator i=prime.begin();i!=prime.end();i++){ ans=ans*((*i).second+1)%mod; } }
【约数之和】
void solve(int x){ map<int,int> prime; for(int i=2;i<=x/i;i++){ while(x%i==0){ x/=i; prime[i]++; } } if(x>1)prime[x]++; long long ans=1; for(map<int,int>::iterator i=prime.begin();i!=prime.end();i++){ long long a=(*i).first,b=(*i).second; long long t=1; while(b--)t=(t*a+1)%mod; ans=ans*t%mod; } cout<<ans<<endl; }

【欧几里得算法】
gcd(a,b) = gcd(b,a mod b)
int gcd(int a,int b){ return b?gcd(b,a%b):a; }
欧拉函数
【欧拉函数】
互质是指最大公约数是1
//容斥原理证明欧拉函数 //1到n互质的个数即为(总个数-每个约数的倍数的个数,这些肯定不互质,一些会多,所以再加回来) //奇减偶加 int phi(int x){ int res = x; for (int i = 2; i <= x / i; i ++ ) if (x % i == 0){ res = res / i * (i - 1); while (x % i == 0) x /= i; } if (x > 1) res = res / x * (x - 1); return res; }
【筛法求欧拉函数】
LL solve(){ phi[1]=1; for(int i=2;i<=n;i++){ if(!st[i])prime[cnt++]=i,phi[i]=i-1; for(int j=0;prime[j]<=n/i;j++){ st[prime[j]*i]=true; if(i%prime[j]==0){ phi[prime[j]*i]=phi[i]*prime[j]; break; } phi[prime[j]*i]=phi[i]*(prime[j]-1); } } }
欧拉定理:如果a与n互质,则有a的phi[n]次方模n等于1
当n为质数时(a为任意自然数),phi[n]=n-1;则a的n-1次方模n等于1(费马定理)
快速幂
【快速幂】
//快速求出a的k次方mod P 的结果 //预处理a的2的1次方到2的logk次方的结果 //把k拆成若干个2的次幂之和 LL qmi(int a,int k,int p){ LL res=1; while(k){ if(k&1){ //看 k的个位,是1的话,让res*a的2的几次幂 res=(LL)res*a%p; } k>>=1; //接着走 a=(LL)a*a%p; //a方 } return res%p; }
【快速幂求逆元】
三大余数定理:
加法:(a+b)%c=a%c+b%c
减法:(a-b)%c=a%c-b%c
乘法:(ab)%c=(a%c)(b%c)
乘法逆元的定义
a存在模p的乘法逆元的充要条件是gcd(a,p) = 1
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(mod m),则称 x 为 b 的模 m 乘法逆元,记为 b的-1次方(mod m)。 b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,b的(m−2)次方 即为 b 的乘法逆元。
//求其a的p-2次方即为其乘法逆元 if(a%p==0)puts("impossible"); else cout<<qmi(a,p-2,p)<<endl;
扩展欧几里得算法
裴蜀定理: 对任何[整数a、b和它们的最大公约数d,关于未知数x和y的线性丢番图方程(称为裴蜀等式):
ax + by = m 有解当且仅当m是d的倍数,d其实就是最小可以写成ax+by的正整数
【扩展欧几里得算法】
int exgcd(int a,int b,int &x,int &y){ if(!b){ x=1,y=0; return a; } int d=exgcd(b,a%b,y,x); y-=a/b*x; return d; }
【线性同余方程】
ai×xi≡bi(modmi)
中国剩余定理
高斯消元
【高斯消元解线性方程组】
int gauss(){ int r,c; for(c=0,r=0;c<n;c++){ //枚举每一列 int t=r; for(int i=r;i<n;i++){ //从r行开始(上面的每一行第一个数都已成为一) if(fabs(a[i][c])>fabs(a[t][c])) t=i; //找到c这一列最大的数所对应的行,为了后续便又把它交换你上去 } if(fabs(a[t][c])<eps)continue; //是0的话就继续 for(int i=c;i<=n;i++)swap(a[t][i],a[r][i]); //将此行交换上去 for(int i=n;i>=c;i--)a[r][i]/=a[r][c]; //将这行第一个数变为1 for(int i=r+1;i<n;i++){ //将从r到n行对应的此列都变为0 if(fabs(a[i][c])>eps){ for(int j=n;j>=c;j--){ a[i][j]-=a[r][j]*a[i][c]; //a[i][c]倍 } } } r++; } if(r<n){ for(int i=r;i<n;i++){ if(fabs(a[i][n])>eps) return 2;//无解 一个数=0 } return 1; //无穷解0=0,此方程可以被别的方程表示 } for(int i=n-1;i>=0;i--) //求解 for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j]; return 0; }
组合数学
一、直接算
void init(){ for (int i = 0; i < N; i ++ ) for (int j = 0; j <= i; j ++ ) if (!j) c[i][j] = 1; else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; } //公式,dp
二、公式+逆元
fact[0]=1,infact[0]=1; for(int i=1;i<=N;i++){ fact[i]=(LL)fact[i-1]*i%mod; infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod; } cout<<fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;
三、Lucas定理

int C(int a,int b,int c){ if(b>a)return 0; int res=1; for(int i=1,j=a;i<=b;i++,j--){ res=(LL)res*j%p; res=(LL)res*qmi(i,p-2,p)%p; } return res; } int lucas(LL a,LL b,int p){ if(a<p&&b<p)return C(a,b,p); return (LL)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p; }
四、高精度算出结果
int primes[N], cnt; int sum[N]; bool st[N]; void get_primes(int n){ for (int i = 2; i <= n; i ++ ){ if (!st[i]) primes[cnt ++ ] = i; for (int j = 0; primes[j] <= n / i; j ++ ){ st[primes[j] * i] = true; if (i % primes[j] == 0) break; } } } int get(int n, int p){ int res = 0; while (n){ res += n / p; n /= p; } return res; } vector<int> mul(vector<int> a, int b){ vector<int> c; int t = 0; for (int i = 0; i < a.size(); i ++ ){ t += a[i] * b; c.push_back(t % 10); t /= 10; } while (t){ c.push_back(t % 10); t /= 10; } return c; } int main(){ int a, b; cin >> a >> b; get_primes(a); for (int i = 0; i < cnt; i ++ ){ int p = primes[i]; sum[i] = get(a, p) - get(a - b, p) - get(b, p); } vector<int> res; res.push_back(1); for (int i = 0; i < cnt; i ++ ) for (int j = 0; j < sum[i]; j ++ ) res = mul(res, primes[i]); for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]); puts(""); return 0; }
五、Catalan数

/*给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为 2n 的序 列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。*/ //画图,0往右走,1往上走,所有到达n,n点的合法(即0的个数比1多方案数就是总的减去终点经过上一条线对称的点的方案数
容斥原理
二项式定理
容斥原理
for(int i=0;i<m;i++)cin>>p[i]; for(int i=1;i<1<<m;i++){ //2的m次方,1表示选此数 int cnt=0,t=1; //cnt统计1个数,奇加偶减 for(int j=0;j<m;j++){ //t统计选的这些数相乘 if(i>>j&1){ if((LL)t*p[j]>n){ t=-1; break; } t*=p[j]; cnt++; } } if(t!=-1){ if(cnt%2){ res+=n/t; } else res-=n/t; } } cout<<res<<endl;
博弈论
Nim游戏
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
n堆石子亦或为1时,先手必胜,否则必败
while(n--){ int x; cin>>x; res^=x; } if(res)puts("Yes"); else puts("No");

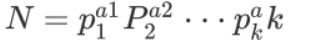


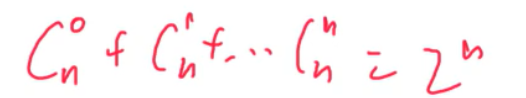

 浙公网安备 33010602011771号
浙公网安备 33010602011771号