「BUAA OO」Unit1
一、作业分析
1. 第一次作业
第一次接触OO作业面对大段的表达式定义时,关于应该如何化简,自己其实并没有非常清晰的思路,甚至可以说是不知从何下手。在这样的情况下,我最终决定采用了课程组提供的官方包,选择使用预解析模式完成作业。
思路:
由题目,我们可以很容易地发现,输入的表达式经过解析后的形式为f1 op xxxx, f2 op xxxx,f3 op xxxx......fn op xxxx,故我们只需要将按此顺序进行运算,将化简后得到的fn输出即可。我在Main中创建了一个命名为expF的ArrayList来保存最新的fi(1<=i<=n),并建立了Parser类对读入的String进行解析,将解析出的op和运算项(v1、v2)传入Lexer;Lexer类对v1、v2进行判断,将其传入Exp或Term进行进一步解析,再根据op进行运算得到result。将计算得到的result保留在fi内。
类图:

框架非常丑非常尴尬,我自己也看不下去了。
代码复杂度分析
由于方法较多,在此仅列出红色的条目。


注:
- ev(G)是基本复杂度,衡量非结构化程度,ev(G)高意味着难以模块化和维护。
- iv(G)是模块设计复杂度,衡量模块之间的调用关系,iv(G)高意味着模块之间的耦合性高,难以隔离和复用。
- v(G)是圈复杂度,衡量结构的复杂程度,v(G)是说明代码难以测试和维护。
- CogC是认知复杂度,衡量代码的难以理解的程度,CogC高说明代码比较难以理解。
其中,Parser类的parser方法由于自己的规划十分杂乱,CogC极高,达到了46。Exp的sub和add方法也由于非结构化的设计,使得模块较难维护,ev(G)较高。
2. 第二次作业
相信大家也能感觉到,我的第一次作业完美地诠释了什么叫“面向过程”编程。没有对象,没有架构,只有想完成作业的满满求生欲。
于是,在第二次作业,yaj同学的漫漫重构之路开始了......
思路:
考虑了程序的层次性与可拓展性,我在第二次作业采用了递归下降法处理表达式的解析。通过利用形式化表述定义,我将表达式分成了三个层次:因子(f(x, y ,z)、sum、三角函数、变量x、数字)、项(乘除)、表达式(加减),这三种结构对应了三种对象。下面分别进行讨论对这些对象的解析:
- 对于表达式的解析:表达式由项和加减符号组成,可以模仿上面对“项”的解析方法对步骤进行拆分:
- 表达式的开头可以直接调用项的解析方法,若第一次解析出+/-号,则作为参数传入parserTerm()方法。
- 解析完一个项,同样有两种可能:如果下一个字符是加减符号,那么读入这个符号并做处理,然后下一个符号一定是一个项。
否则,说明表达式的解析结束了。
- 对于项的解析:项由因子和乘除符号组成,因此解析项分为下面几个部分:
- 项的开头一定是一个因子,因此我们可以直接调用因子的解析方法,将任务交给“因子”类;若第一次解析出+/-号,则与传入的参数op进行整合后,将整合后的符号作为参数传入parserFactor()方法。
- 因子后面跟着的字符有两种可能:乘除或其他符号。如果下一个字符是乘除符号,那么读入这个符号并做处理。此时跟在乘除号后面的一定还是一个项,回到第一步。
否则,说明这个项的解析已经结束了,后面的字符不再是这个项的内容(不可能是数字,否则会在前面一步解析),退出并返回构造好的项即可。
- 对于因子的解析:
- 若判断下一个字符为"(",则跳过此字符,然后再次调用parserExpr方法,返回解析后的表达式后,跳过字符")";
- 否则,若判断下一个部分为函数f/g/h,则将函数替换为对应表达式(细节:先替换x)后,再次使用parserExpr()方法对其进行化简;
- 否则,若判断下一个部分为sum求和函数,则将函数替换为对应表达式。类似上一条的处理方法;
- 否则,若判断下一个部分为三角函数sin、cos,将其部分传入对应类进行解析化简后返回;
- 否则,若判断下一个字符为x,则继续解析是否为幂函数,将其套入Variable类进行解析(注:若指数为1,则返回值为1的Number类);
- 否则,下一个部分必为数字,进行数字的读取。
若传入的符号为"-",使用一次Neg()方法。对因子的解析结束。
存储表达式的树状结构示意图:
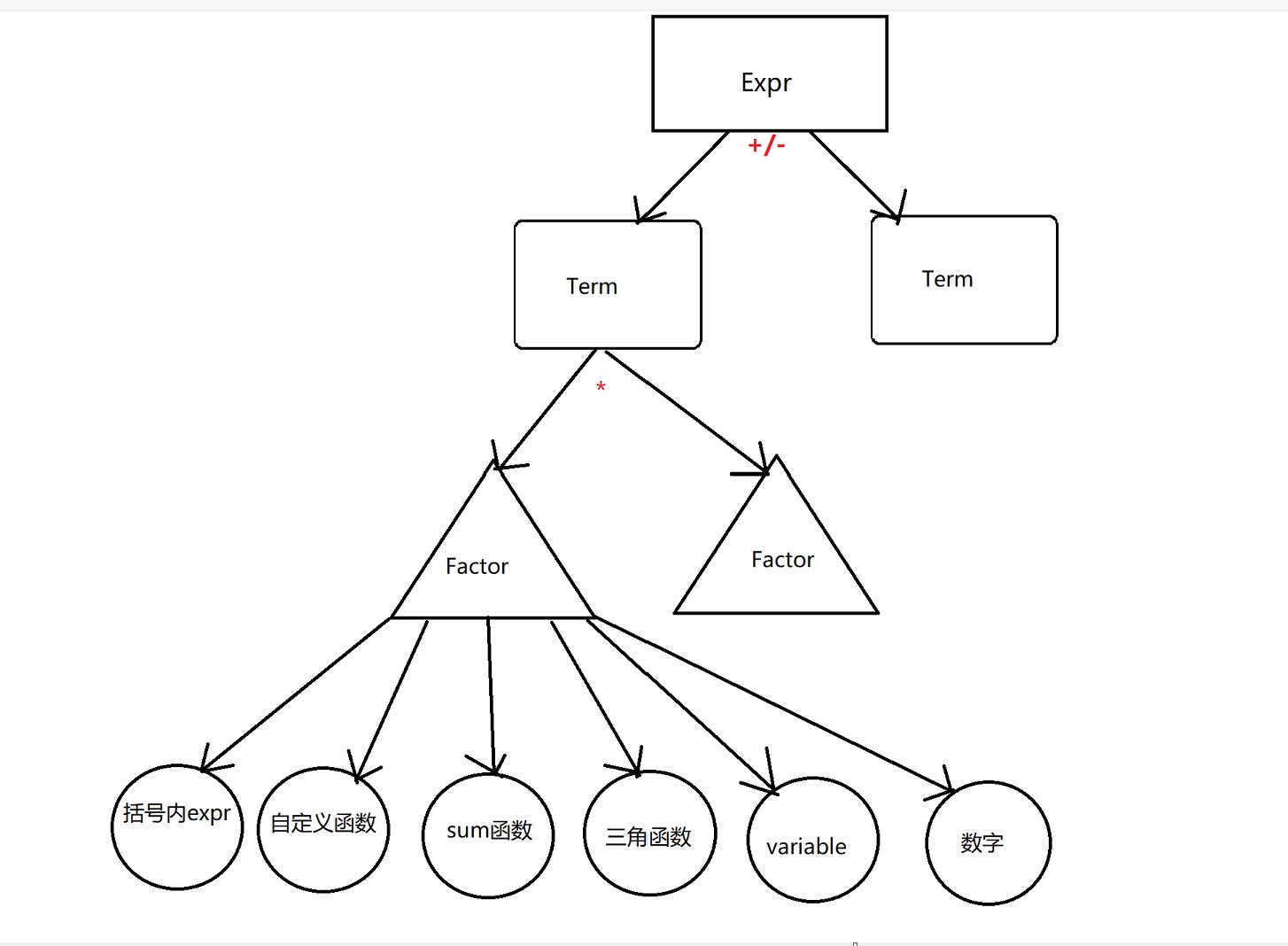
类结构设计与图:
- 表达式的解析
-
- Parser:对Lexer进行从Expr到Term再到Factor的递归下降解析。
Lexer:储存着输入的字符串,pos从0开始逐步解析。

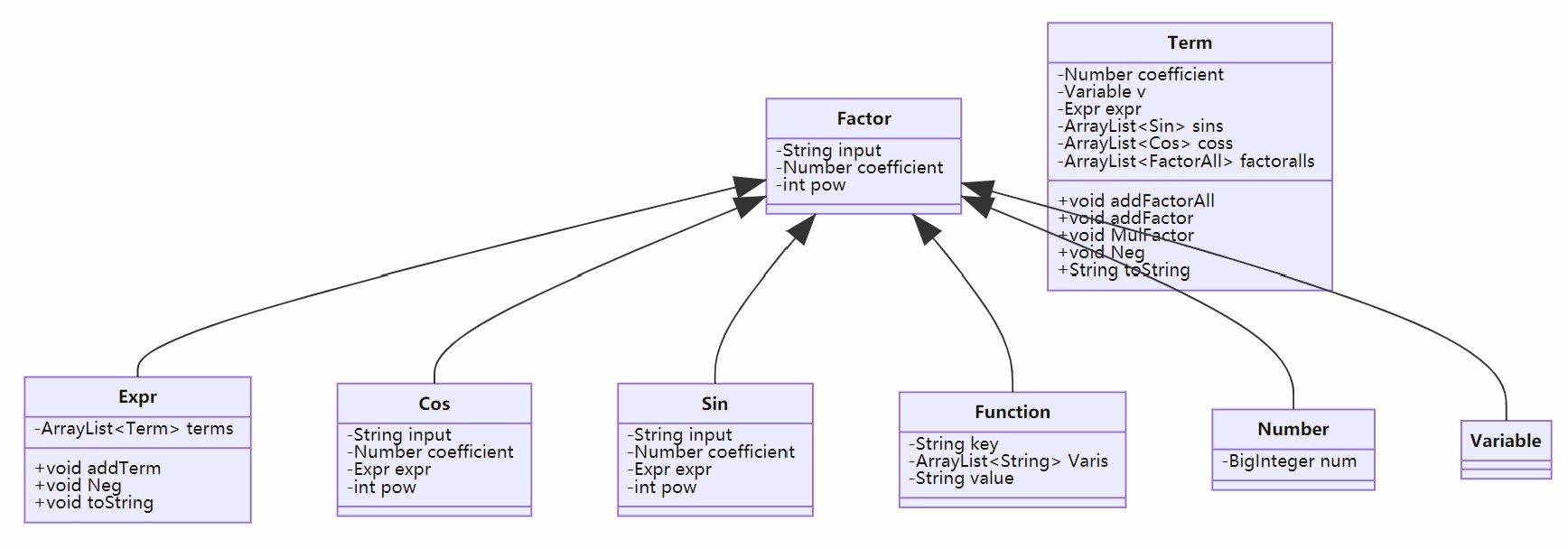
2. 表达式的存储
-
Expression:"表达式",为一个或若干个 "项" 的组成。Term:"项",为数字、variable、expr、三角函数的组成。Factor:“因子”,对应表达式树的叶子节点:Number:数字常数,内部数据为一个BigInteger,支持加减/乘/幂/比较等运算。Variable:由变量 "x"和其指数组成。Sin:三角函数sin ,内部含有一个因子(Factor)和一个指数 。Cos:三角函数cos ,内部含有一个因子 (Factor)和一个指数。Expression:子表达式(对应"表达式因子"),内部含有一个表达式 (Expression)
这些类之间形成了一个有层次的树状结构
3. 表达式的运算
-
Add:进行加法运算。实例变量A、B分别为传入的表达式,输出result是进行加法后得到的结果expr(其中,细分为termAddterm、FactAddFact)。Sub:进行减法运算。实例变量A、B分别为传入的表达式,输出result是进行减法后得到的结果expr(其中,细分为termSubterm、FactSubFact)。Mul:进行乘法运算。实例变量A、B分别为传入的表达式,输出result是进行乘法后得到的结果expr(其中,细分为termMulterm、FactMulFact)。
代码复杂度分析
方法复杂度分析
同上,由于作业的类较多,方法数目也较多,所以 Method Metrics 生成的表格过长,无法在一屏内完整截图,故只展示总体情况与出现红色的条目。



总体来看,这次作业中整体的复杂程度和耦合程度还算正常,仅存在少数方法的指数超标。其中,parserFactor由于需要解析的因子的可能性比较多,含有较多的 if-else 分支,进行了较多的判断;MulFactor中由于需要进行因子的遍历,故ev(G)的值较高。
类复杂度
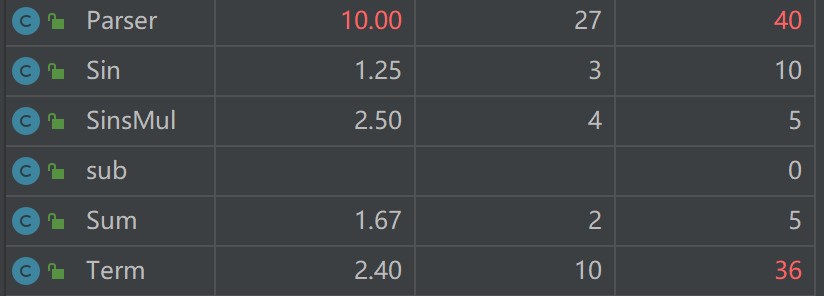

总体基本符合高内聚低耦合,但是表达式解析parser类和"项" ( Term ) 类的圈复杂度仍然较高,可以进一步简化。
3. 第三次作业
由于在第二次作业中采用了递归下降的处理方法,本身已经能够处理多层嵌套表达式和函数调用的括号展开与化简,第三次在原有基础上的拓展较为轻松。
第三次作业的内容与结构与第二次基本相同,但经过研讨课上同学的经验分享和小组讨论,我将原有的Factor内的实例变量合并改进为【a*x**b*sin()**c*cos()**d】的形式(a、b、c、d均为数字),处理时强化边解析边化简的思想,使其更加简洁易懂方便。
二、优缺点分析
优点
- 在表达式的存储上采用继承的方法
- 采用了递归下降法进行输入表达式的解析,使得程序具有良好的可拓展性
- 使用HashMap进行数据的管理
- 严格遵守"形式化表述",层次清晰且不易出错
缺点
- 某些类与类之间存在高度的代码重复,暂时没有找到解决的办法
- 某些类的性能处理不佳,使用了许多if-else
三、Bug分析
在debug的过程中,我先使用简单的单个因子进行测试,再逐渐地增加表达式的复杂度进行测试。由于自己对正则表达式并不是很熟悉,最初写完作业degug的时候,发现很多pattern的写法有错误,调试的时候花了很长的时间。在对自定义函数进行replace替换时,会出现如f(y, x),先将y替换为x,x再替换为x的情况,此时如果直接按原有顺序进行替换,会造成冲突。在请教同学后,我使用了无论何时都优先对x进行替换的方法,解决了此问题。
在对他人程序进行debug的过程中,由于我并不是很了解该如何写脚本进行测试,故更多地是自行构造数据进行测试。
四、心得体会
本单元的oo让我感受到自己还有很多需要提升的地方。在能力方面,对于JAVA语言的使用,我还并不是很熟悉,需要多加练习,去感受“面向对象”的思想;很多语法的用法和编程思想也需要我在课下花更多的时间去了解、去实践,才能写出更合理的架构,让自己的代码更具有良好的可拓展性。而在个人的习惯方面,我曾在第一次作业发布后,因不知从何下手而踌躇了几天,拖到最后实在没有想法才采用了官方包的预解析模式进行完成。在完成的过程中,自己才在一边敲打键盘的过程中,一边慢慢体会到了题目的用意,可最后只能感叹一句:“要知道这样我就早点开始了!” ——尽早地采取行动,是这几次作业带给我最大的经验教训。同时,如何平衡oo与其他课程之间的时间,对于我来说也是非常重要的一点。
希望在接下来的作业中,我能够继续加油,完成新的挑战~ 在此也非常感谢曾经给予我指点的助教和同学,你们的帮助对我非常非常重要。




