Tensorflow2.0-基础

数据载体

python：list，列表 numpy：ndarray tensorflow：tensor，多维数组
可使用不同数据类型，可嵌套
不连续存放，
动态指针数组 效率低，占空间大
由于高度灵活性，不适合做数值计算		 数据类型相同
每个元素占空间相同，连续存储
占空间小，读写速度快
占用的是内存，只能在cup运算		 可运行于gpu，tpu
支持多种计算环境
高速实现复杂算法

数据类型

  • tensorflow张量就是多维数组，不管是多少维的，都是张量

  • tensorflow数字默认类型：tf.int32,tf.float32,不同类型不能操作

  • numpy默认的小数是float64，

转换数据类型时：低-->高,防止数据溢出

整数转bool，0F，非零T

常用函数

  • a = tf.convert_to_tensor(numpy数据) # 将numpy数组转为tensor

  • tf.is_tensor(a) #检查是否是张量 

  • isinstance(a,tf.Tensor)
isinstance(a,numpy.ndarray)

特殊张量

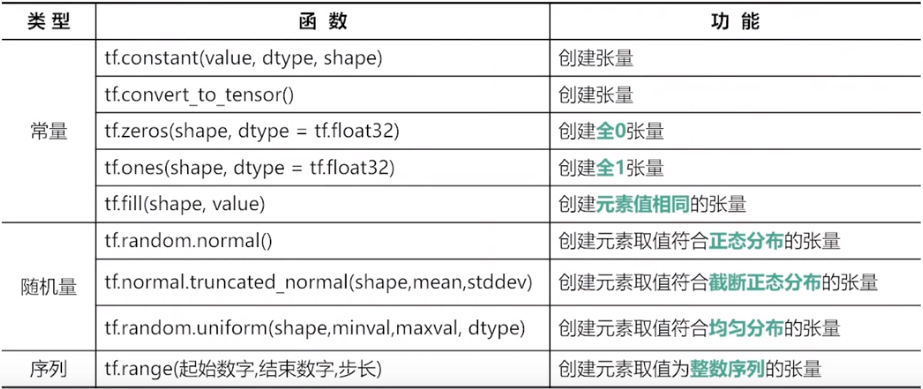
image-20200608121339812

tf.zeros(shape,dtype) # 全0张量，默认是float32
tf.ones()

tf.fill(shape,value) # 自动判断数据类型，填充相同数字
tf.constant(9,[2,3]) # 也可以

tf.random.normal(shape,mean,stddev,dtype) # 正态随机分布，默认均值为0，标准差为1，float32
tf.random.truncated_normal(shape,mean,stddev,dtype)
# 截断的正态分布，截断标准是2倍标准差，值不会偏离均值2倍标准差
tf.random.uniform(shape,min,max,,type) # 均匀分布，不包含最大，包括最小
tf.random.shuffle(x) # 沿着第一维打乱
tf.random.set_seed(8) # 设置随机种子，仅仅一次有效

tf.range(start,limit,delta,dtype)# 创建序列，前闭后开，默认从0开始，步长为1

张量属性

  • ndim：维度
  • dtype：类型
  • shape：形状
  • tf.shape(a):张量形式返回形状
  • tf.size(a):总数
  • tf.rank(a):维度

注意

  • 在cup中张量与numpy共享内存，只是使用不同方式读取使用它
  • 多维张量内存中是一位数组连续存储

改变形状

b = tf.reshape(tensor,shape)

轴也可以是负数，表示从后向前

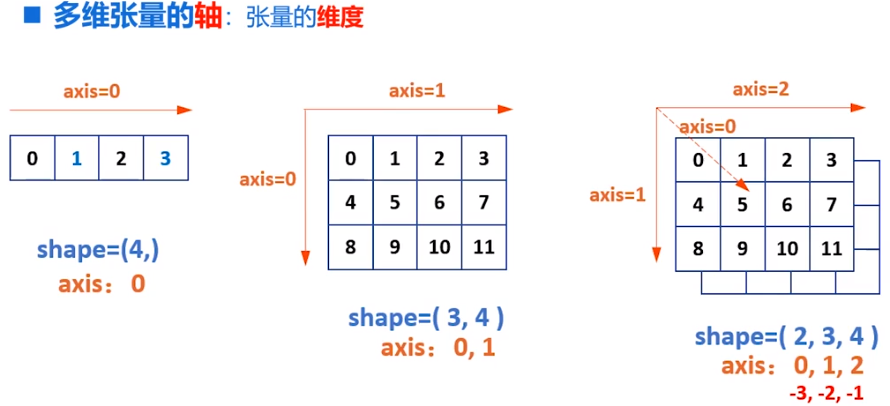
image-20200608123050283

tf.expand_dims(input,axis) # 增加维度，维度长度为1
a = tf.constant([1,2]) # shape(2,)
b = tf.expand_dims(a,1) # shape(2,1) 元素数不变形状变了而已
c = tf.expand_dims(a,0) # shape(1,2)

a = tf.range(24)
b = tf.reshape(a,[2,3,4])
b1 = tf.expand_dims(b,0) # shape(1.2,3,4)
b1 = tf.expand_dims(b,1) # shape(2,1,3,4)
b1 = tf.expand_dims(b,2) # shape(2,3,1,4)
b1 = tf.expand_dims(b,3) # shape(2,3,4,1)

# 删除维度 只能删除长度为1的维度,并不会改变数量，只是改变了存储
tf.squeeze(input,axis)

a = tf.range(24)
b = tf.reshape(a,[2,1,1,3,4])
tf.squeeze(t) #shape->(2,3,4)
tf.squeeze(t,[0,1]) # shape->(1,3,4)

#交换维度,改变了视图，也改变了存储顺序
tf.transpose(a,perm)  # 对于二维张量，默认是转置
# x.shape-->(2,3)
tf.transpose(x,[1,0]) # shape->(3,2)

# 拼接,不会增加维度
tf.concat(tensor,axis) #
# 分割张量
tf.split(value,num_or_size,axis=0)
# num_or_size:2 表示平均切位2个
# [1:2:1] ,按比例切割

# 只改变视图，存储顺序不变

# 堆叠与分解
tf.stack(values,axis) # 
a = tf.constant([1,2,3])
b = tf.constant([1,2,3])
tf.stack((x,y),axis=0) # shape(2,3)
tf.stack((x,y),axis=1) # shape(3,2)



tf.unstack(values,axis)
a = tf.constant([[1,2,3],[1,2,3]])
tf.stack(a,axis=0) # shape(3,) 2个
tf.stack(a,axis=1) # shape(2,) 3个

# 索引
# 与numpy几乎相同
# 一维:a[1],二维:a[1][1],a[1,1],三维:a[1][1][1],a[1,1,1]

# 切片[起始:结束:步长]，步长为负数表示反向切片
# 前闭后开，起始，结束，步长可省略
# 二维数据，与一维类似，逗号隔开

# 数据提取
tf.gather(params,indices)
a = tf.range(5)
tf.gather(a,[0,2,3]) # 从a中提取0,2,3下标的元素

a = tf.random.normal([4,5])
tf.gather(a,axis=0,[0,2,3]) # 去获取0 2 3行
tf.gather(a,axis=1,[0,2,3]) # 去获取0 2 3列
# 每次只有一个维度
# 多维获取
tf.gather_nd(b,[[0,0],[1,1],[2,3]]) # 指定每个元素坐标
tf.gather_nd(三维元素,[[0,0],[1,1],[2,3]]) # 指定每个元素坐标，此时采样的是三个点，每个点三个通道
tf.gather_nd(三维元素,[[0],[1],[2]]) # 类似获取三个面

深度学习

一元线性回归

  • 平均损失函数：\(Loss=\frac{1}{2}\mathop{\sum}\limits_{i=1}^{n}(y_i-\bar{y_i})^2=\frac{1}{2}\mathop{\sum}\limits_{i=1}^{n}(y_i-(wx_i+b))^2\)

  • 均方误差：\(Loss=\frac{1}{2n}\mathop{\sum}\limits_{i=1}^{n}(y_i-\bar{y_i})^2\)

    • \(\frac{1}{2}\)是为了求导方便，
    • 使用平方做误差，防止正负误差抵消
    • 此时Loss与误差单调性相同

基于均方误差最小化求解模型的方法：最小二乘法

w,b作为自变量，取何值时，Loss最小？，求极值问题：极值点偏导数为0

\(\frac{\partial Loss}{\partial w}=\mathop{\sum}\limits_{i=1}^{n}(y_i-b-w_i)(-x_i)=0\)

\(\frac{\partial Loss}{\partial b}=\mathop{\sum}\limits_{i=1}^{n}(y_i-b-w_i)(-1)=0\)

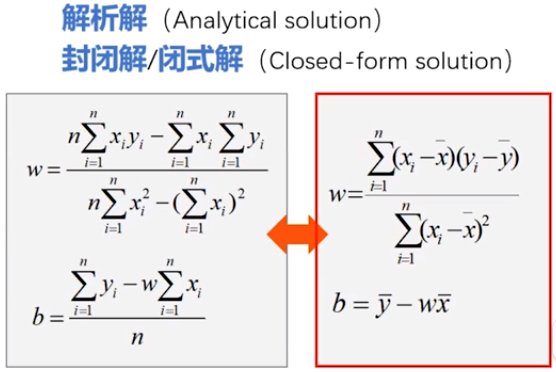
image-20200608142106038

梯度下降

  • 解析解：严格推导得出，任意精度满足方程
  • 数值解：近似计算得到，给定精度下满足方程

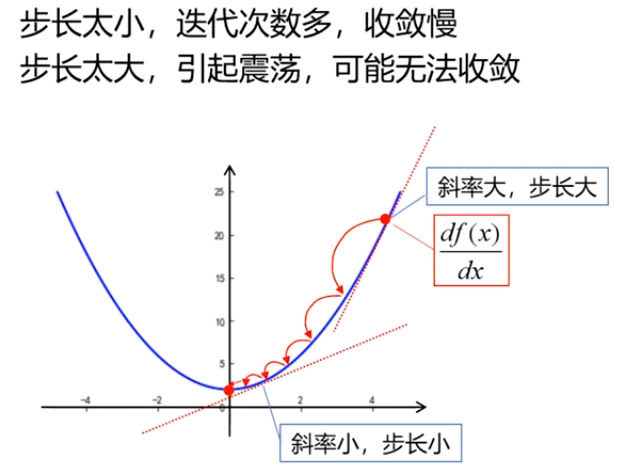
image-20200608143534763

\(步长=\eta \frac{df(x)}{dx},\eta:学习率\)

\(x^{(k+1)}=x^k-步长\)

  • 根据斜率实现自适应调整步长
  • 自动确定下一次方向
  • 保证收敛性

二元凸函数类似：

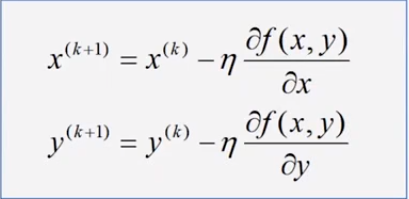
image-20200608144115993

梯度：\(\vec{gard}f(x,y)=\frac{\partial f(x,y)}{\partial x}\vec{i}+\frac{\partial f(x,y)}{\partial y}\vec{j}\)

只要损失函数是凸函数，就可以使用梯度下降法，最快速度更新w，得到极值点，

凹凸性定义国内外方式不同，很可能相反

image-20200608145907632

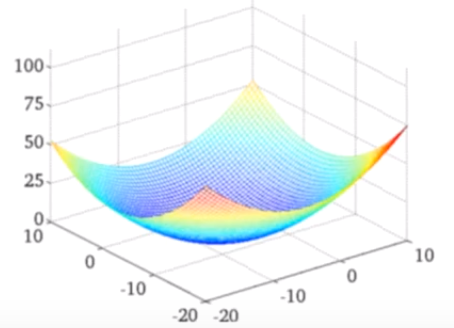
image-20200608145923365

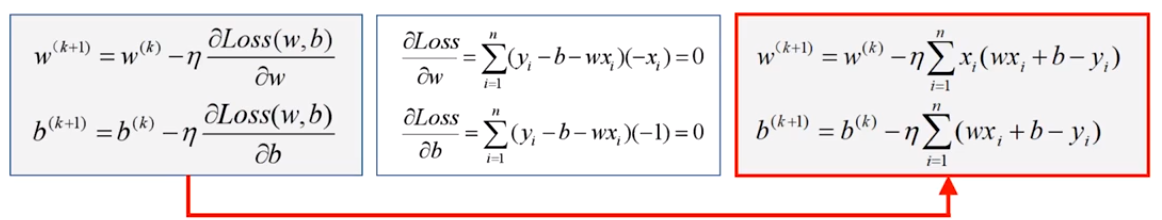
image-20200608150020916

image-20200608150238087

对于凸函数，只要学习率足够小，可以一定收敛，但极大会震荡，极小会很难收敛

超参数：开始先定义的

示例：

import numpy as np
import matplotlib.pyplot as plt
x = np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y = np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])

learning_rate=0.00001
iter=100
display_step=10

mse=[]
for i in range(0,iter+1):
    # 计算偏导数，根据导数公式带入数据即可
    dL_dw=np.mean(x*(w*x+b-y))
    dL_db=np.mean(w*x+b-y)
    
    w=w-learning_rate*dL_dw
    b=b-learning_rate*dL_db
    
    pred=w*x+b
    Loss=np.mean(np.square(y-pred))/2
    mse.append(Loss)
    if i %display_step==0:
        print("i:%i,Loss:%f,w:%f,b:%f"%(i,mse[i],w,b))
        
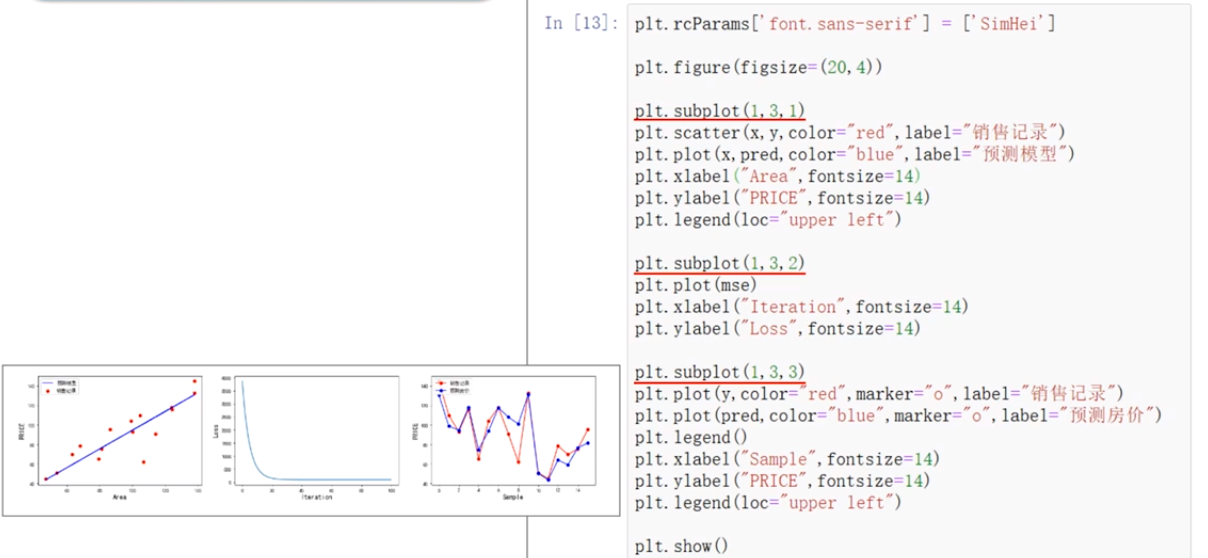
     plt.rcParams['font.sans-serif']=['SimHei']
plt.figure()
plt.scatter(x,y,color='red',label="销售记录")
plt.scatter(x,pred,color="blue",label="梯度下降法")
plt.plot(x,pred,color="blue")
plt.plot(x,0.89*x+5.41,color="red")

plt.xlabel("Area",fontsize=14)
plt.ylabel("Price",fontsize=14)
plt.legend(loc="upper left")
plt.show()

image-20200608154745250

多元例子

数据归一化/标准化：将数值限制在范围内，防止某个属性影响过大

线性归一化：\(x*=\frac{x-min}{max-min}\)等比例缩放[0,1]

标准归一化：\(x*=\frac{x-\mu}{\sigma}\),归一化均值为0，方差为1，

非线性归一化:对数，指数，正切

根据数据确定

dL_dw=np.matmul(np.transpose(X),np.matmul(X,W)-Y)
W=W-lrarning_rate*dL_dW
pred =np.matmul(X,W)

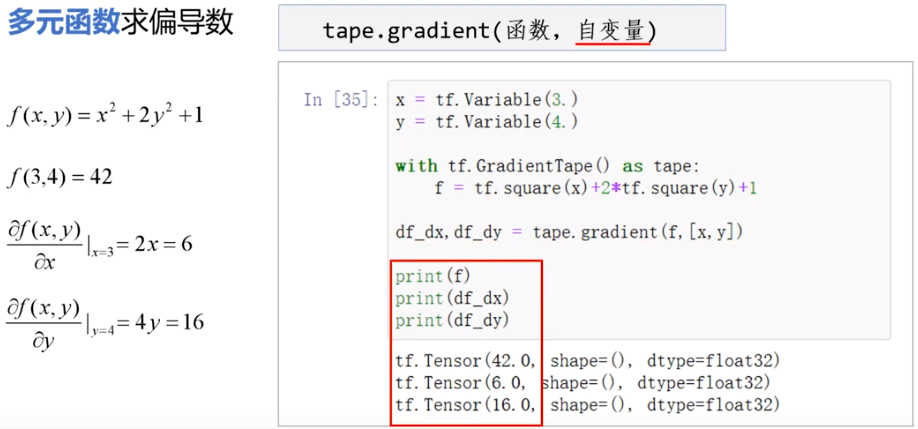
自动求导

tf.Variavle()可训练变量，可修改，有assign(),assgin_add()等，x.trainable属性等

tf.constant不同，是不可修改的

with GradienTape(persistent=True,watch_access_variables=Flase) as tape:
    tape.watch(x)
    y=tf.square(x)
grad=tape.gradient('函数','自变量') # 
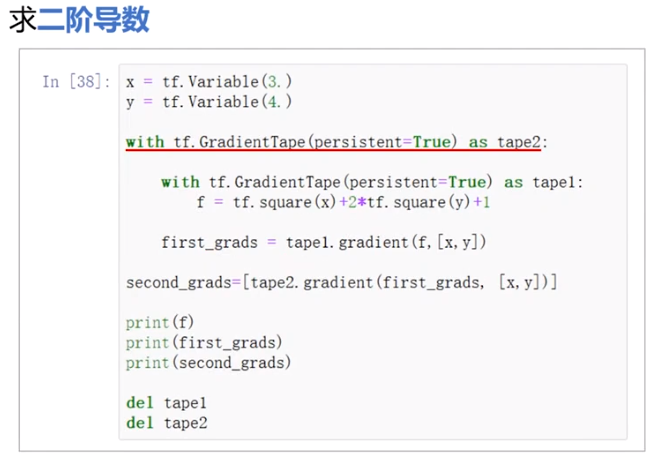
# persistent 为true可多次调用gradient
# 	为True时最后要 del tape
# watch默认为True，为False时需要手动watch变量

image-20200608174933672

image-20200608175043042

posted @ 2020-06-08 19:51  下雨天,真好  阅读(226)  评论(0)    收藏  举报