随笔2022-1-30

咱就是说闲不住了

话不多说先看题：

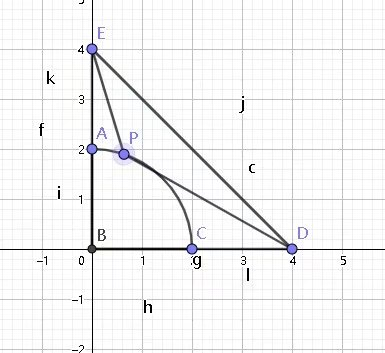
在等腰\(Rt△EBD\)中，A为EB中点，以B为圆心，BA长为半径作弧，交边BD于C点。现在弧AC上有一动点P，求 \((EP+PD)_{min}\)。

啊……咱就是在抖音上无聊刷到的，那个老登说这是什么“超难最值问题”，结果就这么个破题，大家可以试试看。

PS:顺便晒晒游戏战绩(一年前的纪录，挺菜的)

试完了吗

首先，有点几何直观的人都能猜到P在弧AC中点时，\(EP+PD\) 取得 \(min\) 值。但是怎么去证明呢？

法一：

看到这个，毫无疑问的想到“阿氏圆”问题。但是……传统的阿氏圆问题中，我们的 "\(k\)" 一般给定的值都等于 \(\frac{r}{BD}\) ，这时 \(k=1≠\frac{1}{2}\)。
那么，怎样改进传统的办法使它切合这个题目呢？
emm,有同学之前读过我的另一篇 Blog : 阿氏圆拓展，在该篇文章中，我们引入了椭圆来解决问题。同样的，如果在这题也引入椭圆，会不会好办呢？
于是，我们以 E、D 为焦点，构造椭圆，当椭圆与圆弧AC相切时，\(P\) 运动到切点（也就是AC中点）\(F\) 时，\(EP+PD\) 取得 \(min\) 值。

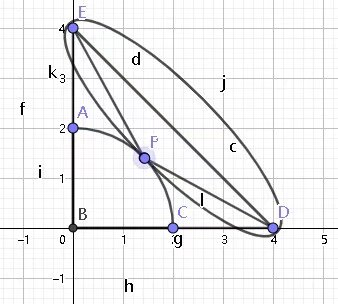
法二

遇事不决就暴力。我们设 \(P(x,\sqrt{4-x^2})\)(0<x<2) ，然后根据两点距离公式，可得 \(PE=\sqrt{x^2+(4-\sqrt{4-x^2})^2}\),\(PD=\sqrt{(\sqrt{4-x^2})^2+(4-x)^2}\),两者相加，整理得:\(PE+PD\)=\(2(\sqrt{5-2x}+\sqrt{5-2\sqrt{4-x^2}})\)。
那么这个式子怎么求最小值呢？
em,不妨令 \(y=\sqrt{4-x^2}\) ，函数 \(f(x,y,z)=\sqrt{5-2x}+\sqrt{5-2y}+z(x^2+y^2)\)。（很显然 \(x^2+y^2=4\)）
然后要求极值想到对原函数进行求导：
\(f'(x)=-\frac{1}{\sqrt{5-2x}}+2xz=0 \space\space\)①
\(f'(y)=-\frac{1}{\sqrt{5-2y}}+2yz=0 \space\space\)②
\(f'(z)=x^2+y^2-4=0\)
然后由 ① 得到 \(\frac{1}{2x\sqrt{5-2x}}=z\)，由 ② 得到 \(\frac{1}{2y\sqrt{5-2y}}=z\) ，所以 \(x\sqrt{5-2x}=y\sqrt{5-2y}\) ，考虑解根式方程，得到 \(x=y\) 或 \(x=\sqrt{5-2y} , y=\sqrt{5-2x}\) 。变形得：\(x^2-y^2=2(x-y)\) 即 \((x+y)(x-y)=2(x-y)\) ，显然此时 \(x-y≠0\) ，故 \(x+y=2\) 则 \((x+y)^2=4\) 又因 \(x^2+y^2=4=(x+y)^2-2xy\)，所以 \(xy=0\) ，又因 \(x,y>0\)，此情况舍去。
所以结果只能是 \(x=y\) ，联立 \(x^2+y^2=4\)，解得 \(x=y=\sqrt 2\)
唔，所以答案就是 \(P(\sqrt 2,\sqrt 2)\) 时取得最小值。

法三:

和法二思路差不多，从 \(PE+PD=2(\sqrt{5-2x}+\sqrt{5-2\sqrt{4-x^2}})\) 这里，我们令 \(y=\sqrt{4-x^2}\) 。显然的，根据 0<x<2 得到 0<y<2。 然后原式可以整理成 \(\sqrt{5-2x}+\sqrt{5-2y}\)，根据基本不等式，有 \(\sqrt{5-2x}+\sqrt{5-2y}≥2\sqrt[4]{25-10(x+y)+4xy}\)。又因为 \(x^2+y^2=4\) ,所以 原式≥\(2\sqrt[4]{25-10(x+y)+2[(x+y)^2-4]}=\sqrt[4]{2(x+y-\frac{5}{2})^2+\frac{9}{2}}\)。然后，因为 \(x^2+y^2=4,0<x<2,0<y<2\)，所以说 \(x+y≤\sqrt{2(x^2+y^2)}=2\sqrt2\),而 \(x+y\) 最小值 =2。故 \(\sqrt[4]{2(x+y-\frac{5}{2})^2+\frac{9}{2}}≥\sqrt[4]{33-20\sqrt2}=\sqrt[4]{25-20\sqrt2+8}=\sqrt[4]{(5-2\sqrt2)^2}=\sqrt{5-2\sqrt2}\)，所以说，原式 \(min\) 在 \(x=y\) 时取得，即 \(x=y=\sqrt2\)时，\((PE+PD)_{min}=2\sqrt{5-2\sqrt2}\)

法四：

这题其实就是经典的“古堡朝圣”问题。首先对于这类问题又一个普遍结论：当 \(BP\) 平分 \(∠EBD\) 时，原式取得 \(min\) 。这个应该是对于我们初中生最友好的解法了。证明过程如下：

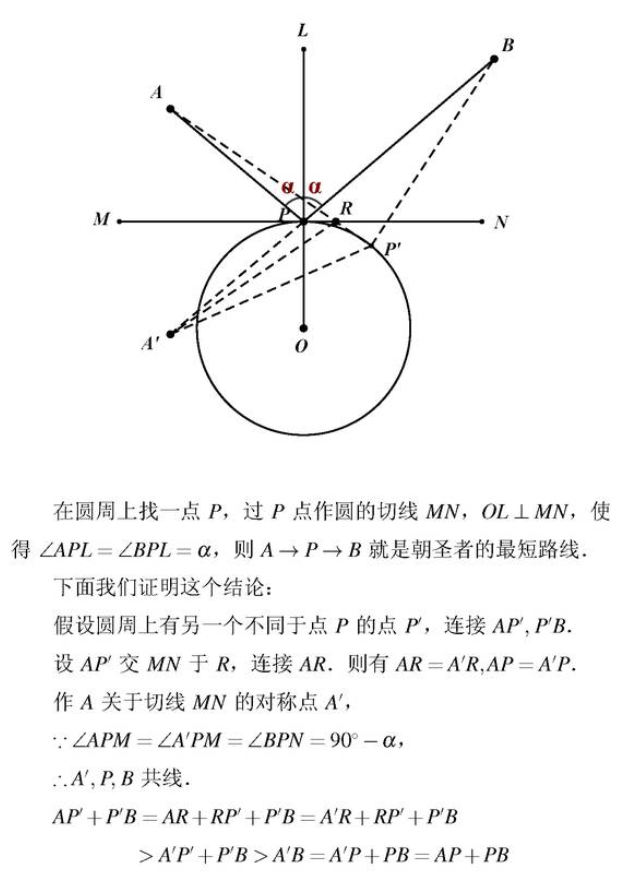
但是呢这个问题属于是特殊一点的，也就是说 \(OA=OB\) （模型中的）。这样的情况下我们可以通过尺规作图找到 \(P\) 点，但是一般的问题没有固定做法。

结束语

感谢 青D(也就是我自己啦)提供椭圆解法
感谢 超次元提供求导解法
感谢 TEoS提供基本不等式解法
感谢 百度提供古堡朝圣解法