算法回顾 之 动态规划

动态规划的核心是最优子结构原理(Optimal substructure), 最优子结构表示如下:
    设 问题( C, N={1,2,...,n}, {wi}i∈N, {vi}i∈N ) 的最优解是 (y1,y2,...,yn), 那么
    (y2,...,yn)是 问题( C-w1, N={2,...,n}, {wi}i∈N, {vi}i∈N ) 的最优解。

 

动态规划经典算法有:
1.  数字三角形问题
2.  最长公共子序列问题
3.  字符串的编辑距离    

… …

1. 数字三角形问题
        7
       3 8
      8 1 0
     2 7 4 4
    4 5 2 6 5
找出一条从顶点至底部的路径，使该路径经过的数字总和最大(每个数只能到达其左下或右下的相邻数字)
用二维数组a存放数字三角形

    7
    3 8
    8 1 0
    2 7 4 4
    4 5 2 6 5

int[][] b=new int[a.length][a[0].length];
//...
b[0][0]=a[0][0];
for(int i=1;i<a.length;i++){
    for(int j=0;j<a[0].length;j++){
        if(j==0){
            b[i][j]=a[i][j]+b[i-1][j];
        }
        else{
            b[i][j]=(a[i][j]+b[i-1][j-1]) > (a[i][j]+b[i-1][j]) ? (a[i][j]+b[i-1][j-1]) : (a[i][j]+b[i-1][j]);
        }
    }
}
//...

遍历b数组的最底层, 最大值即最大路径长度。

 

2. 最长公共子序列问题
例如: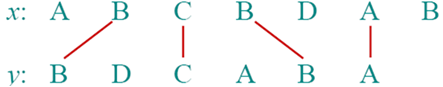
 
又如:
序列一 1,2,3,4,5,6,7,8,9,10,11
序列二 1,7,8,9,2,3,5,6,4,11,10
两序列的最长公共子序列为:1,2,3,5,6,11或1,2,3,5,6,10, 长度为6

解: 设c[x,y,i,j]表示 数组x从x[0]~x[i] 与 数组y从y[0]~y[j] 的最长公共子序列的长度, 那么, 有:
c[x,y,i,j]=0                                                 if   i<0 || j<0
c[x,y,i,j]=c[x,y,i-1,j-1]+1                              if   i>=0, j>=0, x[i]==y[j]
c[x,y,i,j]=max{ c[x,y,i-1,j] , c[x,y,i,j-1] }         if   i>=0, j>=0, x[i]!=y[j]

代码如下：

public static int trying(int[] A, int[] B, int i, int j){
    if(i<0||j<0){
        return 0;
    }
    else if(A[i]==B[j]){
        return trying(A,B,i-1,j-1)+1;
    }
    else{
        return Math.max(trying(A,B,i-1,j),trying(A,B,i,j-1));
    }
}

 

3. 字符串的编辑距离
将字符串A变换为字符串B所用的最少删除、插入、替换操作数称为字符串A到B的编辑距离, 记为d(A, B) , 设两个字符串为A[1:m]和B[1:n],
设D[i, j]=d(A[1:i], B[1:j])。
单字符a, b的编辑距离为:
d(a, b)=0    if a==b
d(a, b)=1    if a!=b
那么, D[i, j]可以递归地定义为: D[i, j]=min{ D[i-1,j-1]+d(A[i], B[j]) , D[i-1, j]+1 , D[i, j-1]+1 }
代码如下：

public static int isEqual(char a, char b){
    if(a==b)
        return 0;
    else
        return 1;
}

public static int Min(int a, int b, int c){
    int min=Math.min(a,b);
    return Math.min(min,c);
}

//A[0:i]与B[0:j]的编辑距离
public static int findDistance(int i, int j){
    if(i==0 && j==0){
        return isEqual(A.charAt(i), B.charAt(j));
    }
    else if(i!=0 && j!=0){
        return Min(findDistance(i-1,j)+1, findDistance(i,j-1)+1, findDistance(i-1,j-1)+isEqual(A.charAt(i), B.charAt(j)));
    }
    else{
        if(i==0){
            if(isEqual(A.charAt(i), B.charAt(j))==0)
                return j;
            else
                return findDistance(i,j-1)+1;
        }
        else{
            if(isEqual(A.charAt(i), B.charAt(j))==0)
                return i;
            else
                return findDistance(i-1,j)+1;
        }
    }
}