算法回顾 之 递归

这张图是一个递归的例子, 很有中国特色。

递归经典算法:
1.  Hanoi问题
2.  八皇后问题
3.  归并排序
     … …

1. Hanoi问题:

/**
 * @(#)Hanoi.java
 * @ 汉诺塔问题
 *
 * @author Chen.
 * @version 1.00 2011/6/10
 */

public class Hanoi {
    public Hanoi() {
    }

    //将最上面的盘从X柱移到Y柱
    public void move(char X,char Y){
        System.out.println(X+"----->"+Y);
    }

    //将上面的n个盘从X柱通过Y柱移到Z柱
    public void hanoi(int n,char X,char Y,char Z){
        if(n==1)
            move(X,Z);
        else if(n>1){
            hanoi(n-1,X,Z,Y);
            move(X,Z);
            hanoi(n-1,Y,X,Z);
        }
    }

    public static void main(String[] args) {
        Hanoi h=new Hanoi();
        h.hanoi(3,'A','B','C');
    }
}

2. 八皇后问题: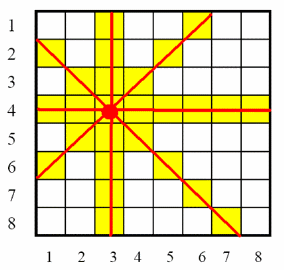

//在1~j-1列已确定的情况下, 确定第j列到第8列的所有情况
public void trying(int j){
    for(int i=1;i<=8;i++){
        if(a[i]==0&&b[i-j+7]==0&&c[i+j-2]==0){
            x[j]=i;//x[j]等于i:表示第j列的“后”, 在第i行上
              a[i]=1;
            b[i-j+7]=1;
            c[i+j-2]=1;
            if(j<8)
                trying(j+1);
              else{
                //打印x[1]~x[8]
            }
            a[i]=0;
            b[i-j+7]=0;
            c[i+j-2]=0;
        }
    }
}

其中, 数组a、数组b、数组c 分别表示对应 行、主对角线、副对角线 是否在“皇后”的杀伤范围内, 1表示在, 0表示不在, 下图表示数组b, 即主对角线的情况, b[i-j+7]对应下图的斜线。
           1    2     3     4     5     6     7     8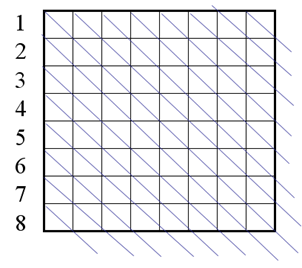

3. 归并排序

//对a[i]~a[j]进行排序
public void sort(int[] a, int i, int j){
    if(i<j){
        sort(a,i,(i+j)/2);
        sort(a,((i+j)/2)+1,j);
        merge(a,i,(i+j)/2,j);
    }
}

//将a[i]~a[m](有序)  与  a[m+1]~a[j](有序) 进行合并, 并输出每次合并的结果
public void merge(int[] a, int i, int m, int j){
    if(i>=j) return;
    int x=i;
    int y=m+1;
    int length=j-i+1;
    int[] b=new int[length];
    int k=0;
    while(x<=m && y<=j){
        if(a[x]<a[y]){
            b[k++]=a[x++];
        }
        else if(a[x]==a[y]){
            b[k++]=a[x++];
            b[k++]=a[y++];
        }
        else{
            b[k++]=a[y++];
        }
    }

    if(x>m)
        while(y<=j)
            b[k++]=a[y++];
    else
        while(x<=m)
            b[k++]=a[x++];
    for(int u=0;u<length;u++){
        a[u+i]=b[u];
        System.out.print(b[u]+" ");
    }
    System.out.println();
}

总结:
应用递归解决问题应满足3个条件：

1. 问题可以定义、转化为同类的新问题,但与原问题所处理的对象有所不同,它们在有规律地递增或递减。

2. 可以通过转化使问题解决（化为递归）

3. 要有明确的递归结束条件（递归结束）