Suffix Array：后缀数组学习笔记

后缀排序

后缀排序，顾名思义就是给后缀排个序。朴素做法是 $O(n^2\log n)$ 的，无法接受。因此诞生了基于倍增思想的后缀排序算法。

其中倍增思想在集训队论文中讲得很好，在此不再赘述。这里主要讲代码实现。

const int N=2e6+10;
char s[N];
int n,m,sa[N],rk[N],tp[N],b[N];
void Rsort(){
	for(int i=1;i<=m;i++)b[i]=0;
	for(int i=1;i<=n;i++)b[rk[i]]++;
	for(int i=2;i<=m;i++)b[i]+=b[i-1];
	for(int i=n;i>=1;i--)sa[b[rk[tp[i]]]--]=tp[i];
}
void get_SA(){
	m=127;
	for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
	Rsort();
	for(int k=1,p=0;k<=n&&p<n;k<<=1){
		p=0;
		for(int i=n-k+1;i<=n;i++)tp[++p]=i;
		for(int i=1;i<=n;i++)if(sa[i]>k)tp[++p]=sa[i]-k;
		Rsort();
		for(int i=1;i<=n;i++)tp[i]=rk[i];
		rk[sa[1]]=1,p=1;
		for(int i=2;i<=n;i++){
			if(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+k]==tp[sa[i]+k])rk[sa[i]]=p;
			else rk[sa[i]]=++p;
		}
		m=p;
	}
}

我们来分析每部分代码的作用。

for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
Rsort();

这两行是把 $s[i]$ 作为第一关键字，把 $i$ 作为第二关键字，进行排序，求出初始的 $sa[i]$ 。

接下来，$k$ 表示当前步长为 $k$ 的已经处理完了，要处理 $2k$ 的。所以实际上倍增到 $k$ 的时候，$k$ 在上一阶段已经处理完了（一开始循环部分外对 $k=1$ 的排序也能印证这一点）。

for(int i=n-k+1;i<=n;i++)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>k)tp[++p]=sa[i]-k;

这两行是在更新 $tp$ 数组。回顾一下 $tp[i]$ 的定义：第二关键字排名为 $i$ 的字符串的起始位置。所以当前我们需要求出，步长为 $2k$ 时，第二关键字排名为 $i$ 的字符串的起始位置。

对于 $\forall i\in[n-k+1,n]$，以 $i$ 为起点的，长度为 $k$ 的子串都没有第二关键字了（第二关键字显然超出 $n$ 了，不存在），那么就将这些没有第二关键字的串的第二关键字排名放到最前面（相对顺序不重要，因为这些字串的长度不同，第一关键字肯定不同，第二关键字不会影响最终排名）。

对于一般情况，我们可以用已经求出的，步长为 $k$ 的 $sa[i]$ 更新 $tp$ 数组。具体地，从小到大枚举 $sa[i]$，这样保证了 $tp$ 也是有序的。如果 $sa[i]>k$，意味着 $sa[i]-k$ 这个位置是存在的，把这个位置装进 $tp$ 里。

接下来看 Rsort 函数，这部分是关键。

void Rsort(){
	for(int i=1;i<=m;i++)b[i]=0;
	for(int i=1;i<=n;i++)b[rk[i]]++;
	for(int i=2;i<=m;i++)b[i]+=b[i-1];
	for(int i=n;i>=1;i--)sa[b[rk[tp[i]]]--]=tp[i];
}

首先，m 是名次的个数，也就是桶的值域。我们把 $k$ 步长的每个名次出现的次数进行统计，然后做一遍前缀和。

接下去，从发明者的角度理解吧。我们要排序每个位置开始的，长度为 $2k$ 的字符串。那么对于第 $i$ 个字符开始的，我们需要知道它的前半段和后半段在步长 $k$ 意义下的排名。前半段的排名很显然是当前的 $rk[i]$。假设以 $i$ 为起点的字符串的第二关键字的排名是 $j$，即 $tp[j]=i$ ，那么第二关键字就是 $j$（请注意 $tp$ 数组我们在上面就处理好了）。

更进一步的，我们可以用一个二元组表示：

\[(rk[i],j)_i \]

其中，$tp[j]=i$。

那么我们换一种方式表示，就是：

\[(rk_{tp_i},i)_{tp_i} \]

接下来，我们要对这些二元组进行排序，设计算法的时候，因为 $sa_i$ 的定义是排名第 $i$ 的位置，又因为 $tp_i$ 就是位置了，所以考虑 $sa[?]=tp_i$。

考虑这个 $?$ 是多少。看代码，桶 $b$ 中存的是第一关键字，所以桶的同一个位置的第一关键字相同，我们只需要比较第二关键字即可，也就是说，这是 LSD（Least Significant Digit first）基数排序。这也是为什么要先更新 $tp$ 的原因。

思考到这，“为什么要求前缀和”这个问题就呼之欲出了。答案就是为了求当前第一关键字下的排名。从大到小枚举 $i$，那么当前 $tp_i$ 位置对应的 $rk[tp_i]$ 对应的，做过一遍前缀和的桶，就是当前 $?$ 的值。即 sa[b[rk[tp[i]]]--]=tp[i]; 。为什么要 -- 呢？因为统计完后，对应的桶位置少了 $1$。因为从大到小枚举，所以相同第一关键字时，更后被枚举到的，排名更小。

for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=1,p=1;
for(int i=2;i<=n;i++){
	if(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+k]==tp[sa[i]+k])rk[sa[i]]=p;
	else rk[sa[i]]=++p;
}
m=p;

这段是在更新 $rk$ 数组，上面已经更新完 $tp$ 和 $sa$ 了。$tp$ 是为更新 $sa$ 服务的，因此 $tp$ 在这里已经没用了，可以用未被更新的 $rk$ 覆盖它。至于为什么需要用到旧的 $rk$ 在下面会解释。

在倍增过程中，会存在两段字串相等的情况。判断两个字串相等的部分是 if(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+k]==tp[sa[i]+k])rk[sa[i]]=p; ，这么做的原因是很显然的，画个图就很清晰了。在这里我们用到了 $tp$ ，也就是旧的 $rk$ 数组，这就是上面为什么要保留旧 $rk$ 的原因。

最后 m=p 是什么意思呢？$p$ 是当前阶段的 $rk$ 个数，也就是下一阶段的第一关键字个数，就是下一阶段 Rsort 时的桶大小。所以把 m 赋为 p 。

$height$ 数组

定义

$height[1]=0$

$height[i]=lcp(suf(sa[i-1]),suf(sa[i]))$

引理一

$height[rk[i]]\ge height[rk[i-1]]-1$，即 $height[rk[i]]>height[rk[i-1]]$

证明见此处。

引理揭示了一个重要的道理：$lcp(sa[rk[i]],sa[rk[i]-1])$ 至少为 $height[rk[i-1]]-1$，那么我们按照 $rk[1],rk[2],...,rk[n]$ 的顺序计算 $height$ ，就能以 $O(n)$ 的时间复杂度解决。

for(int i=1,j=0;i<=n;i++){
    if(rk[i]==1)continue; //height[1]=0
    if(j)j--;
	//height[rk[i]]>=height[rk[i-1]]-1
    while(s[i+j]==s[sa[rk[i]-1]+j])j++;
	//s[sa[rk[i]]+j]==s[sa[rk[i]-1]+j]
    h[rk[i]]=j;
}

引理二

\[lcp(sa[i],sa[j])=\min_{i+1\le k\le j}height[k] \]

或者换一种形式表达：

\[lcp(suf(i),suf(j))=\min_{rk[i]+1\le k\le rk[j]}height[k] \]

证明见此处。

有了引理二，我们就能把求任意两后缀的最长公共前缀问题转化为 RMQ 问题解决。

后缀数组的应用一

本部分主要是解决单串的问题。

两子串最长公共前缀

见上文引理二。

比较两子串大小关系

比较 $A=s[a,b],B=s[c,d]$ 的大小关系。

若 $lcp(a,c)>\min(|A|,|B|)$ ，则 $A<B \Longleftrightarrow |A|<|B|$ 。

否则，$A<B \Longleftrightarrow rk[a]<rk[c]$ 。

不同子串的数目

考虑子串就是后缀的前缀，若我们按照后缀排序的顺序，从 $sa[i-1]$ 到 $sa[i]$ 时，重复的前缀数量就是 $lcp(sa[i],sa[i-1])$ ，也就是 $height[i]$ 。这个结论比较显然就不证明了。容斥一下，答案即为 $\frac{n(n+1)}{2}-\sum_{i=2}^n height[i]$ 。

Luogu P2178 不同子串个数

SUBST1 - New Distinct Substrings

DISUBSTR - Distinct Substrings

对循环字符串的排序

[JSOI2007] 字符加密

这里的循环字符串指的是："abcd" -> "bcda" -> "cdab" -> "dabc"。

问题即为：给定一个长度为 $n$ 的初始字符串，对它的 $n$ 个循环字符串（包括它本身）排序。

求解是平凡的，只需要把原串复制一份接到原串后面做一遍后缀排序即可。注意最后判定的时候，起点要在原串中。

在线查询子串

见此处。

从字符串首尾取字符最小化字典序

[USACO07DEC] Best Cow Line G

省流：给你一个字符串，每次从首或尾取一个字符组成字符串，问所有能够组成的字符串中字典序最小的一个。

容易想到把原串翻转，接到原串后面，在二者中间加一个不在字符集中的字符，比如说 # 。后缀排序后，就可以快速在线地算出正串与反串的最长公共前缀了。

考虑两个指针 $p,q$，分别代表正向和反向取到哪了。终止条件即为 $p>q$ 。对于 $p,q$，若 $s[p]\ne s[q]$，显然取更小的那一个。否则，设 $len=lcp(suf(p),suf(q))$，取 $s[p+len],s[q+len]$ 中更小的那一个。

不可重叠最长重复子串

[USACO5.1]乐曲主题Musical Themes

二分长度 $k$ ，把 $h$ 数组划分成若干 $height[i]\ge k$ 的段。（如果有小于的就不考虑，直接扔掉）。二分时的判定：对于每段取位置（即 $sa[i]$ 的值）的 $\max$ 和 $\min$，如果 $\max -\min\ge k$，则说明存在长度为 $k$ 的不重叠的重复字串。时间复杂度 $O(n\log n)$。

另解：枚举每个 $i$ ，考虑判定 $height[i]$ 为子串长度时有没有解，通过单调栈预处理出左边和右边第一个小于 $height[i]$ 的位置。判定不重叠的方法可能会略微复杂。时间复杂度 $O(n\log n)$。代码见此处。

可重叠的 $k$ 次出现子串最大长度

[USACO06DEC] Milk Patterns G

直接看题，显然题目中的条件可以转化为有至少 $k$ 个后缀以这个子串作为公共前缀。那显然按照后缀排序后，就是连续的 $k$ 个后缀。相当于一个长度为 $k$ 的滑动窗口，然后求所有时刻中窗口的最小值的最大值。单调队列求解即可。

另解：先二分答案，然后将后缀分成若干组。判断有没有一个组的后缀个数不小于 $k$。如果有，那么存在 $k$ 个相同的子串满足条件，否则不存在。这个做法的时间复杂度为 $O(n\log n)$。

最长回文子串

更多细节参见集训队论文，不过感觉没啥用。如果不是忘记 Manacher 和 PAM 怎么写了，谁会用 SA 求最长回文字串呢？

最小循环节

更多细节参见集训队论文，不过感觉没啥用。谁会忘记 KMP 呢？

连续的若干个相同子串

连续若干个相同字串指的是一类问题。这类问题有一种 trick 解决，接下来以三道题为例。

[NOI2016] 优秀的拆分

分析问题，我们只需要求出每个位置作为形如 $AA$ 的字串的开头/结尾的方案数 $F_i,G_i$，最终答案即为 $\sum_{i=1}^{n-1} F_i \ G_{i+1}$。

直接求 $F_i,G_i$ 是困难的，这里介绍一种 trick：先枚举 $A$ 的长度 $len$ ，然后在把所有是 $len$ 的倍数的点记为关键点，显然一个 $AA$ 状的字串必定刚好覆盖两个关键点。

枚举相邻关键点，考虑覆盖这两个关键点的所有 $AA$ 串，并对 $F,G$ 贡献。

记 $i$ 为关键点，$j=i+len$。考虑求出 $suf(i),suf(j)$ 的 $lcp$ 和 $pre(i-1),pre(j-1)$ 的 $lcs$。

如下图，若 $lcp+lcs<len$，则无贡献。想一想，为什么？

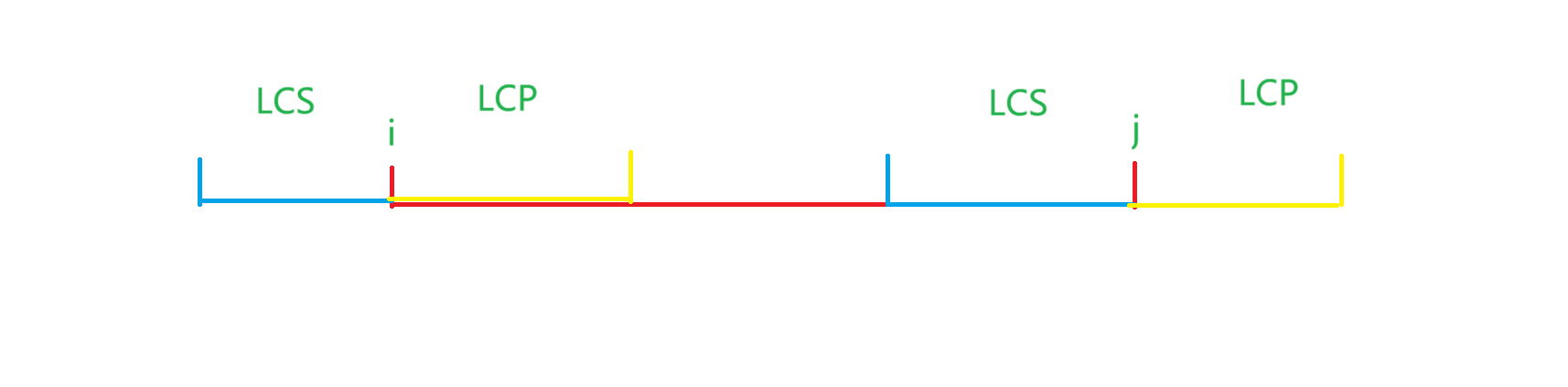
如下图，若 $lcp+lcs\ge len$，对 $F$ 的贡献即为紫色部分，对 $G$ 的贡献即为橙色部分，因为是区间加 $1$ ，差分统计即可。

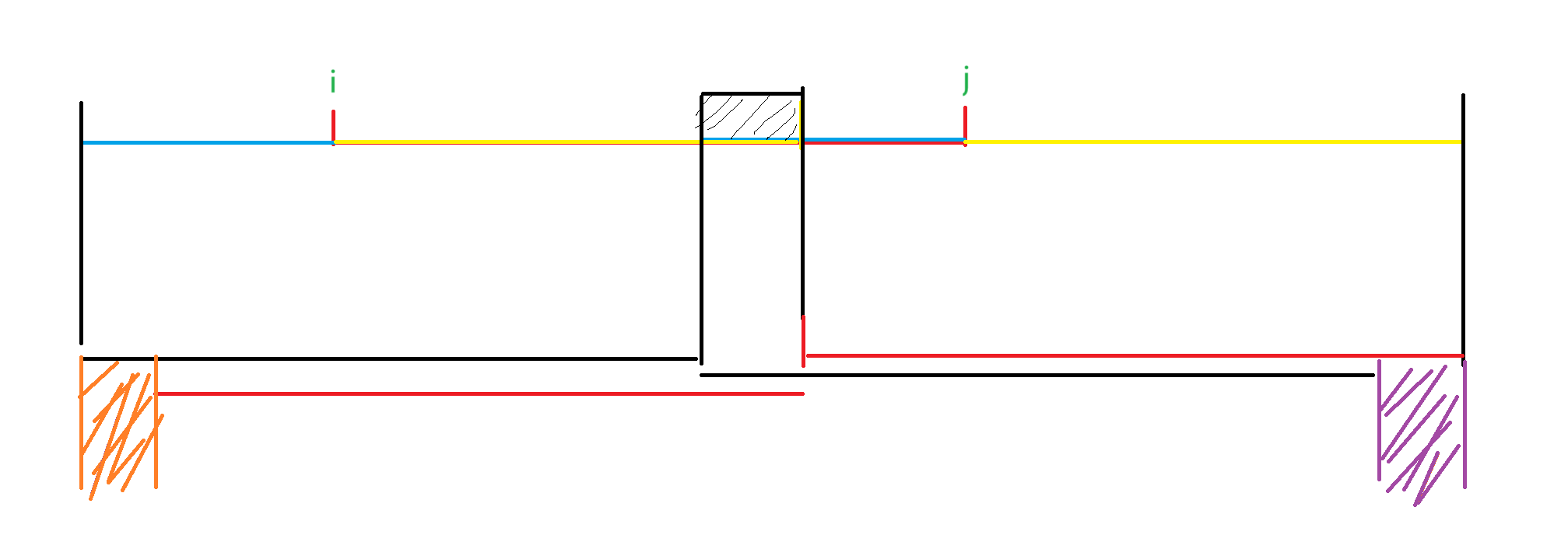
记得注意边界问题。请读者仔细体会这种 trick 的妙处，虽然笔者尚未完全体会到。

CF319D

容易发现，删除的过程是分阶段的。具体来说，可以一次性把相同长度的 $AA$ 串处理掉。

于是考虑枚举长度 $len$，因为每次处理都会使得总长减少 $len$，容易发现实际上需要处理的 $len$ 的数量是 $O(\sqrt n)$ 级别的。

接下来就直接把 trick 套上去即可，具体见此处。

SP687 REPEATS - Repeats

感觉很厉害！我不会！这里参考了 Alex_Wei 老师的题解。魏老师写得太好了，我就不写了！

写一下 Sol 3 这么做为什么是对的。

我们意识到，关键点怎么选都一样，重点在于让重复 $k$ 次的串覆盖 $k$ 次。比如说关键点集体移动了一定距离，但是 $tor,tol$ 是一起变的，换句话说，$tor+tol$ 的值不变。

我们发现，相邻点这样做（求出 $tor,tol$），求出的 $border$ 长度已经是极限了，所以是对的。

结合单调栈

[AHOI2013] 差异

一句话题意：求 $\sum_{1\le i,j\le n}lcp(suf(i),suf(j))$ 。

考虑在后缀意义下的 $lcp$ 为 $height$ 上连续一段的最小值。直接枚举 $i,j$ 做是困难的。我们反着考虑：当 $height[i]$ 作为最小值时的贡献。

容易想到使用单调栈维护 $i$ 左边/右边第一个小于等于 $height[i]$ 的位置。在这两个位置中的连续段被 $i$ 分成两段，其中 $height[i]$ 是这段中的最小值，左边长度 $\times$ 右边长度 $\times \ height[i]$ 即为 $height$ 上 $i$ 位置的贡献。

[HAOI2016] 找相同字符

一句话题意：给两个字符串 $s_1,s_2$，求 $\sum_{1\le i\le n_1}\sum_{1\le j \le n_2}lcp(suf_1(i),suf_2(j))$ 。

提供一个大常数做法：按套路把两串拼在一起。上式等价为：大串 $lcp$ 和 $-$ 两小串各自的 $lcp$ 和。分别把这三个东西求出来即可。$lcp$ 和的求法与上一题一样。

练习：

[NOI2015] 品酒大会：单调栈结合 ST 表，简单的 RMQ 问题。

结合并查集

[NOI2015] 品酒大会

还是这道题，一直不清楚并查集是怎么做的，今天来补一下。懒得自己写了，直接摘 OI Wiki 中的内容，反正讲得比我清晰：

某些题目求解时要求你将后缀数组划分成若干个连续 $lcp$ 长度大于等于某一值的段，亦即将 $height$ 数组划分成若干个连续最小值大于等于某一值的段并统计每一段的答案。如果有多次询问，我们可以将询问离线。观察到当给定值单调递减的时候，满足条件的区间个数总是越来越少，而新区间都是两个或多个原区间相连所得，且新区间中不包含在原区间内的部分的 $height$ 值都为减少到的这个值。我们只需要维护一个并查集，每次合并相邻的两个区间，并维护统计信息即可。

后缀数组的应用二

本部分主要涉及解决有关多串的问题。大部分内容来源于 2009 年的集训队论文。

最长公共子串

给定两个字符串，求它们的最长公共子串。

很容易想到把两个字符串拼在一起。然后 SA 做一下。枚举 $height$，取最大值。因为要求两个串的公共子串，所以如果 $sa[i]$ 和 $sa[i-1]$ 在不同的串内，则更新答案。

长度不小于 $k$ 的公共子串的个数

详见集训队论文。和品酒大会的第一问本质相同，这里就不赘述了。

不小于 $k$ 个字符串中的最长子串

给定 $n$ 个字符串，求出现在不小于 $k$ 个字符串中的最长子串

二分答案，然后将 $height$ 分组，判定每组后缀中是否有至少 $k$ 个来自互不相同的字符串中。

每个字符串至少出现两次且不重叠的最长子串

给定 $n$ 个字符串，求在每个字符串中至少出现两次且不重叠的最长子串。

在上文有提到求单串中的最长不重叠字串的做法：先二分答案 $k$，分组后判定是否不重叠，即位置的 $\max-\min$ 是否大于等于 $k$ 。

那么在多串中，我们先把所有串拼起来再二分答案，需要额外判定的是，是否每个字符串中都有至少两个后缀在这组里。

出现或反转后出现在每个字符串中的最长子串

与上例本质相同，我觉得论文加上这个完全是为了增加篇幅。

习题

[HEOI2016/TJOI2016] 字符串

本题主要考察可持久化线段树上二分。

容易发现，$s[a,b]$ 的任意子串与 $s[c,d]$ 的最长公共前缀等价于：$s[a,b]$ 的任意后缀与 $s[c,d]$ 的最长公共前缀。

暂时没啥思路，但很明显题中所求的是满足可二分性的，二分答案！

显然，二分答案的区间为 $[0,\min(b-a,d-c)+1]$ 。假设当前二分值为 $mid$，判定即为，是否存在一段开头在 $[a,b-mid+1]$ 的后缀，与 $suf(c)$ 的 $lcp$ 大于等于 $mid$ 。

直接做是困难的。考虑经典结论：$lcp(suf(i),suf(j))=\min_{rk_i+1\le k \le rk_j}height[k]$ 。这个结论有什么用呢？比如说我们现在有后缀 $suf(c)$，若某一后缀 $suf(i)$ 的名次 $rk_i$ 与 $rk_c$ 越接近，则 $lcp(suf(i),suf(c))$ 越大（单调不降）。

所以，我们要寻找 $rk[a,b-mid+1]$ 中，最接近 $rk_c$ 的值。因为有从左接近和从右接近两种情况，所以需要分类讨论一下。至于怎么求这个，熟练掌握主席树与线段树上二分的朋友们都会，但我全忘光了 /qd，求助 wf715 后才想起来。

LG P5353 树上后缀排序

本题主要考察基于倍增的后缀排序的本质。

好题。后缀平衡树板子，但用后缀排序解决的难度很高。写完后对后缀排序有了更深的理解。

首先要明白一点，后缀排序绝非局限于一个字符串：它可以在 $O(n\log n) $ 的时间复杂度下对 $n$ 个后缀进行排序，这些后缀不一定是要在一个字符串里的。

回到这题上，若不考虑字符串相等的情况，直接排序是平凡的：仿照一般的后缀排序，倍增求出每个节点的 $2^k$ 级祖先，因为后缀排序是基于倍增的，所以对 equal 函数进行修改即可。参考代码如下：

bool equal(int i,int j,int t){
	if(tp[i]==tp[j]&&tp[f[t][i]]==tp[f[t][j]])return 1;
	return 0;
}

其中函数 equal(i,j,t) 判断的是第 $i$ 个后缀与第 $j$ 个后缀在倍增到 $t$ 时是否相等。f[t][i] 表示 $i$ 的 $2^t$ 级祖先。

接下来考虑存在字符串相等的情况。题中给出：若存在相等的后缀，则先比较它们对应节点的父节点的排名，若仍然相等，则比较它们自身的编号。

突然发现自己不太会讲，下面给出代码：

void Rsort(int *sa,int *rk,int *tp,int m){
	for(int i=0;i<=m;i++)buc[i]=0;
	for(int i=1;i<=n;i++)buc[rk[i]]++;
	for(int i=1;i<=m;i++)buc[i]+=buc[i-1];
	for(int i=n;i>=1;i--)sa[buc[rk[tp[i]]]--]=tp[i];
}
bool equal(int i,int j,int t){
	if(tp[i]==tp[j]&&tp[f[t][i]]==tp[f[t][j]])return 1;
	return 0;
}
void get_SA(){
	int p;
	for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
	Rsort(sa,rk,tp,127);
	rk[sa[1]]=rk1[sa[1]]=p=1;
	for(int i=2;i<=n;i++){
		rk[sa[i]]=s[sa[i]]==s[sa[i-1]]?p:++p;
		rk1[sa[i]]=i;
	}
	for(int w=1,t=0;w<n;w<<=1,t++){
		for(int i=1;i<=n;i++)rk2[i]=rk1[f[t][i]];
		Rsort(tp,rk2,sa,n);
		Rsort(sa,rk,tp,p);
		for(int i=1;i<=n;i++)tp[i]=rk[i];
		rk[sa[1]]=rk1[sa[1]]=p=1;
		for(int i=2;i<=n;i++){
			rk[sa[i]]=equal(sa[i-1],sa[i],t)?p:++p;
			rk1[sa[i]]=i;
		}
	}
}

为什么要这样对 $tp$ 进行排序？为什么这样排就能符合题目要求？相信在看完代码后，你一定要这样的疑问。我们不妨来倒着想。

首先考虑在求 $sa$ 的过程中，有两个相等的后缀 $s_1,s_2$。因为它们相等，所以此时的 $rk$ 也相等，那么决定它们的次序的就是第二关键字 $tp$ 了，我们来进一步考虑 $tp$。

代码中对 $tp$ 的排序方式是：以上一轮的 $sa$ 作为第二关键字，以上一轮排序结果的后半段作为第一关键字，进行排序。其中依照 rk2 进行排序，满足了第一关键字字符串和第二关键字父亲编号，而 $sa$ 则满足了第三关键字自己编号。

所以对于 $sa$ 排序时，第二关键字 $tp$ 已经考虑了三个关键字了，因此是对的。

这里应该有一个归纳的思想：一开始对单个字符排序时，是符合题意的，接着对 $tp$，$sa$ 排序时，也是符合题意的，所以最终是符合题意的。

作为读者，自然想看想看顺畅的思路过程，但很可惜的是笔者并没有独立做出这道题。至于对于本题为什么要这么做，笔者尚无什么能成文的头绪，望读者不吝赐教。

LG P5346 【XR-1】柯南家族

还是树上后缀排序，xht 你坏事做尽！

树上后缀排序完后，求出 dfs 序后，这题就变成了静态区间第 $k$ 小问题，用主席树求解是平凡的。时间和空间复杂度均为 $O(n\log n)$ 。

[SCOI2012] 喵星球上的点名

本题主要考察如何数颜色。

考虑把名字串和询问串都拼起来，对每个询问串，在 $height$ 上二分出一个区间 $[l_i,r_i]$ 。

对于第一问，就是数 $[l_i,r_i]$ 中的颜色种数，建议参考 [SDOI2009] HH的项链。

对于第二问，我们可以先建立若干个区间，形如 $[i,nex_i-1]$，其中 $nex_i$ 表示 $i$ 右边最近的颜色为 $col_i$ 的位置。

那么对于一个颜色，它可以分为若干个连续且不相交的区间。区间 $[l,r]$ 的贡献即为 $\sum_{i}[l_i\le l\le r_i \le r]$ 。这样计算对于同种颜色是不重不漏的，画个图，想一想，为什么！

所以我们把这些区间同询问区间放在一起，按左端点 $l$ 从小到大排序，然后统计答案即可。特别注意：排序时，若 $l$ 相同，则询问区间应该在前面。这是很自然的，但容易忽略。

[NOI2023] 字符串

本题主要考察对条件的放缩和小学生都会的容斥。

很容易想到，如果题目要求的是小于等于的话，是很平凡的：先后缀排序，再二维数点即可。

但是会有相等的情况，所以我们考虑容斥，把相等的部分减掉！正串反串相等即是回文串，因此我们可以先对每个点为中心求出极长回文子串。接着画个图分析一下：

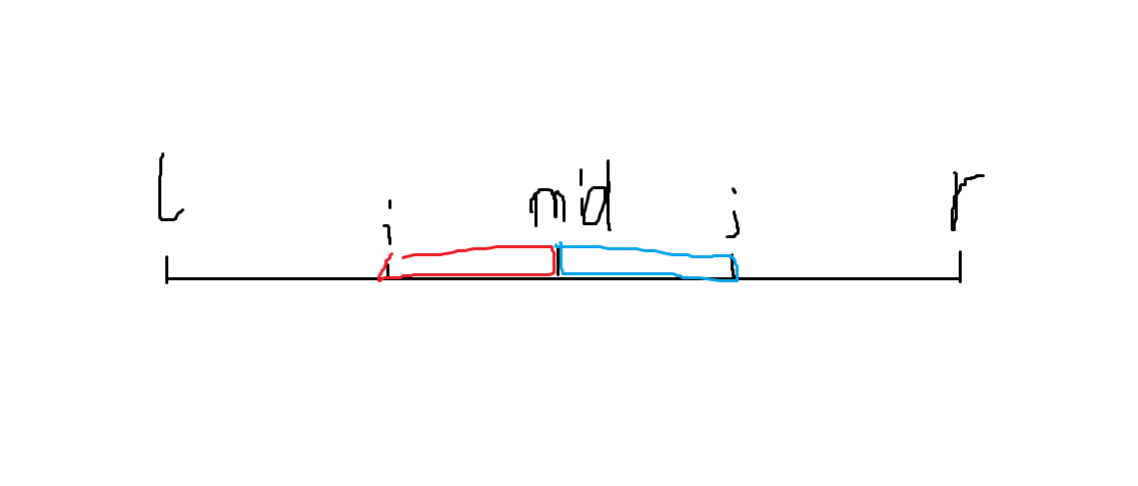
如上图容易发现，在回文串中，恒有 $rk_{i}<rk_{resever(j)}\Longleftrightarrow rk_l<rk_{reserve(r)}$，因此我们只需要统计 $rk_{l}<rk_{reserve(r)}$ 的回文中心即可。不过还要满足 $l\le i$，二维数点即可。

如此代码能力，无颜学 OI！

更新日志

2024.2.12 基本写完了。

2024.2.13 13:40 更新了一道习题。

2024.2.20 17:28 更新了一道习题。

2024.2.21 17:50 更新了一道习题。

2024.2.22 12:58 更新了一道习题。

2024.2.23 21:47 更新了一道习题。

后记

其实一年前就写了一点，后面脱离训练了很久，总体上快有一年了。今年春节后才开始继续认真训练。只剩一年多一点了，希望大家都能有一个好的结局。

posted @ 2024-02-12 22:38 Luminescence_2024 阅读(111) 评论(1) 收藏举报

刷新页面返回顶部