网络流学习笔记
零、基本概念
直接走 OIwiki 或者看蓝书吧。
一、最大流
1. Ford-Fulkerson 增广
“该方法运用贪心的思想,通过寻找增广路来更新并求解最大流。”
主要流程就是每次选一些增广路,以来更新最大流。但这个贪心思路不一定能保证正确性。Ford-Fulkerson 增广的核心技术是通过设置 反向边 来实现 反悔贪心。
反向边的特性:流量与正向边互为相反数,且始终不大于零。
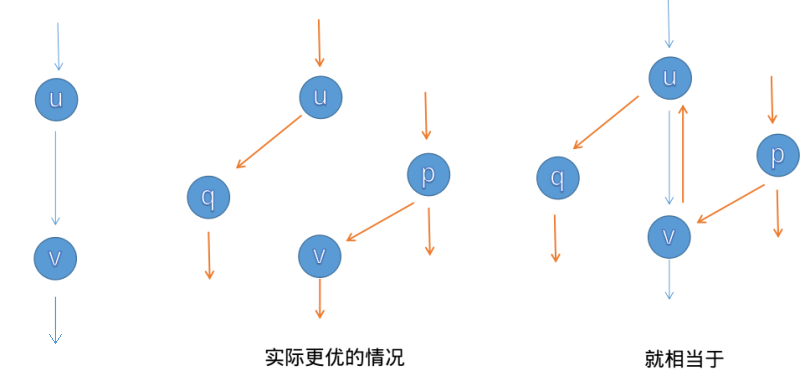
以下的 Edmonds-Karp、Dinic 和 ISAP 都是基于 Ford-Fulkerson 增广的算法。
2. Edmonds-Karp
基本流程:每次用 Bfs 选择边数最少的一条增广路,如此反复,直到没有增广路。
时间复杂度:可以证明,增广总轮数的上界为 \(O(nm)\),单次 Bfs 的时间复杂度为 \(O(m)\),因此总复杂度为 \(O(nm^2)\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 205, MAXM = 5005;
int n, m, s, t, head[MAXN], pre[MAXN];
ll f[MAXN], maxflow;
bool vst[MAXN];
struct node{
int to, nxt;
ll wi;
} edge[MAXM*2];
inline void Add_edge(int i, int from, int to, int wi){
edge[i].to = to;
edge[i].wi = wi;
edge[i].nxt = head[from];
head[from] = i;
return;
}
inline bool Bfs(){
memset(vst, false, sizeof(vst));
memset(f, 0x3f3f, sizeof(f));//f:到当前节点为止,增广路上的最小边
queue<int> que; que.push(s); vst[s] = true;
while(!que.empty()){
int cur = que.front(); que.pop();
for(int i = head[cur]; i; i = edge[i].nxt){
if(!edge[i].wi) continue;
int to = edge[i].to;
if(vst[to]) continue;
f[to] = min(f[cur], edge[i].wi);
pre[to] = i;
vst[to] = true;
que.push(to);
if(to == t) return true;
}
}
return false;
}
inline void Update(){
for(int x = pre[t]; x; x = pre[edge[x^1].to])
edge[x].wi -= f[t], edge[x^1].wi += f[t];
maxflow += f[t];
return;
}
int main(){
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int ui, vi, wi; scanf("%d%d%d", &ui, &vi, &wi);
Add_edge(i*2, ui, vi, wi); Add_edge(i*2+1, vi, ui, 0);
}
while(Bfs()) Update();
cout<<maxflow;
return 0;
}
3. Dinic 算法
基本思想:注意到每次 EK 算法都在试着找一条边数最少的增广路。那么假如说现在有一个图,它到 \(t\) 的每一条路径的边数都是最少,可以证明这时 EK 的复杂度仅有 \(O(nm)\)。
基本流程:增广直到不存在增广路。每次增广时,先使用 Bfs 在残量网络上求出一个“分层图”(就是一个 DAG,满足每条边仅指向 Bfs 的下一层,满足上面所说的每条路径等长最小),然后用 EK 求分层图最大流,顺便就可以更新剩余容量。
优化:
-
后继完全增广完毕的点不访问。【常数优化】
-
当前弧优化:去掉已经增广过了的出边(代码中的 now 数组)。【复杂度优化】
-
Dfs 代替 EK 找分层图最大流:由于分层图的特殊性,这里使用 Dfs 可以得到一个常数更小、复杂度也一样的算法。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 205, MAXM = 5005;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int n, m, s, t, head[MAXN], now[MAXN], d[MAXN];
//d:用于记录 bfs 层数,以建立分层图
struct node{
int to, nxt;
ll wi;
} edge[MAXM<<1];
inline void Add_edge(int i, int from, int to, int wi){
edge[i].to = to;
edge[i].wi = wi;
edge[i].nxt = head[from];
head[from] = i;
return;
}
inline bool Bfs(){
memset(d, 0, sizeof(d));
for(int i = 1; i <= n; i++) now[i] = head[i];
queue<int> que; que.push(s); d[s] = 1;//注意给 d[s] 赋初值,以免下方 BFS 卡死
while(!que.empty()){
int cur = que.front(); que.pop();
for(int i = head[cur]; i; i = edge[i].nxt){
if(!edge[i].wi) continue;
int to = edge[i].to;
if(d[to]) continue;
d[to] = d[cur]+1;
que.push(to);
if(to == t) return true;
}
}
return false;
}
inline ll Dinic(int x, ll flow){
if(x == t) return flow;
ll rest = flow;
for(int i = now[x]; i and rest; i = edge[i].nxt){//注意要保持 rest > 0
now[x] = i;//当前弧优化(请格外注意这里,老版蓝书上的写法有误!)
int to = edge[i].to;
if(!edge[i].wi) continue;
if(d[to] != d[x]+1) continue;
ll tmp = Dinic(to, min(rest, edge[i].wi));
if(!tmp) d[to] = 0;//去掉接下来没有可增广的点
rest -= tmp;
edge[i].wi -= tmp;
edge[i^1].wi += tmp;
}
return flow-rest;
}
int main(){
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int ui, vi, wi; scanf("%d%d%d", &ui, &vi, &wi);
Add_edge(i*2, ui, vi, wi); Add_edge(i*2+1, vi, ui, 0);
}
ll maxflow = 0;
while(Bfs()) maxflow += Dinic(s, INF);
cout<<maxflow;
return 0;
}
时间复杂度:
-
一般情况:可证明单轮增广复杂度为 \(O(nm)\),一次 Bfs 复杂度为 \(O(m)\),增广总轮数不超过 \(O(n)\),总复杂度为 \(O(n(nm+m))\),在稠密图中表现优异。
-
单位容量网络(边权都为 0/1):\(O(m \min (m^{\frac{1}{2}}, n^{\frac{2}{3}}))\)。
-
单位容量网络 + 除了源、汇点外,出或者入度为 1(即求 二分图最大匹配 时的网络):\(O(m\sqrt{n})\)。
4. ISAP 算法
基本思想:ISAP 可看作对 Dinic 的常数优化。在 Dinic 中,每次求完分层图的最大流时,都需要 Bfs 一次。而 ISAP 的思想就是:每次增广时实时更新分层图,就只需要在开头进行一次 Bfs 即可。
基本流程:
-
进行第一次 Bfs,在反向图上,处理一个以 t 为起点的 d 数组。(因为)
-
执行 Dfs,直到 d[s] > n:
-
前面与 Dinic 一模一样。
-
如果当前节点 x 被完全增广了(即流入量还有剩余),那么尝试更新 d[x]:
访问 x 的每一条出边,求它后继的 d 数组最小值,并将 d[x] 设置为最小值加一。
-
如果找不到任何一个后继,将 d[x] 设置为 n+1。
-
否则更新 d[x],重置当前弧优化数组 now[x]。
-
-
点击查看代码
inline void Bfs(){
queue<int> que; que.push(t); d[t] = 1;
for(int i = 1; i <= n; i++) now[i] = head[i];
while(!que.empty()){
int cur = que.front(); que.pop();
for(int i = head[cur]; i; i = edge[i].nxt){
int to = edge[i].to;
if(d[to]) continue;
d[to] = d[cur]+1;
que.push(to);
}
}
return;
}
inline void Update(int x){
int nd = n+1;
for(int i = head[x]; i; i = edge[i].nxt)
if(edge[i].ci) nd = min(nd, d[edge[i].to]+1);
d[x] = nd;
now[x] = head[x];
return;
}
inline ll ISAP(int x, ll flow){
if(x == t) return flow;
ll rest = flow;
bool flag = false;
for(int i = now[x]; i and rest; i = edge[i].nxt){
if(!edge[i].ci) continue;
int to = edge[i].to;
if(d[to]+1 != d[x]) continue;
now[x] = i;
ll k = ISAP(to, min(rest, edge[i].ci));
edge[i].ci -= k;
edge[i^1].ci += k;
rest -= k;
}
if(rest) Update(x);
return flow-rest;
}
还有另一种写法,可以减少码量:在 update 函数中,只需要将 d[x]++ 即可。
这个时候就有人(比如我)要问了:为什么可以这样?按照原本来说,d[x] 不一定只增加 1 啊?
但若 d[x] 在此处的增加不合法的话,下一次迭代到 x,它会再次 +1,一直迭代直到合法为止。
这个时候又有人要问了:那这样常数好大啊!
但原本 update 函数的常数就很大啊:要访问 x 的每一条出边。因此不分伯仲罢了。
除了当前弧优化外,ISAP 还有一种优化:GAP 优化。记录每一种 d 数组的每一个值的数量 gap[d[x]]。当更新 d 时出现一个 gap[d[x]] 变成 0,那么说明出现了 “断层”,可以推断出增广已经结束。
inline void Update(int x){
if(--gap[d[x]] == 0) {END = true; return;}
++gap[++d[x]];
now[x] = head[x];
return;
}
5. 例题
- P2766 最长不下降子序列问题:点化边的技巧:拆为入点 & 出点,在二者之间的边权代表取次数的限制。
二、最小割
1. 定义 & 定理
一种点的划分方式(或者说边集):将所有的点划分为 \(S, T\) 两部分,其中源点 \(s \in S, t \in T\)。
割的容量:所有从 \(S\) 连接到 \(T\) 的边的容量之和。
最小割:求得一个割使得该割容量最小。或者说,在一个网络中删去一些边使得该图 \(s, t\) 不连通,并使这些边的容量之和最小。
最大流最小割定理:最大流 = 最小割。感性地反证一下,最小割如果小于最大流,则删去最小割后仍存在增广路,那么最小割并没使图不连通,所以最小割大于等于最大流,相等时最大流取最大、最小割取最小。【详细证明:here,我会回来看的。】
构造最小割:在求完最大流之后,在剩下的残量网络中,源点能到达的点 与 不能到达的点 之间的所有边。(明显,这些边的和即为最大流。)
2. 例题
- 有线电视网:网络流建模的 边点互换 和 INF 防割断 技巧。点转边:拆为入点 + 出点,边转点:加一个点即可。还有求多源点多汇点最小割技巧:枚举源点汇点即可。
三、费用流
1. 概念
网络上每条边不但有容量限制 \(c\),还有一个单位流量的费用 \(w\)。当该边的流量为 \(f\) 时,该边的费用就为 \(f \times w\)。
该网络中总费用最小的最大流称为 最小费用最大流,同理还有最大费用最大流,合称费用流。
注意,费用流一定是建立在最大流的基础上的。
2. 算法
费用流的主流算法为 SSP 算法,一般来说就已经够用了。【详见:关于网络流费用流算法复杂度】
SSP 仍旧是基于 Ford-Fulkerson 增广求最大流的,反边容量设置为 0、费用设置为相反数。只不过在寻找增广路时,它并不是像 EK、Dinic 那样选择边数最少的那一条,而是选择费用最少的一条。正确性是显然的。
所以,实现时只要把 EK 或 Dinic 的 Bfs 部分换成 SPFA 就可以了。(因为有反向边有负边权,就不能用 dijkstra。(有结论:如果一开始的图上不存在负环,以后任意时刻图都不会存在负环。如果存在负环,我们也有办法解决,具体见后文上下界网络流处。))
由于失去了 Bfs 的复杂度保证,这里的复杂度只能做到 FF 增广任选路径时的复杂度:设最终求出最大流的值为 \(f\),那么增广轮数最差为 \(O(f)\),单次增广最差为 \(O(mn)\),总复杂度为 \(O(nmf)\)。(这种关于值域的多项式复杂度被称为 伪多项式复杂度。)
具体实现建议直接以原本 EK 为框架,不用写 Dinic 了。因为反正都失去了 Bfs 的复杂度保证,EK、Dinic 实现的 SSP 版本实际复杂度没有什么区别。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 5005, MAXM = 5e4+5;
int n, m, s, t, head[MAXN], pre[MAXN];
bool inq[MAXN];
ll w[MAXN], c[MAXN], maxflow, mincost;
struct node{
int to, nxt;
ll ci, wi;
} edge[MAXM<<1];
inline void Add_edge(int i, int from, int to, int ci, int wi){
edge[i] = (node){to, head[from], ci, wi}, head[from] = i;
return;
}
inline bool SPFA(){
memset(c, 0x3f3f, sizeof(c));
memset(w, 0x3f3f, sizeof(w));
queue<int> que; que.push(s);
w[s] = 0, pre[t] = 0;//inq[s] 可以不标,pre[t] 用于判断有无解
while(!que.empty()){
int cur = que.front(); que.pop();
inq[cur] = false;
for(int i = head[cur]; i; i = edge[i].nxt){
int to = edge[i].to;
//怎么求出一条路径的最小费用?怎么找到一条最小费用路?
//直接相加费用就可以了
//因为增长流量在路上每一处都是相等的,满足分配律
if(!edge[i].ci or w[to] <= w[cur]+edge[i].wi) continue;
w[to] = w[cur]+edge[i].wi;
c[to] = min(c[cur], edge[i].ci);
pre[to] = i;
// if(to == t) return true;不能这么写,因为 SPFA 不能直接确定最短
if(!inq[to]) que.push(to), inq[to] = true;
}
}
return pre[t];
}
inline void Update(){
for(int i = pre[t]; i; i = pre[edge[i^1].to]){
edge[i].ci -= c[t], edge[i^1].ci += c[t];
mincost += edge[i].wi*c[t];
}
maxflow += c[t];
return;
}
int main(){
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int ui, vi, ci, wi; scanf("%d%d%d%d", &ui, &vi, &ci, &wi);
Add_edge(i*2, ui, vi, ci, wi); Add_edge(i*2+1, vi, ui, 0, -wi);
}
while(SPFA()) Update();
cout<<maxflow<<" "<<mincost;
return 0;
}
四、上下界网络流
1. 概述
就是每条边的流量必须满足 \(b(u, v) \le f(u, v) \le c(u, v)\) 的限制。分为无源汇上下界可行流、有源汇上下界可行流、有源汇上下界最大流、有源汇上下界最小流。
2. 无源汇上下界可行流
可行流的题目一般要求我们判断是否有解,当然也可以套一个费用流,变成“有/无源汇上下界最小费用可行流”。
大体思路是先给每条边流入 \(b(u, v)\) 的流量,然后考虑怎么去调整使得流量可以满足流量守恒。
我们定义新变量 \(f'(u, v) = f(u, v) - b(u, v)\),\(c'(u, v) = c(u, v) - b(u, v)\)。
满足流量守恒,即对于每个位置 \(u\),我们需要有:
令 \(\Delta_u = \sum_{(v, u) \in E} b(v, u) - \sum_{(u, v) \in E} b(u, v)\)。
我们建立一个超级源点 \(s_0\) 和一个超级汇点 \(t_0\),二者用来控制流量平衡:
-
若 \(\Delta_u > 0\),则向 \(t_0\) 连一条容量为 \(\Delta_u\) 的边,表示该点须额外流出 \(\Delta_u\) 的流量;
-
若 \(\Delta_u < 0\),则从 \(s_0\) 连一条容量为 \(|\Delta_u|\) 的边,表示该点须额外流入 \(|\Delta_u|\) 的流量。
3. 有源汇上下界可行流
实际和无源汇的情况基本差不多。我们只需要在原源汇 \(t, s\) 之间添加一条边,满足 \(c(t, s) = +\inf, b(t, s) = 0\) 即可。
4. 有源汇上下界最大流
先跑一遍有源汇上下界可行流,然后去掉所有附加边(\(s_0, t_0\) 的边、\(t, s\) 之间的 \(+\inf\) 边)再跑一次 \(s \rightarrow t\) 的最大流。
5. 有源汇上下界最小流
有两种写法:
-
先跑一遍有源汇上下界可行流,然后去掉所有附加边再跑一次 \(t \rightarrow s\) 的最大流,用原先 \(\inf\) 边中的流量减去 \(t \rightarrow s\) 的最大流。
-
先不连接 \(t, s\) 之间的 \(+\inf\) 边跑一次有源汇上下界可行流,连上后再跑一次,取最终 \(\inf\) 边中的流量。
感性理解一下应该都不难。
6. 有负环的一般费用流
先将每条负权边满流,然后我们建立形如 \((v, u, c(u, v), -w(u, v))\) 的新边,表示退掉流量的贡献。接着用类似有源汇上下界最大流的方法连附加边以及跑两次费用流就可以了。
五、最小割树
reference: 《浅谈无向图最小割问题的一些算法及应用》(绍兴一中王文涛,2016 年国集论文)、@Eznibuil 的题解
感觉论文的一大问题是为了严谨性而忽略了简明性,故在此用尽量清晰的语言重新梳理一遍论文的思路。(写完以后发现怎么几乎和论文一样呢?。。。)
1. 描述
P4897 【模板】最小割树(Gomory-Hu Tree)
给定一个无向连通图,多次查询,询问不同源点汇点间的最小割。(既然能查询最小割,那肯定也可以查询最大流。)
2. Gusfield 算法(等价流树算法)
我知道上面的那道板子题叫作 Gomory-Hu Tree,但是题解区里面大部分用的其实都是 Gusfield 算法。Gusfield 算法较真正的 Gomory-Hu 算法更简明易懂,但 Gomory-Hu 算法较 Gusfield 算法多出了输出最小割方案的功能。
所以 Gusfield 算法是什么呢?它可以构建出来一棵 \(n\) 个点的树,即等价流树。其满足树上任意两点 \(s, t\) 之间的最小割都等于它们在树上的最小割(即树上 \(s, t\) 路径之间最小的边权)。显然,如果我们构建出来了这棵树,我们就可以在每次询问时用树上信息维护的技巧查询任意两点之间的最小割了。
所以这个算法具体是怎么进行的呢?很简单,使用分治法。一开始我们先随意选两个点 \(s, t\),求出二者之间的最小割,然后在等价流树上连接 \((s, t)\),边权为最小割。接着根据最小割将点集划分为分别与 \(s, t\) 连通的两部分,往下分治。当分治的点集只剩下一个点时,分治终止。
需要注意的是,等价流树并不满足将边 \(u, v\) 断开后,其分出的两个连通块即为最小割分出的两个连通块;这里求最小割的时候也只能在 原图 上跑,不能只在当前分治到的点集上跑。这些问题的原因在后面介绍 Gomory-Hu 算法时会解释。
接下来我们将着手证明该算法的正确性(可能看上去有点长,你可以只看看引理,跳过证明)。
在开始之前,我们先做一些符号约定:
令图 \(G = (V, E)\)。
定义 \(G\) 的一个割为点集 \(V\) 的一个划分 \((U, V-U)\)。
对于一个割,若 \(u \in U, v \in V-U\),则可以称 \(U\) 为 \(u\) 侧,\(V-U\) 为 \(v\) 侧。
定义这个割的边集为所有满足 \(u \in U, v \in V-U\) 的边 \((u, v)\) 的集合,记作 \(\delta(U)\)。
定义割的权值为其边集的权值和,记作 \(c(U)\)。
定义 \(\alpha(u, v)\) 表示 \(u, v\) 之间最小割的边集,\(\lambda(u, v)\) 表示 \(u, v\) 之间的最小割的权值。
引理 1:对于任意不同的三点 \(a, b, c\),有 \(\lambda(a, b) \ge \min(\lambda(a, c), \lambda(c, b))\)。
其实这个引理等价于 \(\lambda(a, b), \lambda(a, c), \lambda(c, b)\) 中两个较小者相等。
证明:很显然,不妨设 \(\lambda(a, b)\) 最小。如果 \(c\) 在 \(a\) 侧,则 \(\lambda(b, c) = \lambda(b, a)\);反之则 \(\lambda(a, c) = \lambda(a, b)\)。
然后这个引理可以推广:
对于任意不同的两点 \(u, v\),有 \(\lambda(u, v) \ge \min(\lambda(u, w_1), \lambda(w_1, w_2), \dots, \lambda(w_k, v))\)。
引理 2:割的权值函数 \(c(U)\) 为子模函数(submodular),即 \(c(A) + c(B) \ge c(A \cup B) + c(A \cap B)\)。
引理 3:割的权值函数 \(c(U)\) 为反模函数(posi-modular),即 \(c(A) + c(B) \ge c(A \setminus B) + c(A \setminus B)\)。
证明:

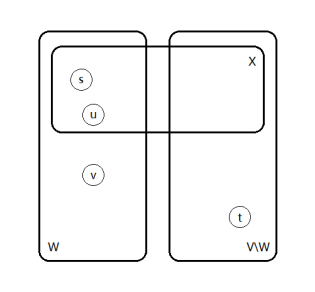
这是论文里面的图。对着这张图数一下边就容易证明了。
引理 4:设 \(W\) 为 \(\alpha(s, t)\) 的一侧,则对于任意不同的 \(u, v \in W\),存在一个 \(u, v\) 的最小割 \(\delta(X)\) 使得 \(X \subseteq W\)。
这个引理十分关键,因为它指出了最小割的不相交性。
证明:
(嘻嘻嘻又是论文里的图 orzorzorz)
不妨设 \(u \in X, s \in X\)。接着我们分 \(t\) 所在的位置进行讨论:
-
\(t \in X\):
据引理 2 易得:
\[\begin{aligned} & c(W) + c(X) \ge c(W \cup X) + c(W \cap X) \\ \Rightarrow & c(W \cap X) \le c(X) + c(W) - c(W \cup X) \le c(X) \end{aligned} \] -
\(t \not \in X\):
据引理 3 易得:
\[\begin{aligned} & c(W) + c(X) \ge c(W \setminus X) + c(X \setminus W) \\ \Rightarrow & c(W \setminus X) \le c(X) + c(W) - c(X \setminus W) \le c(X) \end{aligned} \]
引理 5:对于等价流树上的两点 \(u, v\),设其路径上的最小边为 \((x, y)\),则 \(\lambda(u, v) = \lambda(x, y)\)。
根据引理 1 的推广,显然有 \(\lambda(u, v) \ge \lambda(x, y)\)。于是我们只需要证明 \(\lambda(u, v) \le \lambda(x, y)\)。
发现如果我们考虑 \(u, v\) 与 \(\alpha(x, y)\) 的关系的话,实际不好讨论 \(u, v\) 在同一侧时的情况。根据分治构造法,容易发现 \(u, v\) 的树路径上一定存在某条边 \((s, t)\),满足 \(\alpha(s, t)\) 也为 \(u, v\) 的割。我们不妨设 \(u\) 在 \(s\) 侧、\(v\) 在 \(t\) 侧。
于是我们接下来需要证明 \(\lambda(u, v) \le \min(\text{u, s 树路径间最小边}, \lambda(s, t), \text{v, t 树路径间最小边})\)。使用数学归纳法,假设引理 5 对于 \(u, s\) 以及 \(v, t\) 都成立,即有 \(u, s\) 树路径间最小边 \(= \lambda(u, s)\),\(t, v\) 树路径间最小边 \(= \lambda(t, v)\)。
于是我们接下来需要证明 \(\lambda(u, v) \le \min(\lambda(u, s), \lambda(s, t), \lambda(t, v))\)。
由于 \(\alpha(s, t)\) 也为 \(u, v\) 的割,所以 \(\lambda(u, v) \le \lambda(s, t)\) 显然成立。
然后我们考虑 \(\lambda(u, s)\)(\(\lambda(v, t)\) 同理)。根据引理 4,\(\alpha(u, s)\) 的两侧中一定有一侧满足 \(\subseteq\) \(\alpha(s, t)\) 的 \(s\) 侧,故我们接下来分类讨论 \(u, s\) 哪一侧满足条件。
-
\(\alpha(u, s)\) 的 \(u\) 侧 \(\subseteq\) \(\alpha(s, t)\) 的 \(s\) 侧
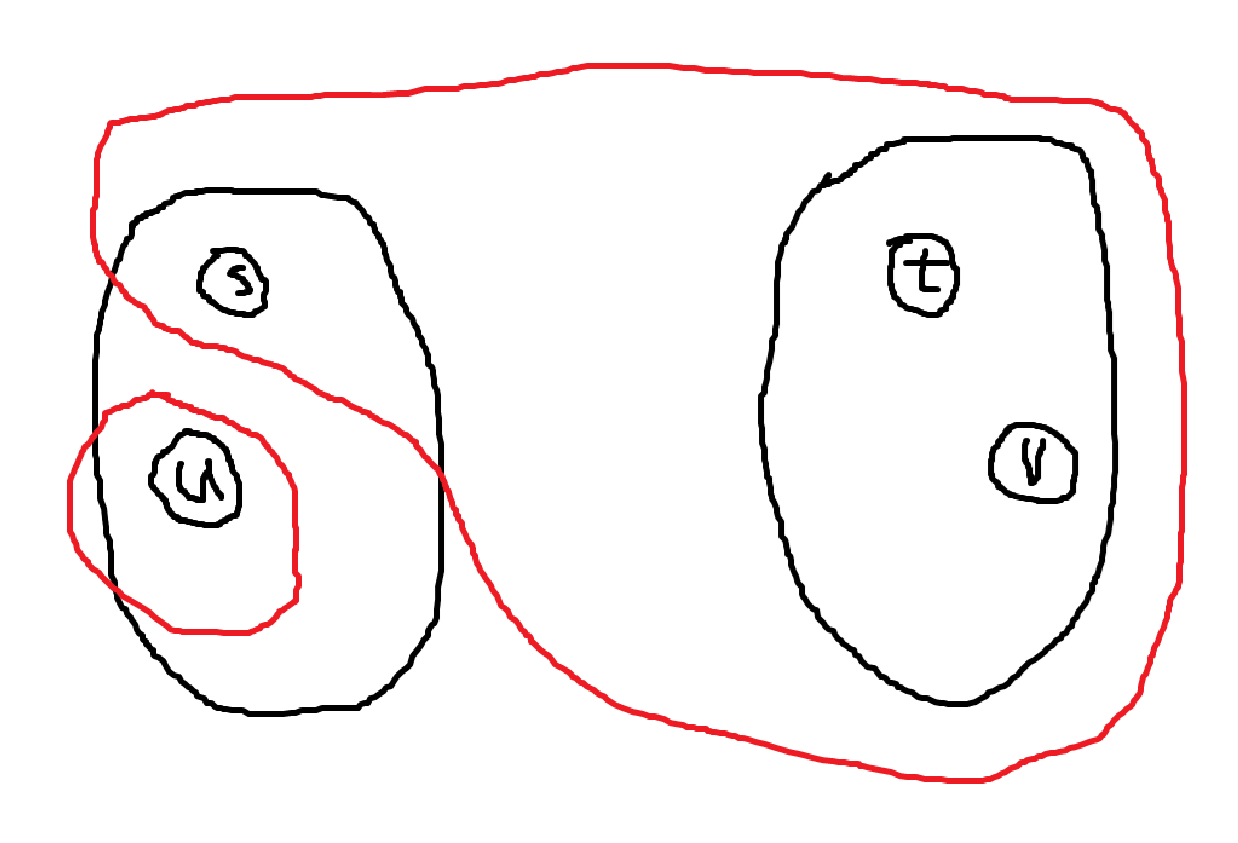
显然 \(\alpha(u, s)\) 也为 \(u, v\) 的割,故 \(\lambda(u, v) \le \lambda(u, s)\)。
-
\(\alpha(u, s)\) 的 \(s\) 侧 \(\subseteq\) \(\alpha(s, t)\) 的 \(s\) 侧
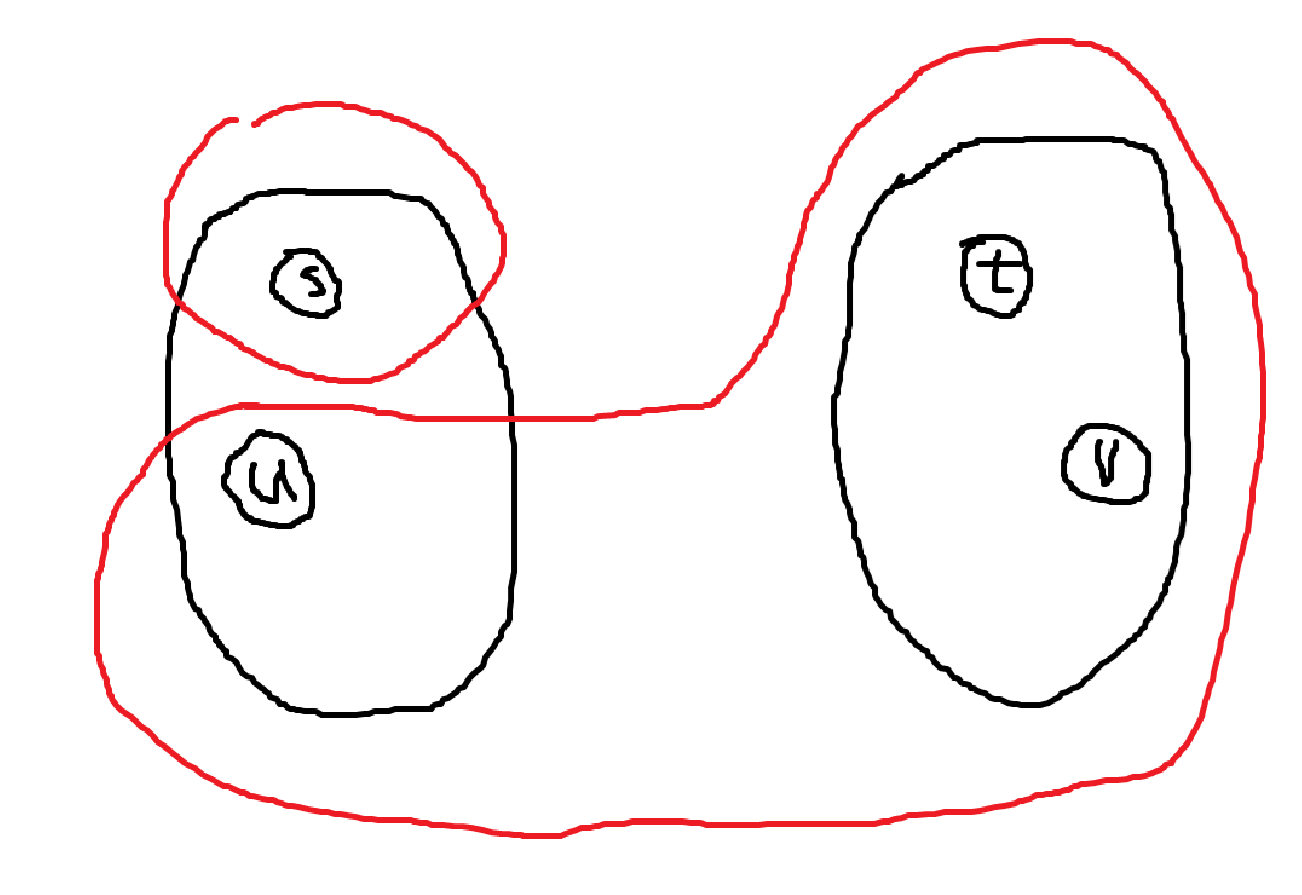
显然 \(\alpha(u, s)\) 也为 \(s, t\) 的割,故 \(\lambda(u, v) \le \lambda(s, t) \le \lambda(u, s)\)。
正确性已经有保证了!下面是代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 505, MAXM = 1505, INF = 0x3f3f3f3f;
int n, m, q, e = 1, s, t, head[MAXN], col[MAXN];
struct node{
int to, nxt, ci;
} edge1[MAXM<<2], edge2[MAXM<<2];
inline void Add_Edge(int u, int v, int c){
edge1[++e] = {v, head[u], c}, head[u] = e;
edge1[++e] = {u, head[v], 0}, head[v] = e;
return;
}
//-----
int d[MAXN], now[MAXN];
inline bool BFS(){
for(int i = 0; i <= n; i++) d[i] = 0, now[i] = head[i];
queue<int> que;
que.push(s); d[s] = 1;
while(!que.empty()){
int x = que.front(); que.pop();
for(int i = head[x]; i; i = edge2[i].nxt){
int to = edge2[i].to;
if(d[to] or !edge2[i].ci) continue;
d[to] = d[x]+1;
que.push(to);
if(to == t) return true;
}
}
return false;
}
inline int DFS(int x, int flow){
if(x == t) return flow;
int rest = flow;
for(int i = now[x]; i and rest; i = edge2[i].nxt){
int to = edge2[i].to;
now[x] = i;
if(!edge2[i].ci) continue;
if(d[to] != d[x]+1) continue;
int tmp = DFS(to, min(rest, edge2[i].ci));
if(!tmp) d[to] = 0;
rest -= tmp, edge2[i].ci -= tmp, edge2[i^1].ci += tmp;
}
return flow-rest;
}
inline int Dinic(){
for(int i = 1; i <= e; i++) edge2[i] = edge1[i];
int maxflow = 0;
while(BFS()) maxflow += DFS(s, INF);
return maxflow;
}
//-----
int fa[MAXN], w[MAXN];
inline int Query(int x, int y){
if(d[x] < d[y]) swap(x, y);
int ans = INF;
while(d[x] > d[y]) ans = min(ans, w[x]), x = fa[x];
while(x != y) ans = min(ans, min(w[x], w[y])), x = fa[x], y = fa[y];
return ans;
}
//-----
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
int u, v, w; scanf("%d%d%d", &u, &v, &w);
Add_Edge(u, v, w), Add_Edge(v, u, w);
}
for(int i = 0; i <= n; i++) col[i] = 1;//col[i] 表示 i 当前在哪个点所对应的连通块中。
for(int i = 1; i <= n; i++){//是的,其实我们可以不用真的用分治来实现。
s = i, t = col[i];
fa[s] = t, w[s] = Dinic();
for(int j = 0; j <= n; j++) if(d[j] and col[j] == t) col[j] = s;
}
for(int i = 1; i <= n; i++) d[i] = d[fa[i]]+1;
scanf("%d", &q);
while(q--){
int u, v; scanf("%d%d", &u, &v);
printf("%d\n", Query(u, v));
}
return 0;
}
时间复杂度:\(O(n^3m)\)。
3. Gomory-Hu(郭沫若 - 胡)算法
所以本质上是什么导致了 Gusfield 算法求出来的等价类树不能做到切开一条边就能得到对应的最小割呢?
其实就是上面我们在证明引理 5 的时候讨论的那两种情况。
如图所示:

第一次分治时,我们选择 \(\alpha(s, t_1)\)。第二次分治时,有可能出现新 \(s\) 侧与原本的 \(t_1\) 侧完全没有相连的情况。也就是说,这里我们建出的等价流树形如 \(t_2 - s - t_1\),但 Gomory-Hu 树本应形如 \(s - t_2 - t_1\)。
所以,我们不能每一次粗暴地将最小割的源汇点在树中连起来就可以了。我们需要在 \(s\) 侧与 \(t\) 侧中分别找一个合适的点代表这两个连通块,在树中连起来。
这两个点(设为 \(u, v\),\(x\) 在 \(u\) 侧,\(v\) 在 \(t\) 侧)需要满足如下的条件:
-
一直到分治终止时,都没有任何后续的最小割割开 \(u, t\)、\(s, v\)。
-
\(\lambda(u, v) = \lambda(s, t)\)。
引理 6:如果 \(u, v\) 满足条件 1,则一定满足条件 2。
证明:

(其实和上面 Gusfield 算法的正确性证明是差不多的,你看这图也一模一样)
由于 \(\alpha(s, t)\) 也为 \(u, v\) 的割,所以 \(\lambda(u, v) \le \lambda(s, t)\)。故我们只需要证明 \(\lambda(u, v) \ge \lambda(s, t)\)。
由于 \(\alpha(u, s)\) 也为 \(s, t\) 的割,所以 \(\lambda(s, t) \le \lambda(u, s)\)。同理,\(\lambda(s, t) \le \lambda(t, v)\)。
根据引理 1 的推广,\(\lambda(u, v) \ge \min(\lambda(u, s), \lambda(s, t), \lambda(t, v)) = \lambda(s, t)\)。
所以这下算法过程也就很明晰了:还是使用分治法。每次随意选出两个点 \(s, t\) 求出最小割,然后根据 \(\alpha(s, t)\) 将图划分为两个部分。对于 \(s\) 侧,我们需要将 \(t\) 侧缩为一个点(避免接下来的分治过程中将 \(t\) 侧割开了),然后再往下分治;对于 \(t\) 侧同理。回溯时,按照条件 1 取出合适的 \(u, v\),然后相连(这里需要注意的是,不要取出缩成的点,要取原图中的点)。
代码(你可以在 @Eznibuil 大佬的 U278541 【模板】Gomory-Hu 处测试你算法的正确性):
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 505, MAXM = 1505, INF = 0x3f3f3f3f;
int n, m, q, e = 1, s, t, tot, head[MAXN], c[MAXN<<1];
vector<int> vec[MAXN<<1];
stack<int> nm[MAXN];
struct node{
int to, nxt, ci;
} edge1[MAXM<<2], edge2[MAXM<<2];
inline void Add_Edge(int u, int v, int c){
edge1[++e] = {v, head[u], c}, head[u] = e;
edge1[++e] = {u, head[v], 0}, head[v] = e;
return;
}
//-----
int d[MAXN<<1], now[MAXN];
inline bool BFS(){
for(int i = 1; i <= n; i++) now[i] = head[i];
for(int i = 1; i <= tot; i++) d[i] = 0;
queue<int> que;
que.push(s); d[s] = 1;
while(!que.empty()){
int qwq = que.front(); que.pop();
for(int x : vec[qwq])
for(int i = head[x]; i; i = edge2[i].nxt){
int to = nm[edge2[i].to].top();
if(d[to] or !edge2[i].ci) continue;
d[to] = d[qwq]+1;
que.push(to);
if(to == t) return true;
}
}
return false;
}
inline int DFS(int qwq, int flow){
if(qwq == t) return flow;
int rest = flow;
for(int x : vec[qwq])
for(int i = now[x]; i and rest; i = edge2[i].nxt){
int to = nm[edge2[i].to].top();
now[x] = i;
if(!edge2[i].ci) continue;
if(d[to] != d[qwq]+1) continue;
int tmp = DFS(to, min(rest, edge2[i].ci));
if(!tmp) d[to] = 0;
rest -= tmp, edge2[i].ci -= tmp, edge2[i^1].ci += tmp;
}
return flow-rest;
}
inline int Dinic(int x, int y){
s = x, t = y;
for(int i = 1; i <= e; i++) edge2[i] = edge1[i];
for(int i = 1; i <= n; i++) vec[nm[i].top()].push_back(i);//vec 储存缩出的这个点里有哪些原图的点。
int maxflow = 0;
while(BFS()) maxflow += DFS(s, INF);
for(int i = 1; i <= tot; i++) vec[i].clear();
return maxflow;
}
//-----
inline void Div(int x){
int y = -1;
for(int i = 1; i <= n; i++) if(i != x and nm[i].top() == i) y = i;
if(y == -1){
for(int i = 1; i <= n; i++) if(i != x) c[nm[i].top()] = x;//标记一直到分治终止时 x 没有与这些连通块割开。
return;
}
int w = Dinic(x, y);
++tot;
for(int i = 1; i <= n; i++){
int tmp = nm[i].top();//nm[i].top() 表示当前点 i 被缩了到哪个连通块里。写成栈是为了方便回溯。
if(d[tmp]) nm[i].push(tot), nm[i].push(tmp);
else nm[i].push(tmp), nm[i].push(tot);
}
Div(x); int u = c[tot];
for(int i = 1; i <= n; i++) nm[i].pop();
Div(y); int v = c[tot];
for(int i = 1; i <= n; i++) nm[i].pop();
--tot;
printf("%d %d %d\n", u, v, w);
return;
}
//-----
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
int u, v, w; scanf("%d%d%d", &u, &v, &w);
Add_Edge(u, v, w), Add_Edge(v, u, w);
}
for(int i = 1; i <= n; i++) nm[i].push(i);
tot = n;
Div(1);
return 0;
}
时间复杂度:\(O(n^3m)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号