再探HashMap

目录

• 一、底层原理
  • • 1、哈希算法
    • 2、哈希冲突
• 二、手写HashMap——数组+链表
  • • 1、Map接口
    • 2、HashMap类

一、底层原理

1、哈希算法

哈希算法（也叫散列算法），就是把任意长度值（key）通过哈希算法变换成固定长度的key（地址），通过这个地址进行访问的数据结构

通过把关键码值映射到表中的一个位置来访问记录，以加快查找的速度

具有幂等性，即指的是多次操作，结果是一致的

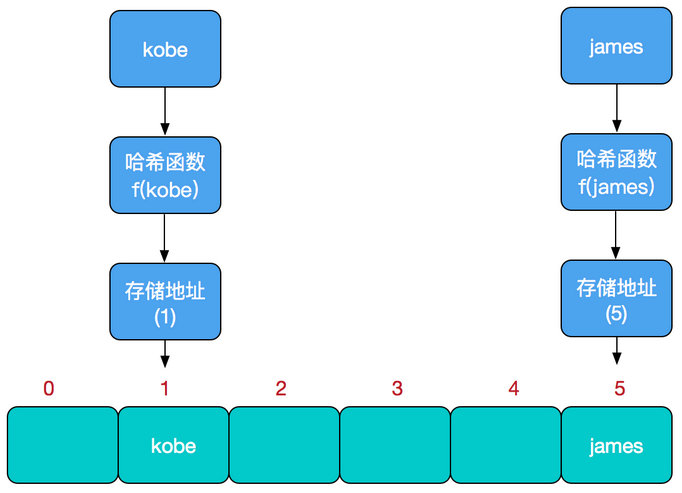
流程：

• 算出字符串的ascii码
• 进行mod（取模）
  • 为什么要取模？
    如果以算出的字符串对应的ascii码来找到对应的下标，会导致需要使用很大的空间来存储数组
• 算出哈希表的下标

2、哈希冲突

两个不同的元素，通过哈希函数的计算得出了相同的实际存储地址，这就是哈希冲突

解决方法：

• 开放寻址法：发生冲突，继续寻找下一块未被占用的地址
• 拉链法：数组+链表——可以理解为链表的数组

当通过哈希函数计算得到的地址被占用，将新元素以链表的形式放在老元素的后面，则此时的Entry中还有一个执行后一元素的next指针

二、手写HashMap——数组+链表

1、Map接口

public interface Map<K, V> {

    V put(K k, V v);
    V get(K k);
    int size();

    interface Entry<K, V> {
        K getKey();
        V getValue();
    }
}

2、HashMap类

public class HashMap_<K, V> implements Map<K, V> {

    Entry<K, V>[] table = null;
    int size = 0;

    public HashMap_() {
        table = new Entry[16];
    }

    class Entry<K, V> implements Map.Entry<K, V> {
        K k;
        V v;
        int index;
        Entry<K, V> next;

        public Entry(K k, V v, int index, Entry<K, V> next) {
            this.k = k;
            this.v = v;
            this.index = index;
            this.next = next;
        }

        @Override
        public K getKey() {
            return k;
        }

        @Override
        public V getValue() {
            return v;
        }
    }

    /**
     * 1、put方法
     * （1）key进行hash，取模算出index下标
     * （2）数组对应的节点对象是否为空
     * （3）为空，赋值存储
     * （4）不为空，冲突，链表存储
     * （5）返回值
     */
    @Override
    public V put(K k, V v) {
        int index = hash(k);
        Entry<K, V> entry = table[index];
        if (entry == null) {//没有冲突
            table[index] = new Entry<>(k, v, index, null);
            size++;
        } else {//有冲突
            table[index] = new Entry<>(k, v, index, entry);//此时的entry指向的就是该索引处的节点，next——>entry
        }

        return table[index].getValue();
    }

    private int hash(K k) {
        int index = k.hashCode() % 16;
        return index >= 0 ? index : -index;//防止为负数
    }

    /**
     * 2、get方法
     * （1）key进行hash，取模算出index下标
     * （2）数组对应的节点对象是否为空
     * （3）为空，直接返回null
     * （4）不为空，比较key值，判断对象是否相等
     * （5）如果相等，返回数据
     * （6）如果不相等，next是否为空
     * （7）为空，直接返回null
     * （8）不为空，判断下一个节点，查询k与节点key是否相等
     * （9）直到相等为止
     */
    @Override
    public V get(K k) {
        int index = hash(k);
        Entry<K, V> entry = findValue(table[index], k);

        return entry == null ? null : entry.getValue();
    }

    public Entry<K, V> findValue(Entry<K, V> entry, K k) {
        if (k.equals(entry.getKey()) || k == entry.getKey()) {
            return entry;
        } else {
            if (entry.next != null) {
                return findValue(entry.next, k);//递归查询链表下一个节点
            }
            return null;
        }
    }

    @Override
    public int size() {
        return size;
    }
}