<leetcode c++>685. 冗余连接 II

685. 冗余连接 II

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

 

示例 1：

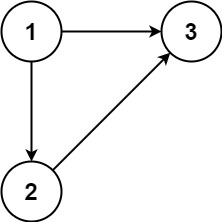
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

示例 2：

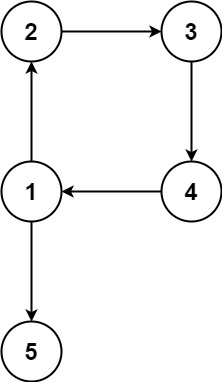
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

 

提示：

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ui, vi <= n

 

 一颗树加入一条冗余边后共有三种可能产生的情况：

1. 只有环——输出形成环的最后一条边
2. 只有冲突边——输出冲突的那条边
3. 有环有冲突——输出 冲突边中的孩子 与在 环中该孩子的那个父亲结点 形成的那条边

 

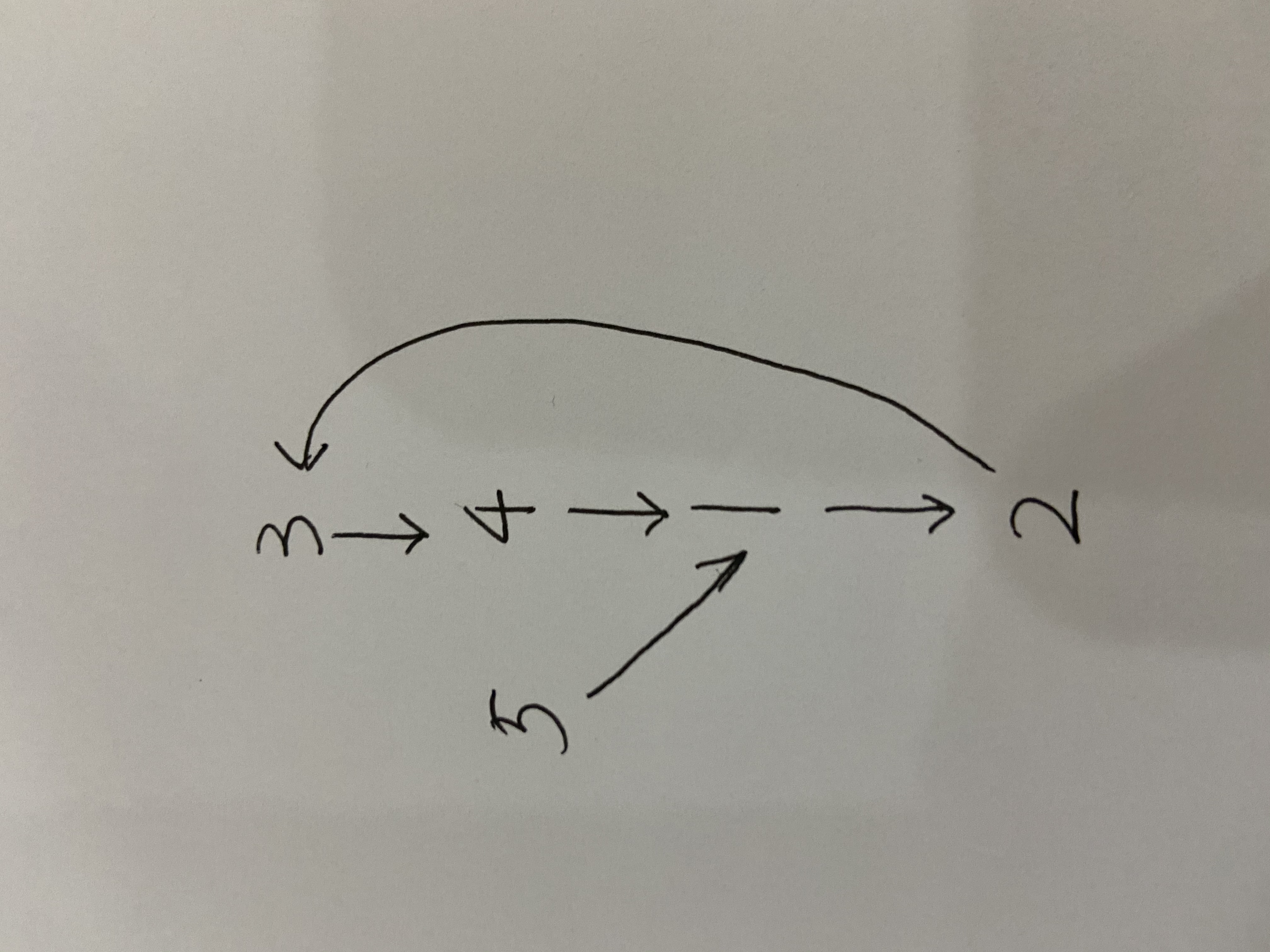
 对于第三点，因为存在环只需要解除环中的任意一条边， 而解决冲突只需解决两条冲突边中的一条，取二者交集就是所说情况，如下图示意：

边[5, 1] 与 边[4, 1]冲突， 而[4, 1] 又在环中， 所以我们输出冗余边[4, 1] 

 

 代码如下：

class Solution {
public:
    //并查集
    vector<int> parent;
    int find(int x){
        if(x != parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }
    void un(int x, int y){
        parent[find(y)] = find(x);
    }
    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        parent = vector<int>(n + 1, 0);
        iota(parent.begin(), parent.end(), 0);
        vector<int> ancester(n + 1, 0);
        int conflict = -1;
        int cycle = -1;
        for(int i = 0; i < n; i++){
            int u = edges[i][0], v = edges[i][1];
            if(find(v) != v){
                conflict = i;
            }else{
                ancester[v] = u;
                if(find(v) == find(u)){
                    cycle = i;
                }else
                    un(u, v);
            }
        }
        if(conflict > 0){
            if(cycle < 0){
                return vector<int>({edges[conflict][0],edges[conflict][1]});
            }else{
                return vector<int>({ancester[edges[conflict][1]], edges[conflict][1]});
            }
        }
        return vector<int>({edges[cycle][0], edges[cycle][1]});
    }
};