2.3 性能度量
ROC和RUC
学习器为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值进行比较,若大于阈值则分为正类,否则分为反类;
ROC(受试者工作特征 横轴-真正例率(TPR) 纵轴-假正例率(FPR))
TPR=TP/(TP+FN) FPR=FP/(TN + FP);
绘图过程:
给定m+个正例和m-个反例,根据学习器的预测结果对样例进行排序,然后把分类阈值设为最大,即把所有样例均预测为反例;
若为真正例,则上移1/m+单位;
若为假正例,则右移1/m-单位。
这样恰恰说明了为什么横轴就表示FPR,纵轴就表示TPR。
经过(m+ add m-)次的猜测,就得到从(0,0)到(1,1)的折线ROC。
对每个点作关于x,y轴的直线,将该区域分成 m+ mulpitly m- 块小矩形。
在ROC曲线之下的面积是AUC(Area Under ROC Curve)
经过(m+ add m-)次的猜测,就得到从(0,0)到(1,1)的折线ROC。
对每个点作关于x,y轴的直线,将该区域分成 m+ mulpitly m- 块小矩形。
,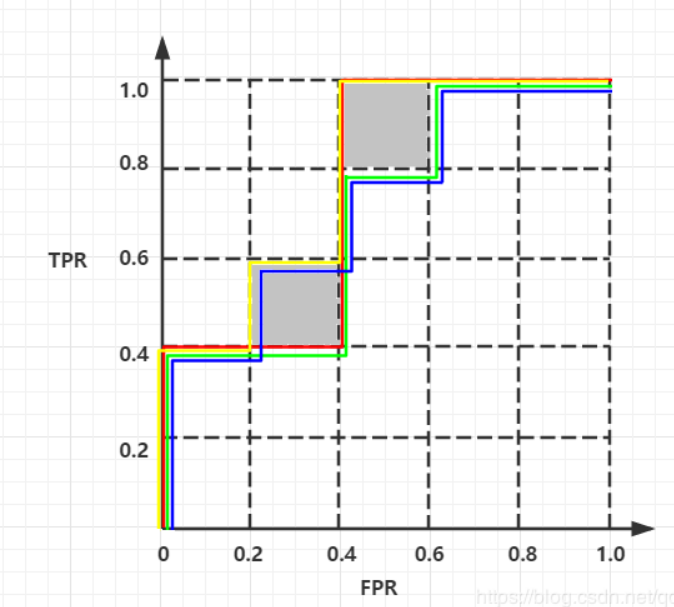
思考:对于不同的排序而言会产生灰色区域的误差;因此需要考虑f(x+)=f(x-)的误差;
ROC曲线上方的面积等于m-块底为1/m-,高为1/m+ multiple (剩余的正例数目),并考虑排序带来的影响
故 得到书上的损失公式。
2.3.4代价敏感错误率和代价曲线
为了衡量不同类型错误所造成的不同损失,可以赋予“非均等代价” 对于代价而言,重要的是代价比值而不是代价绝对值
在非均等代价下,ROC曲线不能直接反映出 学习器的期望总体代价,而“代价曲线”可以达到目的;
costij表示将第i类样本预测为第j类样本的代价,若预测正确则代价为0,设置代价矩阵如下:
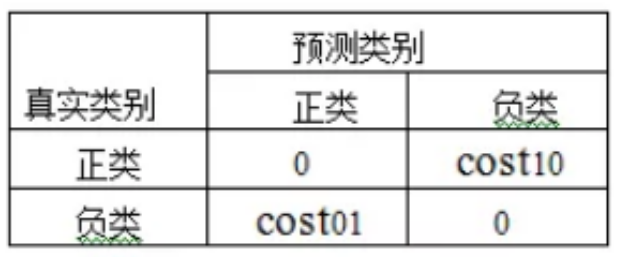
因此模型代价敏感错误率为:
不管使用何种代价损失函数,构建模型最优化都等价与最小代价敏感错误率
代价曲线:期望总体代价越小,则模型的泛化能力越强;
代价曲线的横坐标是样例为归一化的正例概率代价,正例概率为p,给定的正例概率为先验概率,范围为0~1,纵轴是归一化的损失代价。
归一化的正例代价概率为: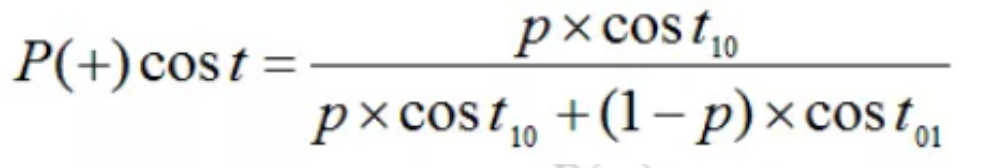
这里 用1代表正样本,0代表负样本; (西瓜书里面假设0代表正例,1代表反例)
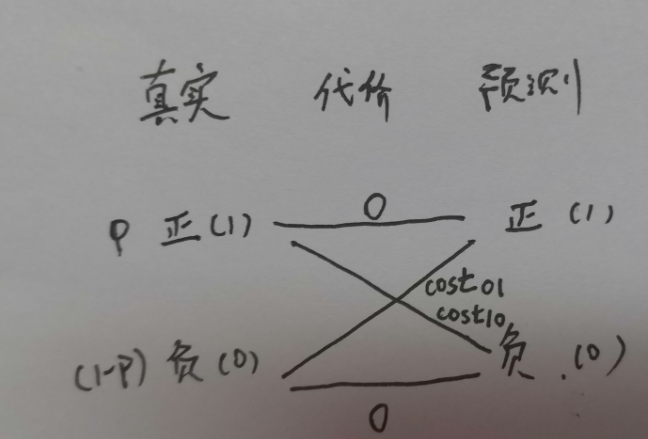
正概率代价为![]()
总概率代价为: 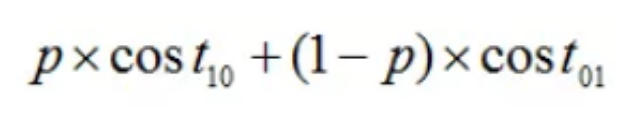




 浙公网安备 33010602011771号
浙公网安备 33010602011771号