智能机器人复习总结
3月14号更新
7道答题:
- 写齐次坐标变换矩阵和四元数
- 边缘检测:灰度、一阶、二阶
- 小孔成像,逆过程硬核计算
- SLAM线程,后端优化算法,回环检测目的,词袋
- 地图种类,A*算法流程,实际地图求解
- 机器人全局运动到局部运动计算,解释
- PID离散表达式,PID算法,原理,控制曲线,ROS控制器相关
机器人三原则
- 机器人必须不危害人类,也不允许它眼看人将受害而袖手旁观;
- 机器人必须绝对服从于人类,除非这种服从有害于人类;
- 机器人必须保护自身不受伤害,除非为了保护人类或者是人类命令它作出牺牲。
机器人典型架构
以可佳为例:
- 环境感知:建图、定位、SLAM、避障
- 自主行动:导航、路径规划,运动规划,避障
- 人-机器人交互:自然语言处理,对话管理
- 系统集成:机器人操作系统,ROS
- 以上硬件支持:电机,传感器(语音、视觉、激光、声呐)
空间坐标
基本概念
- 世界坐标系:定义的最大坐标系
- 模型坐标系:建立在特定物体上,用于描述该物体前后左右关系
- 摄像机坐标系:是和观察者密切相关的坐标系,该坐标系定义在摄像机的屏幕可视区域
- 齐次坐标概念
旋转矩阵和平移向量
将齐次矩阵作为变换矩阵,乘以一点在MC中的坐标,得到该点WC中坐标,其中旋转是绕旋转轴逆时针旋转
\(T\)表示MC相对于WC的平移向量,\(R\)表示MC相对于WC的旋转矩阵。\(x\)是MC中的坐标,\(x^{'}\)是WC中的坐标。
旋转向量
任意旋转都可以用一个旋转轴和一个旋转角来刻画。
于是,我们可以使用一个旋转向量,其方向与旋转轴一致,而长度等于旋转角。
欧拉角
把任意旋转分解成以下三个轴上的转角:
- 绕物体的 Z 轴旋转,得到偏航角 yaw;
- 绕旋转之后的 Y 轴旋转,得到俯仰角 pitch;
- 绕旋转之后的 X 轴旋转,得到滚转角 roll。
此时,我们可以使用 \(\left[r, p , y\right]^{T}\) 这样一个三维的列向量描述任意旋转。
四元数
假设某个旋转是绕单位向量 \(\boldsymbol{n}=\left[n_{x}, n_{y} , n_{z}\right]^{T}\)进行了角度为 θ 的旋转,那么这个旋转的四元数形式为:
视觉系统
-
小孔成像模型
投影顺序:世界坐标—R,t—>相机坐标—z=1,三维变二维—>归一化平面—内参—>像素坐标

-
色彩空间
RGB色彩空间、HSV色彩空间:色相、明度、饱和度 -
图像的边缘
像素亮度显著变化的地方:一阶差分极大值,二阶差分过零点
-
直方图
直方图均衡化:提高对比度
灰度尺度变换,使白的更白,黑的更黑。 -
滤波器:去除噪声
-
椒盐噪声、脉冲噪声、高斯噪声
-
线性滤波器:均值滤波器(可能导致边缘模糊)、高斯平滑滤波器
-
非线性滤波器:中值滤波器(可以去除脉冲噪声、椒盐噪声同时保留图像边缘细节)、边缘保持滤波器
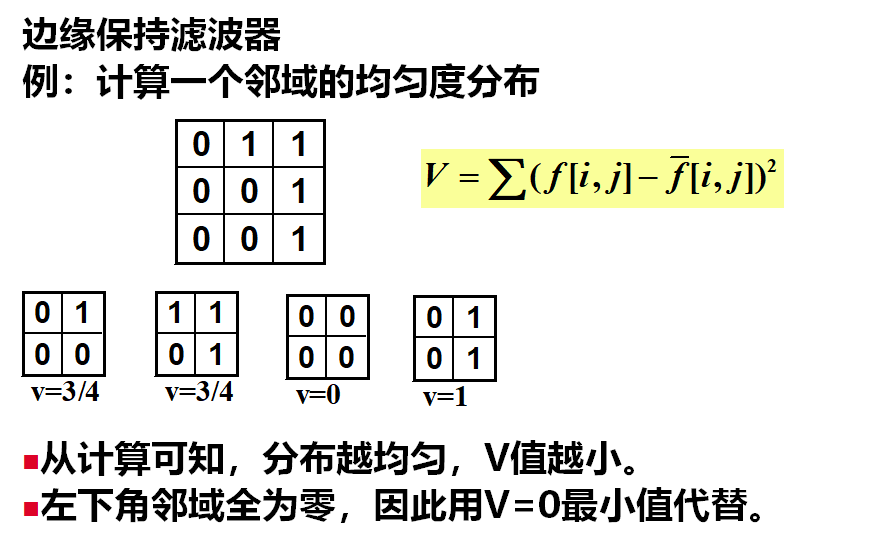
-
-
卷积运算是指从图像的左上角开始,开一个与模板同样大小的活动窗口,窗口图像与模板像元对应起来相乘再相加,并用计算结果代替窗口中心的像元亮度值。然后,活动窗口向右移动一列,并作同样的运算。以此类推,从左到右、从上到下,即可得到一幅新图像。
边缘检测
- 一阶边缘检测算子
Sobel:
其中\(G_{x}\)检测竖直边缘, \(G_{y}\)检测横向边缘
同理有Prewitt算子
-
二阶边缘检测算子
拉普拉斯算子:\[\left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right] \]
-
二阶边缘检测算法
canny算法流程:- 用高斯平滑滤波器平滑图像
- 用一阶偏导数的有限差分来计算图像的梯度的幅度和方向(可采用一阶边缘检测算法)
- 对梯度幅度值进行非极大值抑制(对边缘进行瘦身)
- 用双阈值算法检测和连接边缘
-
链码表示边缘
一阶差分链码:差分链码具有旋转不变性,可用于手写体识别 -
二值图像
膨胀:消除图像中无用的点
腐蚀:增加相应像素
视觉里程计
图像深度获取
- 散焦深度法
- RGB-D相机模型
- 双目相机法
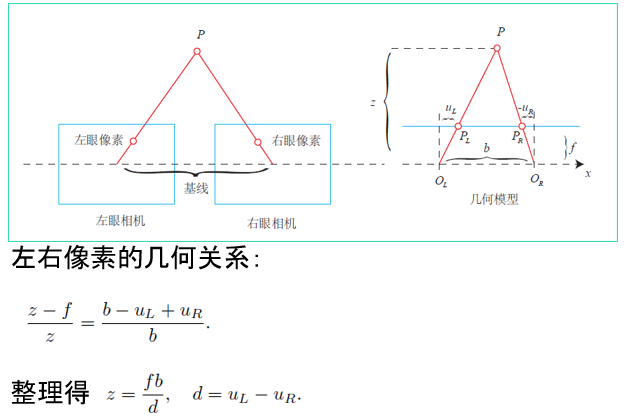
特征点法视觉里程计
特征点由关键点(位置、大小、方向、评分等)和描述子(特征点周围的图像信息)构成
FAST角点:只检查关键点
ORB角点:slam选用
双目相机特征点法视觉里程计工作流程
Input:左右图像、前后图像序列、左右相机的内参、外参
- 获得左右图像、图像校正
- 提取图像特征点
- 左右图像特征匹配,获取特征点坐标
- 前后图像特征匹配
- 增量式的运动估计
- 2D-2D:对极几何
- 3D-2D:PnP
- 3D-3D:ICP
Output:图像对之间的位姿关系、相机轨迹等
光流法视觉里程计
保留特征点,只计算关键点,使用光流法跟踪特征点的运动,避免计算和匹配描述子带来的时间
- 亮度恒定,就是同一点随着时间的变化,其亮度不会发生改变
- 小运动,这个必须满足,就是时间的变化不会引起位置的剧烈变化
光流法视觉里程计流程:
- 图像获取:单目照相机、双目照相机或者全向照相机;
- 图像校正:使用一些图像处理技术来去除透镜畸变;
- 特征检测:确定感兴趣的描述符,在帧与帧之间匹配特征并构建光流场;
- 检查光流场向量是否存在潜在的跟踪误差,移除外点;
- 由光流场估计照相机的运动;
- 可使用卡尔曼滤波进行状态估计
- 2D-2D等
- 周期性的重定位跟踪点。
学会求解超定方程即可,求解出的\(x_{1},x_{2}\)即为照相机在\(x,y\)方向的移动距离。



变型:直接法视觉里程计
只计算关键点,不计算描述子,使用直接法计算特征点在下一帧画面的位置
SLAM框架
视觉slam流程(框架):
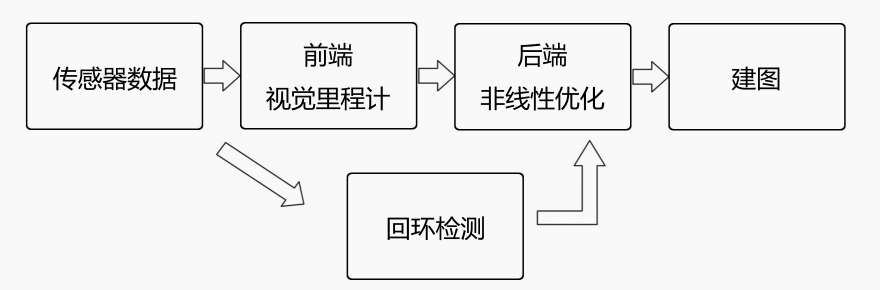
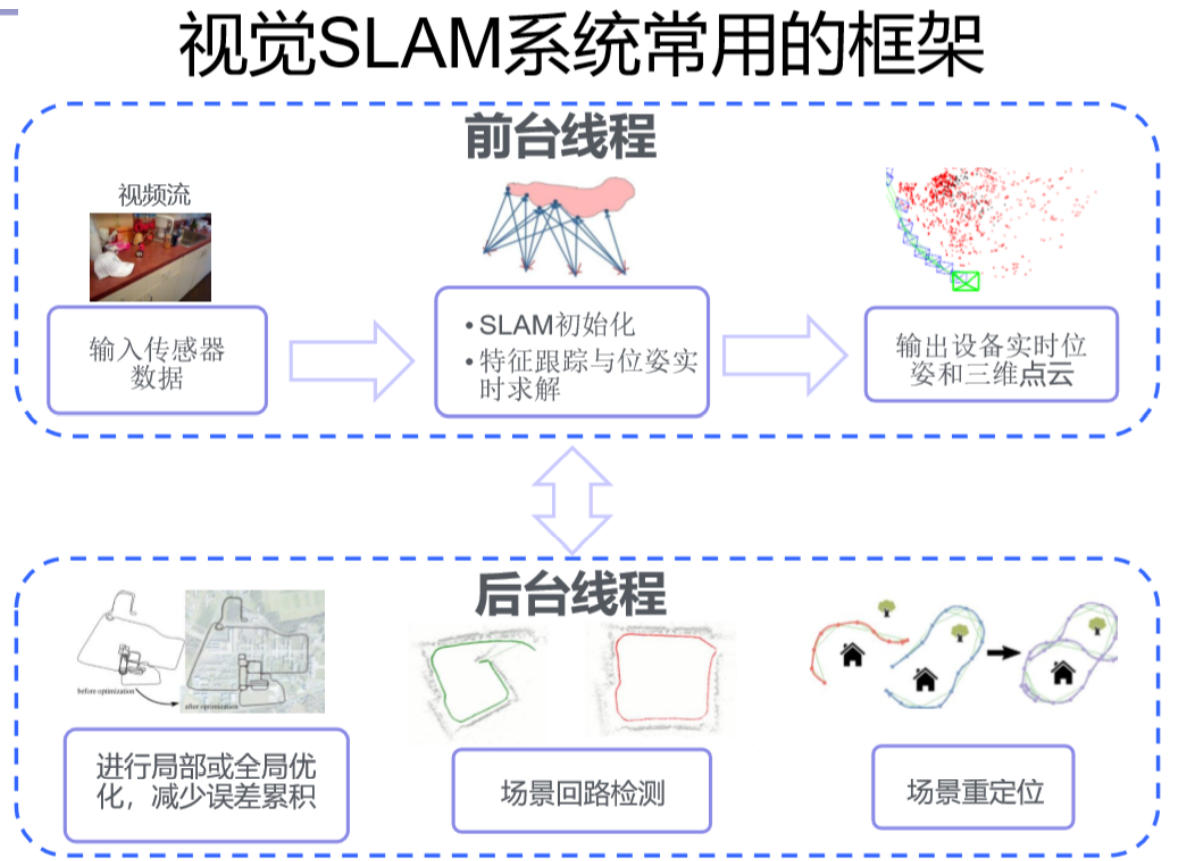
-
传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。
-
视觉里程计。视觉里程计任务是估算相邻图像间相机的运动,以及局部地图的样子。VO 又称为前端。
-
后端优化。后端接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图。由于接在 VO 之后,又称为后端。重定位、回路闭合、稠密三维恢复(状态估计和非线性优化)
-
回环检测。回环检测判断机器人是否曾经到达过先前的位置。如果检测到回环,它会把信息提供给后端进行处理。(解决随时间漂移问题)
-
建图。它根据估计的轨迹,建立与任务要求对应的地图。
线性高斯系统是最简单的,它的无偏的最优估计可以由卡尔曼滤波器给出。
卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。
路径规划
Dijkstra算法
Dijkstra算法运行得较慢,但确实能保证找到一条最短路径。
最佳优先搜索(BFS)算法
BFS能够评估任意结点到目标点的代价,它选择离目标最近的结点。
例如,如果目标位于出发点的南方,BFS将趋向于导向南方的路径。在下面的图中,越黄的结点代表越高的启发式值(移动到目标的代价高),而越黑的结点代表越低的启发式值(移动到目标的代价低)。
BFS运行得较快,但是它找到的路径明显不是一条好的路径
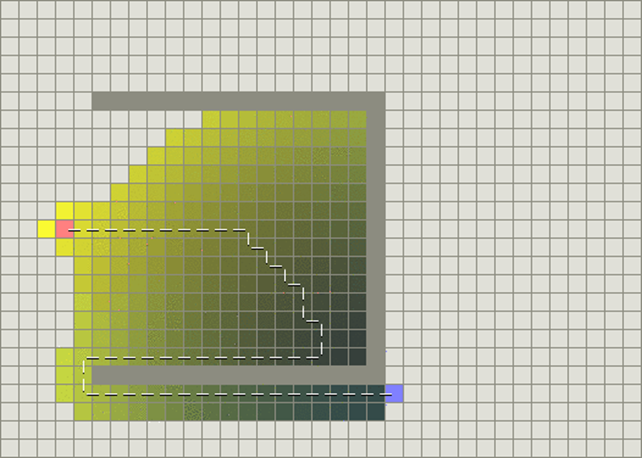
A*算法 = Dijkstra + BFS 算法
其中g(n)表示从初始结点到任意结点n的代价,h(n)表示从结点n到目标点的启发式评估代价
即:
g(n) = 从起点 A 移动到指定方格的移动代价,沿着到达该方格而生成的路径。
h(n) = 从指定的方格移动到终点 B 的估算成本。
算法步骤:
-
从节点A开始,把一系列待考虑的节点放入OpenList里面,OpenList存放着一系列需要检查的节点(方块),如图,首先检查起点周围的8个节点。
代码实现思想:
- 有两个集合,OPEN集和CLOSED集,其中OPEN集保存待考查的结点,开始时,OPEN集只包含一个元素:初始结点。CLOSED集保存已考查过的结点,开始时,CLOSED集是空的。
- 在主循环中重复地从OPEN集中取出最好的结点n(f值最小的结点)并检查之。如果n是目标结点,则我们的任务完成了。否则,结点n被从OPEN集中删除并加入CLOSED集 。
-
找到 f 值最小的节点作为新的起点
- 将它从OpenLsit中删除,加入到ClosedList里面
- 检查它的临近节点,忽略已经在ClosedList中的节点和不可行节点(障碍)
- 如果临近节点已经在OpenList里面,则对比一下是否从现节点到临近节点的G值比原G值小,若是,把现节点作为父节点。否,不做改动
-
上步骤中新节点未造成任何改动,我们继续在OpenList中寻找新的节点。重复1),2)中的步骤,直到找到目标节点。
A*算法[1]在运算过程中,每次从优先队列中选取f(n)值最小(优先级最高)的节点作为下一个待遍历的节点。
另外,A*算法使用两个集合来表示待遍历的节点,与已经遍历过的节点,这通常称之为open_set和close_set。
* 初始化open_set和close_set;
* 将起点加入open_set中,并设置优先级为0(优先级最高);
* 如果open_set不为空,则从open_set中选取优先级最高的节点n:
* 如果节点n为终点,则:
* 从终点开始逐步追踪parent节点,一直达到起点;
* 返回找到的结果路径,算法结束;
* 如果节点n不是终点,则:
* 将节点n从open_set中删除,并加入close_set中;
* 遍历节点n所有的邻近节点:
* 如果邻近节点m在close_set中或障碍物,则:
* 跳过,选取下一个邻近节点
* 如果邻近节点m也不在open_set中,则:
* 计算节点m的优先级
* 根据优先级判断是否需要更新节点m的parent为节点n
* 将节点m加入open_set中
D*算法
Dynamic A,应用于在动态环境下的搜索,动态路径最短路是外界环境不断发生变化,即不能计算预测的情况下计算最短路径。
D只检查上下一节点或邻近节点的变化情况,当下一节点没有变化时,无需计算,利用上一步Dijstra计算出的最短路信息从出发点向后追述即可。
避障
- BUG法:绕着障碍物外围一圈或半圈避障。
- 人工势场法:类似于等高线。
- 向量场直方图
机器人的移动性设计
运动方式:足式、轮式
足式:
- 足的规模,数目越少,运动模式越复杂
- 稳定性, 静态稳定至少需要三条腿
- 每条腿的关节数:多数情形下每条腿需要三个自由度
轮式:
- 3个轮子静态稳定性
- 更多轮子动态稳定性/悬挂
机器人运动学
全局坐标到局部坐标的映射关系:
该映射可由(绕z轴)正交旋转矩阵来表示,得到的结果是局部坐标系的运动结果。
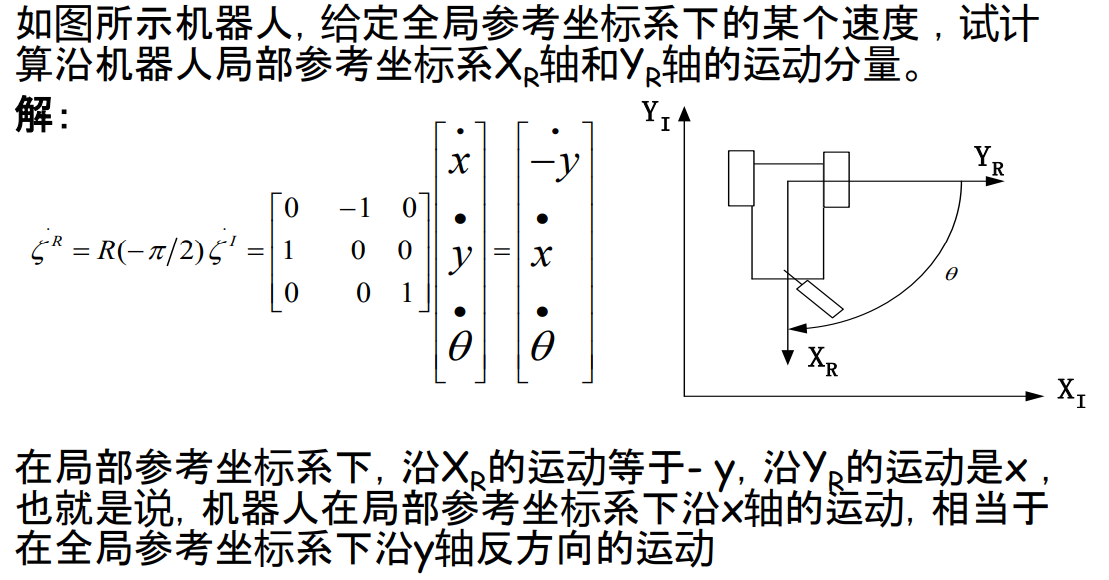
滚轮到全局
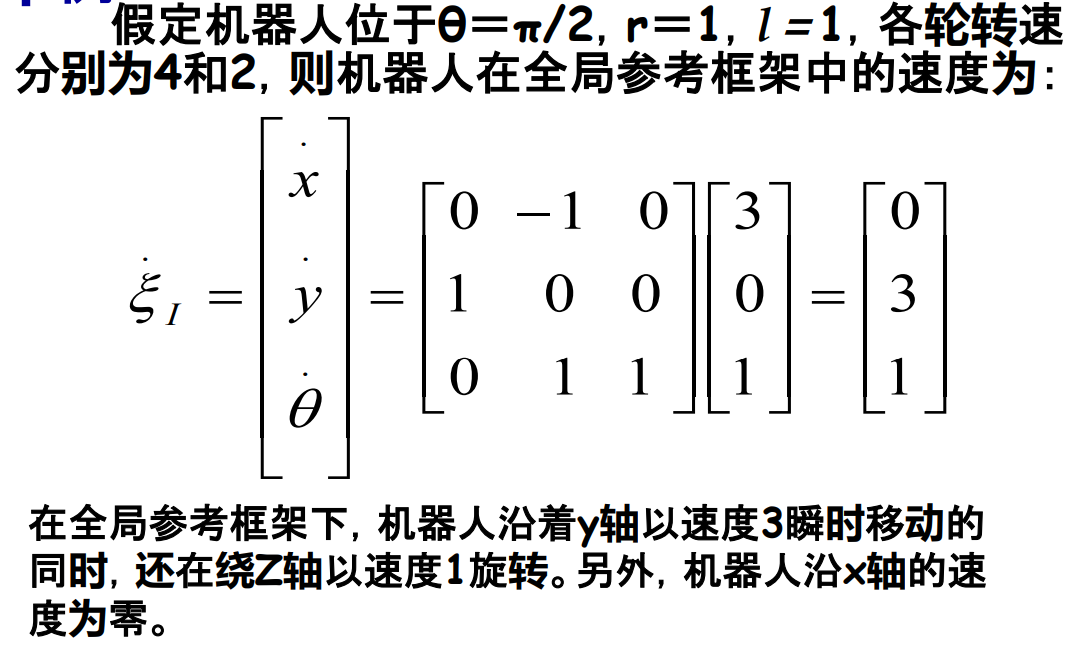
\({\xi}_{I}\)表示全局运动, \({\varphi}\)表示转速。
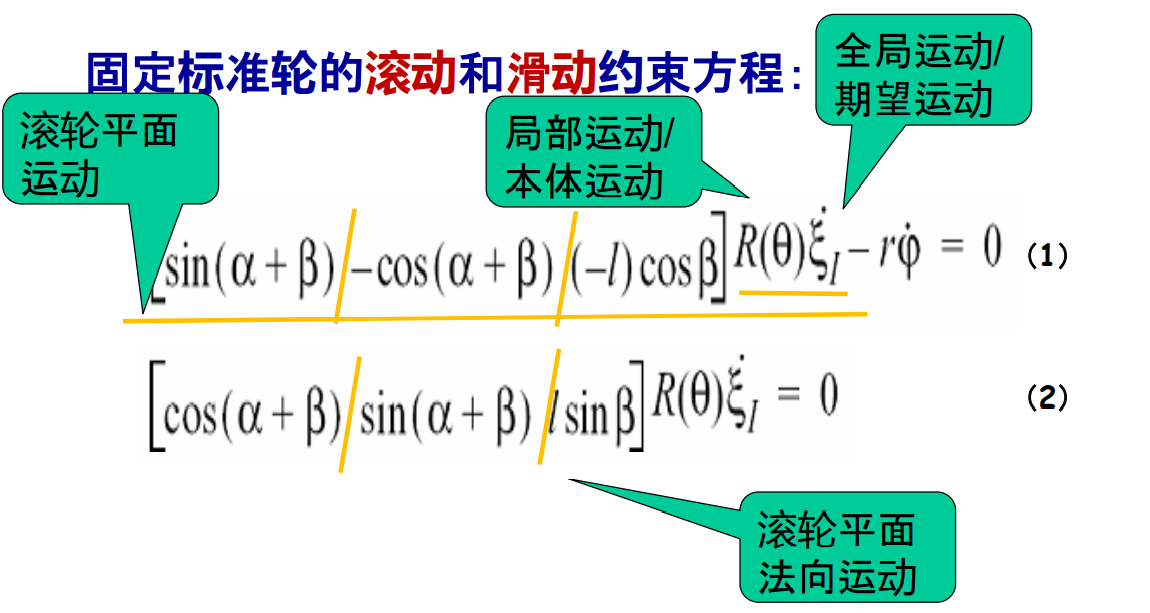
固定轮约束方程
全局参考框架下的运动变换到机器人局部参考框架内的运动,注意\(R(\theta)\)
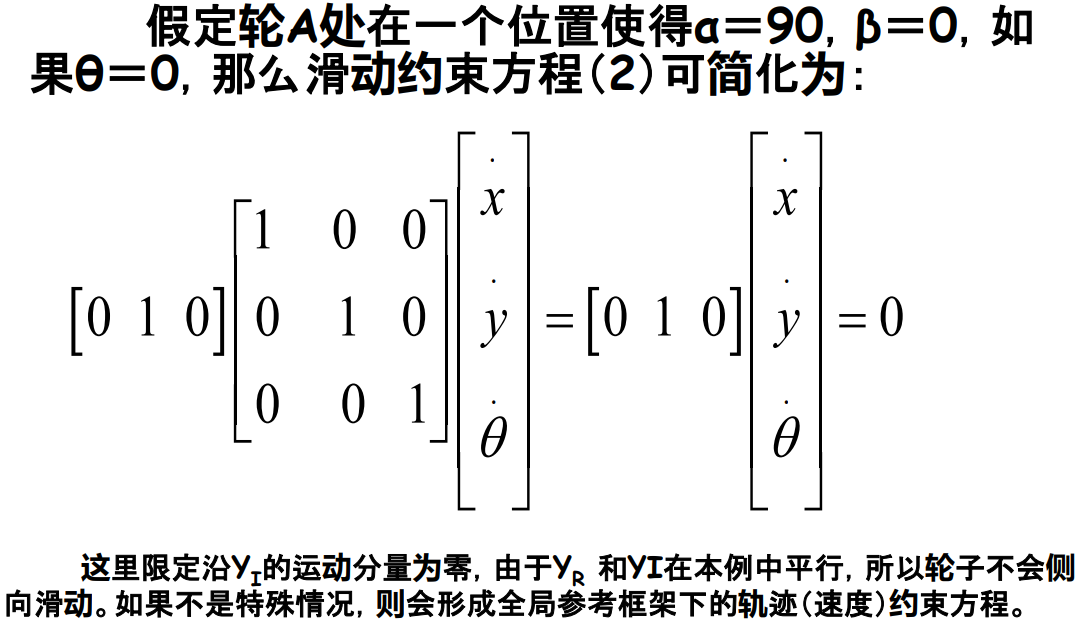 )
)
PID控制理论
系统偏差的比例(Proportional)、积分(Integral)和微分(Derivative)的综合控制,简称PID控制,可以想象淋浴调水温。
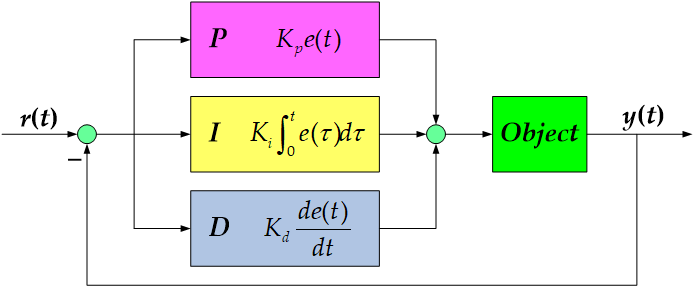
在连续系统中,其关系式为:
PID控制器的Kp,Ti,Td三个参数的大小决定了PID控制器的比例、积分、微分控制作用的强弱。
PID控制器中三个环节的作用总结:
-
比例环节的作用:成比例地反映控制系统的偏差信号,偏差一旦产生,立即产生控制作用以减小偏差。比例控制器的输出u(t)与输入偏差e(t)成正比,能迅速反映偏差,从而减小偏差,但不能消除静差。静差是指系统控制过程趋于稳定时,给定值与输出量的实测值之差。
-
积分环节的作用:主要用于消除静差提高系统的无差度。积分作用的强弱,取决于积分时间常数Ti,Ti越大积分作用越弱,反之则越强。积分作用太强会使系统超调加大,甚至使系统出现振荡。
-
微分环节的作用:有助于系统减小超调,克服振荡,加快系统的响应速度,减小调节时间,从而改善了系统的动态性能。但Td过大,会使系统出现不稳定。
PID控制参数调整步骤:先比例,后积分,再微分。
PID算法种类:位置式控制算法、增量式控制算法
代码实现:
/**
* 数据类型:@float
* Set_Value:设置值(期望值)
* Current_Value:实际值(反馈值)
* Error:当前误差
* LastError:前一次误差
* LastError2:再前一次误差
*/
// 增量式PID
Error=Set_Value - Current_Value;
result= p * (Error - LastError)
+ i * Error
+ d * (Error - 2*LastError + LastError2);
LastError2 = LastError;
LastError = Error;
return result;
// 位置式PID
Error=Set_Value - Current_Value;
SumError += Error;
dError = LastError - LastError2;
LastError2 = LastError;
LastError = Error;
result= p * Error
+ i * SumError
+ d * dError;
return result;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号