CF1991D — Prime XOR Coloring

---

蛤？什么奇奇怪怪奇技淫巧

---

诸君请看题：

诸君请看样例：

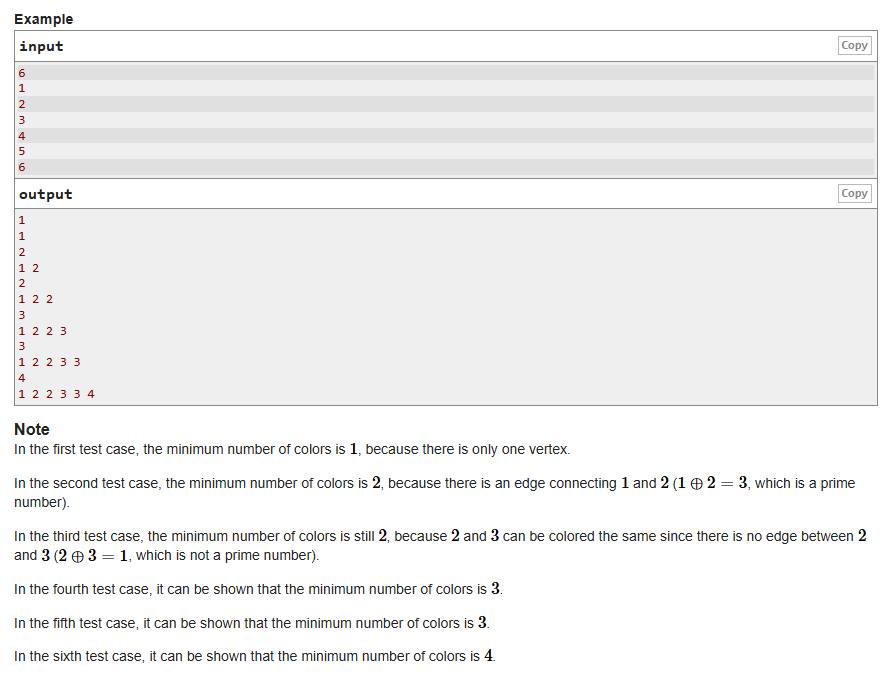
嗯？怎么没有大样例呢？

嗯？为什么还要输出方案呢？

嗯？为什么要这么麻烦呢？

---

诸君请看代码：

嗯？什么奇奇怪怪的打表

---

原来是诈骗题啊！原来是诈骗题啊！原来是trash题啊！

原来ans=4啊！！！原来方案就是%4+1啊！！！

---

总结一下我们的做法吧~

类二分图+孪生素数学说

首先抑或和纸鼠是没有什么关系的，近似随机了吧~

关系就是，偶数除2都不是纸鼠，抑或看末位发现，11–>0，00–>0，也就是奇数奇数和偶数偶数抑或起来都是偶数

根据这个性质我们可以奇偶分两个集合，同一个集合无边，中间一坨乱七八糟的边

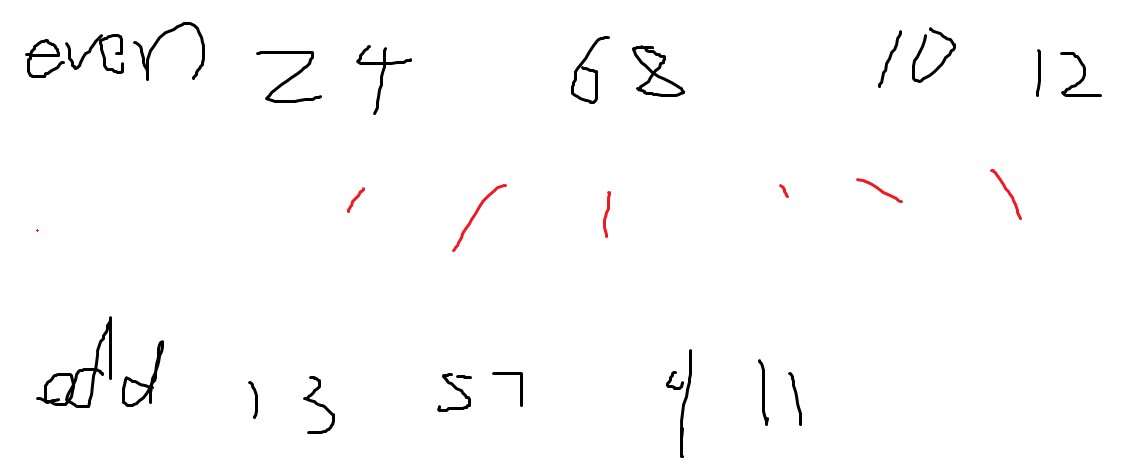
什么奇奇怪怪的美图

但是2是一个特例，同一个集合里如果抑或是2也有边，也就是x与x^2之间

考虑到这个我们可以将x与x^2组队，看成一个点，来讨论内部关系，同时对于外部也不破坏二分图的性质

然后我们可以看到任意两个组队后的点，设为(x,x^2)和(y,y^2)，不同集合里面的，然后我们来讨论x^y

我们可以看到，这四个点里面的边就是(x^y),(x^y^2),(x^2^y),(x^2^y^2)

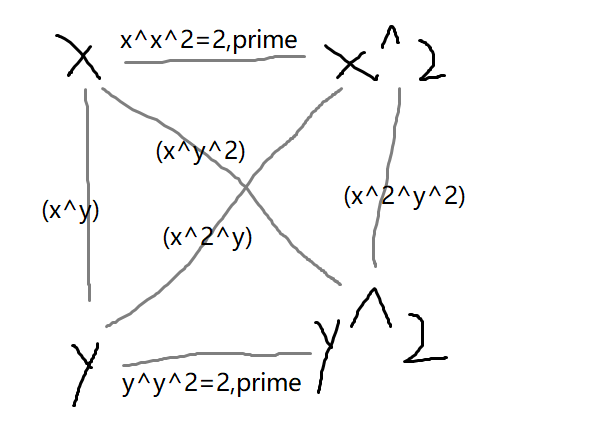
相当于就是(x^y),(x^y^2)这俩

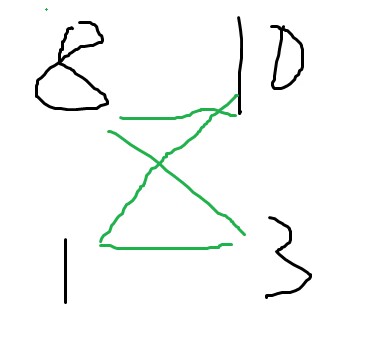
然后他们可能都不是纸鼠，那就啥都没有不用管

也有可能只有一个是纸鼠，那样的话是纸鼠的那两条边就都存在，就是这种绿色的沙漏（但是也可以两条边直着连吧，如果前者是后者不是的话）

也有可能是“孪生素数”，就是四条边都有，红色情况

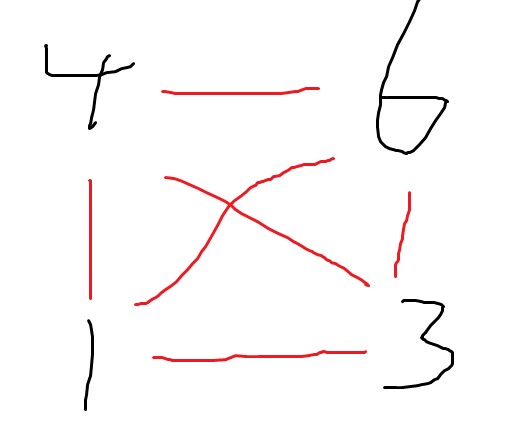
孪生素数指x^y和x^y^2都是质数哦~（^2就是+-2的成对变换）

化完简，里面就分红绿两种情况，外面还是二分图

因为这时候同一个集合里是无边的，所以根据二分图他的染色性质，俩颜色一黑一白就可以搞定

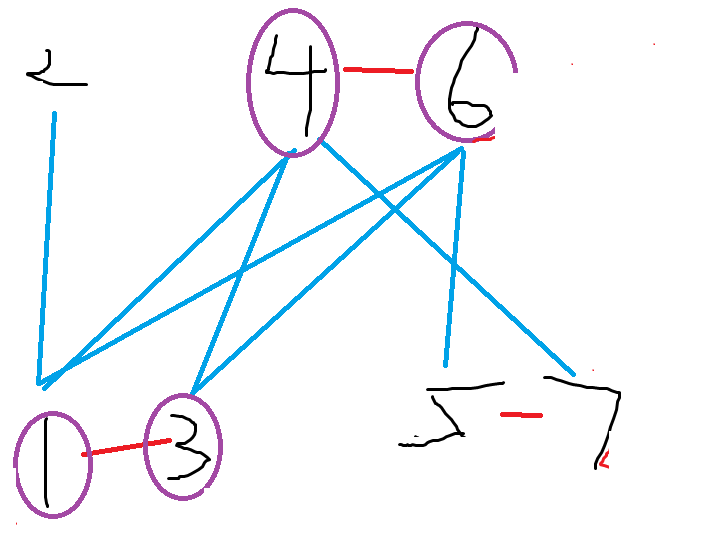
这是1-7的具体情况

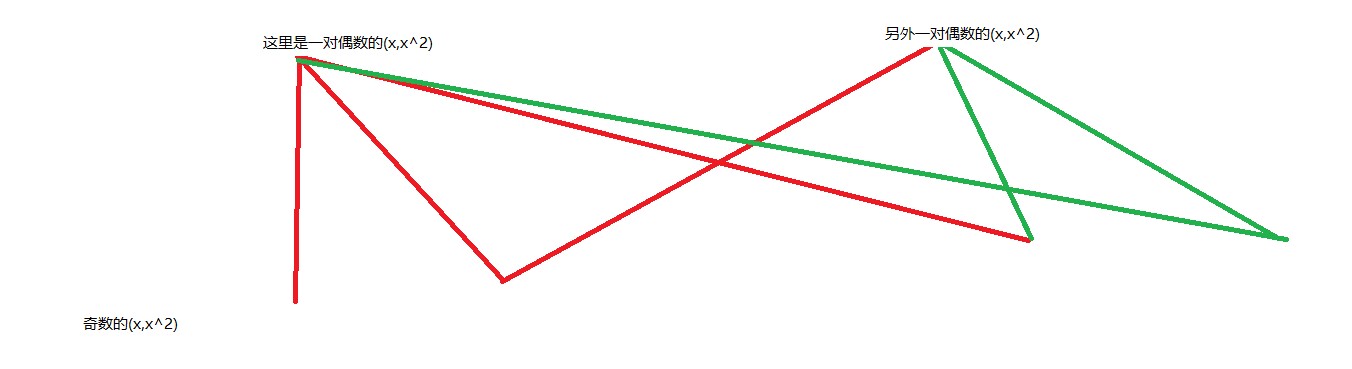
这是红绿简化情况（好二分的二分图哦）

然后来看我们压缩过的点，因为二分图要保证一边两点这样的结构不同色，所以我们这个图根据大图也是需要保证红/绿边与两个被压缩的点不同色

然后就不多说了就保证红边情况嘛，红边情况，不就是大家都有边吗，搞成4个不同颜色即可

然后问题就是说怎么去上色，来保证x,x^2和y,y^2不同色

1234这4种颜色，要根据编号分配到红色情况4个点，我们可以发现这四个点的编号%4他都不一样

奇数的两个是且一定是1或3，偶数两个是且一定是0或2，因为+2成对变换，所以就根据余数来分配咯

解决了红色情况，绿色也迎刃而解了，这个题就这样了

---

问题就是吧，n<=5，他没有红色情况

又是1又是2又是3的，非常不方便

打表算了，反正有6了就肯定有红色了，有红色就一定是4了，就取余数做了

嘻嘻

---

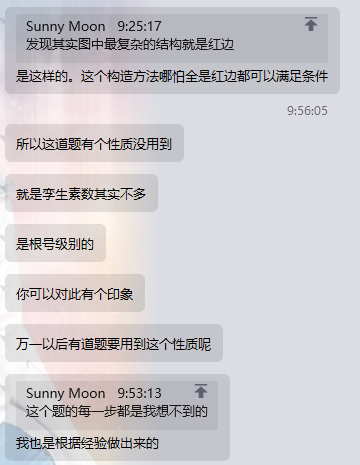
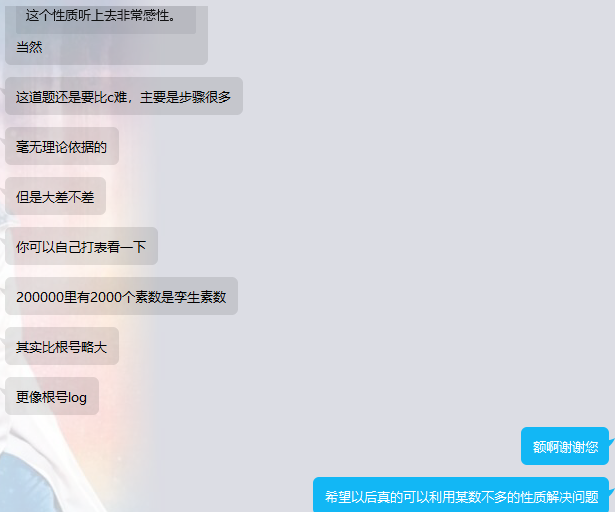
某数不多的性质

感性解题独门绝技

太可做了

这么些人都没做出来

终于心情舒畅了一天

---

诸君请看tj：

？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？

---