单调队列优化DP&斜率优化&四边形不等式

在本文中，我们将通过一道题来浅谈DP优化三大妈。

P3195 [HNOI2008] 玩具装箱 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

对于这种类型的题目，我们一般可以转化为如下形式：

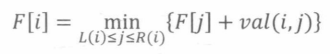
那么，$val(i,j)$ 又通常分为两种情况：

1. 其值仅与$i,j$中的一个有关。
2. 其值与$i,j$两者都有关。

单调队列优化DP

对于前者，我们有一个这样的例子：CF372C Watching Fireworks is Fun

那么我们一开始设的状态是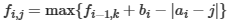：，可以化简为。

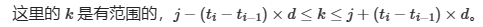
我们看到，由于$|a_i-j|+b_i$是常量，所以我们主要关心前者，也就是$k$。那么这里的$k$就相当于上面所述的j，他是与$i$无关的。

观察发现，最终$max$的取值只与上一状态中连续的一段的最大值有关，而这就相当于一个RMQ问题。不同的是，他是一个滑窗，于是我们就想到了单调队列来解决这个问题。将原来的$f_{i-1}$构造成一个单调队列，均摊复杂度为$O(1)$。

总结一下单调队列优化动态规划问题的基本形态：当前状态的所有值可以从上一个状态的某个连续的段的值得到，要对这个连续的段进行RMQ操作，相邻状态的段的左右区间满足非降的关系。关于详细操作，后面还会有所涉及。

而这类DP问题，我们统称为$1D/1D$的动态规划。（1D：单向组合）

斜率优化

对于后者，由于最终的决策与$i,j$均有关，不存在只与一方有关，我们需要将这个问题更抽象一步。

根据前人的经验，这类问题最终可以转化为这样的模型：

有一次函数$y=kx+b$，变量$y,k,x,b$之间相互有一些联系。现需要求得一种可行的方案，使得该函数与$y$轴交点纵坐标（截距）最小（或最大）。

我们直接以玩具装箱这道题来讲。最朴素的思想是：

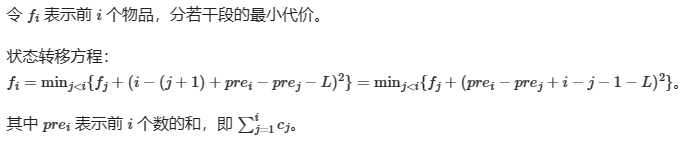
对其进行朴素的优化：

此时迎来了我们的重头戏。这个模型，是否与$b=y-kx$有几分相似呢？左边的$f_i-(s_i-L')^2$和$b$一样，都是我们想要最小化的内容。

我们像这样去做：

看到这里，您一定是一头雾水。您一定会想，$x-j,y_j,k_i,b_i$这些都是什么jb玩意儿？其实，这些一开始都是需要感性理解的。仔细观察发现，其实每一个这样的变量里面要么是常量，要么是只与$i,j$的其中一个有关的一些函数，说白了，就是一坨和类似于$i,j$这种东西变量。但这个变量不会是某种意义上的常量，您可以把$x,y,k,b$理解为函数。相当于是函数套函数，因此，当我们选择合法的$i,j$组合并在图上描点时，可以得到一下图像：

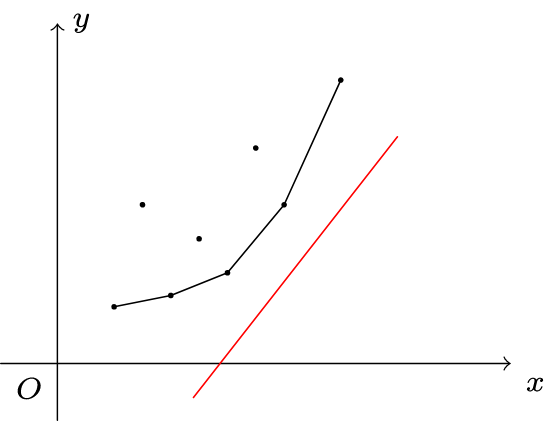
是许多零散的点。我们将位于凸包上的点用线连起来，大概就是这样。这时我们注意，$k_i$是一个定值。也就是说，最后我们选取的点得到的函数图像，其斜率一定为$k_i$。为什么要关注凸包呢？其实，求解这个问题，相当于将一条斜率为$k_i$的直线从下往上平移，落在这条直线上的第一个点就是答案了。因此不难得出，答案一定位于凸包上。

四边形不等式

如何能够证明单调队列维护的正确性呢？

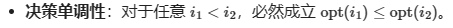
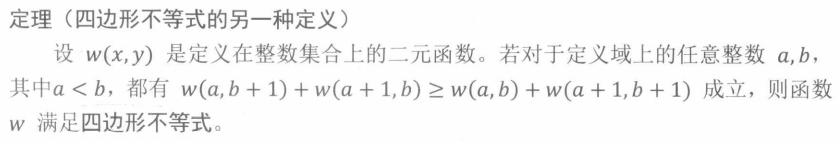
总体来说：

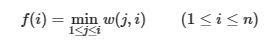如果可以证明w满足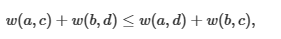

那么$f$就满足决策单调性。单调性那就可以各种优化，比如单调队列，二分等。

紧接着，我们证明在问题玩具装箱中的决策单调性：

最终，请看代码： 

#include<bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define rep2(i,a,b) for(int i=a;i<b;i++)
using namespace std;
const int INF=0x7fffffff;

const int N=5e4+5;
int n,L,head=1,tot,q[N],sum[N],dp[N];
int X(int j){return sum[j];}
int Y(int j){return dp[j]+(sum[j]+L)*(sum[j]+L);}
long double slope(int i,int j){
	return (long double)((Y(j)-Y(i))/(X(j)-X(i)));
}

signed main(){
	std::ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>L;
	L++;
	rep(i,1,n){
		cin>>sum[i];
		sum[i]+=sum[i-1]+1;
	}
	q[++tot]=0;
	rep(i,1,n){
		while(head<tot&&slope(q[head],q[head+1])<=2*sum[i])head++;
		dp[i]=dp[q[head]]+(sum[i]-sum[q[head]]-L)*(sum[i]-sum[q[head]]-L);
		while(head<tot&&slope(q[tot-1],q[tot])>=slope(q[tot-1],i))tot--;
		q[++tot]=i;
	}
	cout<<dp[n]<<endl;
	return 0;
}

To be continue...