模拟退火
超细讲解,超多例题,学习模拟退火必备文章。
算法简介
百度百科对模拟退火的介绍:link
你可能会一头雾水地进去,然后出来。但是不用怕,这一文,帮你搞定它!
- 此文专门研究信息学中模拟退火算法的应用。
对于模拟退火,它是由固体退火原理推出的,所以它很直观地被用来求解最小值。
将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温度升高变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
模拟退火建立在可靠的概率上,使得随机的正确率大大提升。“爬山算法”是另一种随机化求函数极值的算法,它只能求解局部最优解。
算法分析
- 先探究一元函数 \(y=f(x)\) 上的最小值问题。
在模拟退火过程中,我们定义 \(f(x_{ans})\) 为当前最小值,它有概率等于 \(\min f(x)\)。
定义 \(f(x)\) 为当前值,\(x\) 可能等于 \(x_{ans}\)。
从自变量推出因变量很简单,反之较难,所以我们记录 \(x\)。
而每一次退火,我们随机出一个 \(x'\),它可以和温度无关,也可以有关,但它必须和 \(x\) 有关。一般来说,我们在 \(x\) 附近的一定范围随机寻找一个 \(x'\)。
对于 \(f(x')\),若它比 \(f(x_{ans})\) 小,则符合我们寻找的对象,用 \(x'\) 更新 \(x_{ans}\) 和 \(x\)。
若 \(f(x')\ge f(x_{ans})\),显然它不满足我们当前的期望(虽然它有可能比当前解优,但不比当前最优解优),为了不让结果停留在局部最优解,我们考虑以一定的概率接受它。
\(x\) 就像 \(x_{ans}\) 派出的侦察兵,侦察比 \(x_{ans}\) 更小的值,而且替它接受 \(x'\)。
也就是说,接受它不同于 \(f(x')<f(x_{ans})\) 的情况,并不会改动 \(x_{ans}\),而只是改变 \(x\)。
定义 \(\Delta f=|f(x_{ans})-f(x')|\),显然 \(\Delta f\ge 0\)。
定义 \(T\) 为当前温度,它由初始温度乘上若干个温度变化量 \(\Delta T\) 得来,一般来说,初始温度为一个正整数,\(\Delta T\) 为一个 \((0,1)\) 的小数,模拟徐徐降温的过程。
则此概率为 \(e^{-\frac{\Delta f}{T}}\)。
由于 \(e^{-\frac{\Delta f}{T}}\) 为定值,\(T,\Delta f,e\) 都是固定的而不具有随机性,所以我们生成一个 \([0,1]\) 的随机数与它比较,使选择满足概率的随机性。
\(\Delta f\ge 0,T>0\to -\frac{\Delta f}{T}\leq 0\)
我们考虑 \(y=e^x\) 的图像:
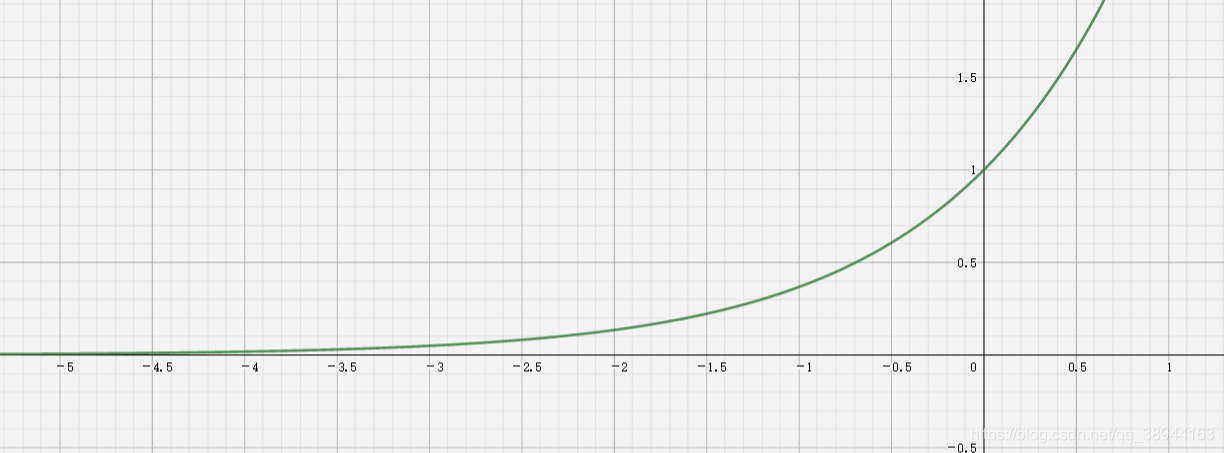
可以发现,\(e^{-\frac{\Delta f}{T}}\in(0,1]\),符合算法的描述。
直到 \(T\) 降到一个极小值 \(eps\) 以内,我们停止。
算法我们看懂了,可是若是想更进一步,比其他随机化算法更准,或者说是比其他人的模拟退火更准,需要我们明确的是 \(T,eps,\Delta T\) 的值。
- 更进一步的分析
假如当前最小值 \(f(x_{ans})\) 处于一个接近函数最小值的位置,显然,我们不希望它的侦察兵 \(x\) 再费时间去查看更大区域的值了,所以,越到后面,越难接受其他不优于当前解的值。
而实现这个突变,我们需要适当地对 \(T,eps\) 赋值。这个处于接近函数最小值就相当于快要结束退火,\(T\) 接近 \(eps\) 了。我们希望 \(e^{-\frac{\Delta f}{T}}\) 突然变得很小,不妨考虑 \(1\) 这个分界线。
乘法运算总是凌驾于加法运算之上,是因为它减轻了数量级对答案的影响。对于一个分母来说,乘上一个数之后使 \(\frac{\Delta f}{T}\) 变得很大(此时整个指数为负数),莫过于分母在 \(1\) 以下,越接近 \(0\) 越有效果。所以我们将 \(eps\) 设置为一个极小的小数,通常是 \(10^{-10}\) 以下。
\(T\) 不必设置很大,\(\Delta T\) 也不必设置很小。\(T\) 过大会导致初始时无法顾及全局,\(\Delta T\) 过小会导致变化过快,值不准确。
- 扩展到求解最大值
我们现在有专业人士分析的概率支撑最小值的求解,更不用说模拟退火在现实中也是内能减为最小。
而最大值需要一些推导。
我们现在想要求 \(f(x)\) 的最大值,不妨设 \(g(x)=-f(x)\),问题变成了求 \(g(x)\) 的最小值,我们来分析一遍。
生成 \(x'\)。
若 \(g(x')<g(x_{ans})\),即 \(f(x')>f(x_{ans}),x_{ans}=x=x';\)
反之 \(g(x')\ge g(x_{ans})\),即 \(f(x')\leq f(x_{ans})\),我们以 \(e^{-\frac{\Delta g}{T}}\) 的概率接受。
所以无论最大值还是最小值,由 Metropolis 准则推出的此概率都适用,只不过真正取值的时候如果不写绝对值函数,需要稍稍判断一下。并且 \(f\) 值的判段判断也要随之更改。
- OI 中的模拟退火
对于一道 OI 题,我们尝试用模拟退火解决它时,应先明确题目中状态。
将题目中的状态看成自变量,通过一个 \(x\) 到 \(y\) 的连线 \(f(x)\) 计算出该状态的值,然后进行模拟退火算法。
经典图:
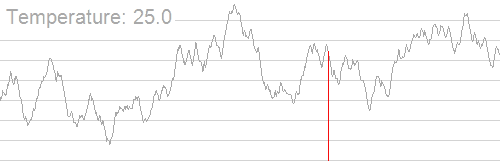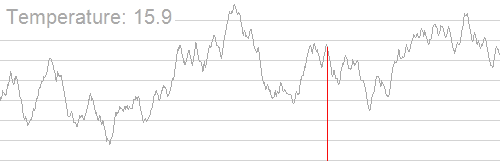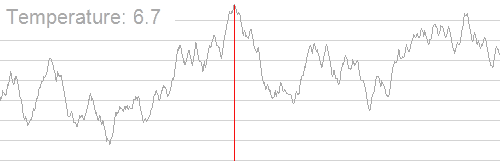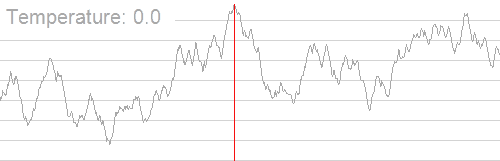
更多有关模拟退火算法的实战技巧我们结合例题分析。
例1:P1337 [JSOI2004]平衡点 / 吊打XXX
分析题目:求受力平衡点。
在受力不平衡时,物体会消耗能量运动到平衡点。在受力平衡时,物体的总能量最小。
所以根据 \(E_P=mgh=Gh\) 为重力势能,而重力 \(G\) 相当于是此题的 \(w_i\) 通过绳索传递到平面上,\(h\) 就转化成了绳结和小洞的距离。
即求:
的最小值,其中 \((x,y)\) 为绳结坐标。
初始解可以设为二维平面上的几何重心 \((\frac{1}{n}\sum x_i,\frac{1}{n}\sum y_i)\),可能会更接近答案(规则图形才有几何中心,而任何图形都有几何重心)。
几何重心是在不考虑重物的质量情况下(质量相等)确定的答案。
我们考虑如果此时受力不平衡,那绳结必定会向一个方向移动,我们将 \((x,y)\) 都随机移动一些,根据模拟退火求解即可。
因为初始点与答案相差不会太大并且 \(f(x,y)=\sum_{i=1}^nw_i\times\sqrt{(x-x_i)(y-y_i)}\) 是一个二元的“单峰函数”(二维似乎不能称单峰,但是我们可以固定 \(x\) 或 \(y\),变成一元),所以我们的偏移量 \(\Delta x,\Delta y\) 不用太大,也就是 \(T\) 也不用太大。但是对于 eps 任何时候都小一点为好。
代码:
const int N=2e3+5;
const double eps=1e-6,MAX_TIME=0.9;
struct node{
int x,y,w;
}a[N];
double ansx=0,ansy=0,answ=0;
int n,m;
double calc(double x,double y){
double dis=0,dx,dy;
for(int i=1;i<=n;++i){
dx=x-a[i].x;
dy=y-a[i].y;
dis+=sqrt(dx*dx+dy*dy)*a[i].w;
}
return dis;
}
void sa(){
double T=3033;
while(T>eps){
double nx=T*(rand()*2-RAND_MAX)+ansx;
double ny=T*(rand()*2-RAND_MAX)+ansy;
double nw=calc(nx,ny);
double delta=nw-answ;
if(delta<0)ansx=nx,ansy=ny,answ=nw;
else if(exp(-delta/T)*RAND_MAX>rand())ansx=nx,ansy=ny;
T*=0.998;
}
}
int main(){
srand(time(0));
n=read();
for(int i=1;i<=n;++i){
a[i].x=read(),a[i].y=read(),a[i].w=read();
ansx+=a[i].x,ansy+=a[i].y;
}
ansx/=n,ansy/=n;
answ=calc(ansx,ansy);
while((double)clock()/CLOCKS_PER_SEC<MAX_TIME)sa();
cout<<fixed<<setprecision(3)<<ansx<<" "<<setprecision(3)<<ansy;
return 0;
}
注意事项:
-
程序开始时设置的
srand(time(0))为将当前系统时间作为种子,建议不要用固定数值的种子。 -
\(T\) 的初值设置要根据题目数值范围而定,因为此题中 \(T\) 的大小影响着偏移量
rand()*2-RAND_MAX。 -
定义
eps为极小量来终止模拟退火,对于保留 \(x\) 位小数的题目,建议eps的大小不要超过1e-2x,可以更小(要不然你可能连样例也过不了)。 -
模拟退火可以用来求最大值或最小值,其区别就是在对答案的更新上。记 \(nw\) 为当前解,\(answ\) 为之前最优解。若求的是最小值,则当 \(nw<answ\) 时访问它;当 \(nw\ge answ\) 时,我们随机一个 \([0,1]\) 之间的概率,将其与 \(e^\frac{-\Delta f}{T}\) 进行比较,小于 \(e^\frac{-\Delta f}{T}\) 则访问。
-
再次重申!访问只是不改变决策或是更新位置、状态,而不是更新答案!!!
-
对于 \(e^\frac{-\Delta f}{T}\),指数 \(-\frac{\Delta f}{T}\) 是一个负数,随 \(T\) 的降低而减小,也就对应了越到后面越精确的退火过程。
-
对于判断是否访问非最优解时与 \(e^\frac{-\Delta f}{T}\) 比较的随机概率,建议不要用
rand()/RAND_MAX,因为这是两个整数相除,变成浮点数也会影响精度,所以可以将RAND_MAX乘到左边。 -
rand()*2-RAND_MAX可以使随机数从正数到负数,符合此题在二维平面上任意方向移动的情况。 -
对于 \(\Delta T\),建议在 \(0.9\) 以上,并且保证稳定的过样例。
-
rand()在 Windows 系统下生成 \([0,2^{15}-1]\) 的数,而在 Linux 系统下生成 \([0,2^{31}-1]\) -
在家做题:此题的偏移量不是很大,因为 \(|x|,|y|\leq 10^4\),所以只需要用
rand()即可。对于超过 \(2^{15}\) 的随机数生成,可以用(rand()<<15|rand())。对于 \(mt19937\),虽然生成的随机数质量很高,但是偏大,并且最大值能达到 \(2^{32}-1\) 超过int,若用int会返回负值。 -
考场做题:NOIP 考场使用 Linux 系统,所以不用管!!!
-
对于一次退火指的是温度从初始值降到
eps以下,然鹅有时候一次退火可能不够,所以我们在时限内尽可能地跑 SA:while((double)clock()/CLOCKS_PER_SEC<MAX_TIME)sa(); -
可以的话,配合暴力对拍调参,当然此题不太好写暴力。
-
一次模拟退火的时间复杂度一般来说是 \(O(n\log_{\Delta T}\frac{eps}{T})\),依照此题计算数值大约是 \(2000\times\log_{0.998}\frac{10^{-15}}{3033}\approx2000\times21257\approx42514000\) ,其中 \(n\) 是计算当前解花费的时间。
例2:P3878 [TJOI2010]分金币
我们将其分成两个集合,大小分别为 \(\frac{n}{2},n-\frac{n}{2}\),每次随机交换两个集合中的两个元素,然后进行判断即可。
从此题中我们又能学到一些东西:
-
多组数据不建议用卡时间
while的方法,因为不好判断每一组。建议在计算时间后对每一组跑固定次数,比如说 \(100\) 次。for(int i=1;i<=100;++i)sa(); -
那么为什么跑一百次的时候不用一个变量来记录这一百次的最小值(最优解)呢?根本不用记录,因为
ans代表的就是最优解,每次只有在遇见更优的时候才会改变它的值,其他时候只是改变位置、状态。 -
如果你的模拟退火跑到了比数据答案还优的解,大概率是你写错了。
-
这题可以 \(O(n)\) 求出当前解,但也可以 \(O(1)\)。
-
模拟退火有个和二分很像的特点,他们都是枚举新的位置、状态,然后花一些时间去计算当前解,然后判断当前解优不优。接着模拟退火可以概率性跳出,而二分则不会跳出。一个求多峰函数,一个求单峰函数。
-
最好和暴力对拍,此题就可以写暴力,多拍一会。
-
为什么这一题可以随机选两个集合中的两个数呢?一是根据提议不同,符合题意最优更好;二是偏移量本就和 \(T\) 没关系,侧面体现出 \(e^{-\frac{\Delta f}{T}}\) 中在最后时 \(T\) 的重要性:最大概率地排除错解。
-
当在最后关头,若在最优解旁边徘徊,就不能再花费时间去跳出峰值区域找其他的,所以最后的概率不仅要变小,而且变化率也要变大。所以一般我们会将 \(T\) 初值定义在几千,而末值定义为一个极小的数,这是因为极小的数对概率减小的变化量大。使得:越到后面,跳出概率越小,而且变小的速度越快。
-
温度 \(T\),温度变化量 \(\Delta T\),以及
RAND_MAX,rand(),前两者必须用double类型!!!!!
const int N=35;
const double eps=1e-15;
int t,n,a[N],ans,sum1,sum2;
int calc(){
int sum1=0,sum2=0;
for(int i=1;i<=n;++i){
if(i<=n/2)sum1+=a[i];
else sum2+=a[i];
}
return sum1>sum2?sum1-sum2:sum2-sum1;
}
void sa(){
double T=5000;
while(T>eps){
int x=rand()%(n/2)+1,y=rand()%(n-n/2)+n/2+1;
swap(a[x],a[y]);
int nans=calc();
if(nans<ans)ans=nans;
else if(exp((ans-nans)/T)*(double)RAND_MAX<(double)rand())swap(a[x],a[y]);
T*=0.999;
}
}
signed main(){
srand(time(0));
t=read();
while(t--){
n=read();
for(int i=1;i<=n;++i)a[i]=read();
if(n==1){print(a[1]),puts("");continue;}
ans=calc();
for(int i=1;i<=100;++i)sa();
print(ans),puts("");
}
return 0;
}
例3:P2503 [HAOI2006]均分数据
将 \(n\) 个整数 \(a_i\) 分成 \(m\) 组,使 \(\sigma = \sqrt{\frac 1m \sum\limits_{i=1}^m(\overline x - x_i)^2}\) 最小,其中 \(x_i\) 为第 \(i\) 组的数据和,\(\overline x = \frac 1m \sum\limits_{i=1}^m x_i\)。
\(n\leq 20,m\leq 6,a_i\in[1,50]\)
此题的分成 \(m\) 组显然不是将 \(n\) 个数分成连续的 \(m\) 段,若为后者,\(dp\) 即可。
考虑转化,首先有一个绝对正确的暴力,枚举全排列,\(dp\) 计算,复杂度 \(O(n!\times n^2m)\)。可以用来对拍。
考虑模拟退火,随机选两个数交换,然后进行 \(dp\),适当调整温度。
- 注意 \(dp\) 的初始化,我一开始没将 \(f[0][1],f[1][0]\) 赋值为无穷大,WA 了 \(6\) 发。
const int N=25,M=10;
const double MAX_TIME=0.9,eps=1e-8;
int n,m;
double a[N],f[N][M],sum[N],X,ans;
double calc(){
for(int i=0;i<=n;++i){for(int j=0;j<=m;++j)f[i][j]=1e9;sum[i]=0;}
f[0][0]=0;
for(int i=1;i<=n;++i)sum[i]=sum[i-1]+a[i];
for(int i=1;i<=n;++i){
for(int k=0;k<=i-1;++k){
for(int j=1;j<=m;++j){
if(j>i||j-1>k)break;
f[i][j]=min(f[i][j],f[k][j-1]+(X-sum[i]+sum[k])*(X-sum[i]+sum[k]));
}
}
}
return sqrt(f[n][m]/m);
}
void sa(){
double T=5008;
while(T>eps){
int x=rand()%n+1,y=rand()%n+1;
swap(a[x],a[y]);
double nans=calc();
if(nans<ans)ans=nans;
else if(exp((ans-nans)/T)*(double)RAND_MAX<(double)rand())swap(a[x],a[y]);
T*=0.998;
}
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;++i)a[i]=read(),X+=a[i];
X/=m;
ans=calc();
while((double)clock()/CLOCKS_PER_SEC<MAX_TIME)sa();
cout<<fixed<<setprecision(2)<<ans;
return 0;
}
到此,你已经差不多理解了模拟退火的意义和写法,来写一道题练习一下吧!
P2210 Haywire
- 从以上题目可以发现,模拟退火适用于一些 \(n\) 不是很大的情况,也可以用于一道题部分数据的骗分。
- 若可以写阶乘或状压暴力,可以考虑写暴力对拍。
例4:P1248 加工生产调度
这题是一个很难理解的贪心,所以我们直接模拟退火。
首先若给出一个 \(1\sim n\) 的排列,我们可以在 \(O(n)\) 的时间复杂度内计算出按这个排列进行加工所得到的答案。
初始答案定义为 \(1\sim n\) 的递增排列以及它计算出的答案。
注意:此题最后的答案是最少加工时间以及对应的加工顺序,所以我们还要开一个数组来记录顺序。并且这个数组和 \(ans\) 一样,只在答案更优是改变,而不在概率判断时改变!!!
对于偏移量,我们随机交换排列中的两个数。
显然有一个 \(O(n!\times n)\) 的暴力,我们那来对拍。
- 明确一道题里面你代码中维护的变量作用、是否能够变化。
const int N=1e3+5;
const double eps=1e-16,MAX_TIME=0.97;
int n,a[N],b[N],ans,p[N],pans[N];
int calc(){
int A=0,B=0;
for(int i=1;i<=n;++i){
A+=a[p[i]];
if(A>B)B=A+b[p[i]];
else B+=b[p[i]];
}
return max(A,B);
}
void sa(){
double T=5000;
while(T>eps){
int x=rand()%n+1,y=rand()%n+1;
swap(p[x],p[y]);
int nans=calc();
if(nans<ans){ans=nans;for(int i=1;i<=n;++i)pans[i]=p[i];}
else if(exp((double)(ans-nans)/T)*(double)RAND_MAX<rand())swap(p[x],p[y]);
T*=0.998;
}
}
signed main(){
n=read();
for(int i=1;i<=n;++i)a[i]=read(),p[i]=pans[i]=i;
for(int i=1;i<=n;++i)b[i]=read();
ans=calc();
while((double)clock()/CLOCKS_PER_SEC<MAX_TIME)sa();
print(ans),puts("");
for(int i=1;i<=n;++i)print(pans[i]),printf(" ");
return 0;
}
例5:P5544 [JSOI2016]炸弹攻击1
首先我们看一下 \(y=e^x\) 的图像:

可以发现,exp(x) 函数,也就是 \(y=e^x\) 在 \(x\leq0\) 时范围在 \((0,1]\),此时符合模拟退火的要求。另一侧为 \(rand()/RAND\_MAX\in [0,1]\)。
所以无论在求最大值还是最小值,我们在使用模拟退火算法时都要保证 exp 里的数小于等于 \(0\)。
- 模拟退火算法是基于此概率的,一定不要搞错。
然鹅,如果我说模拟退火过不掉这题——确实过不掉。
在这题的题解里,许多人用的都是错误的代码,没有按照本文算法分析的结果来写,导致几乎全部为爬山算法。
本人使用各种优化和乱搞加强模拟退火的正确性,也只不过是在 \(30\sim 40\) 分徘徊。
那么,为什么这题爬山算法能过,而模拟退火不行呢?
模拟退火不能过的原因很好解释,模型太过困难,函数过于奇葩。这题的函数是什么呢?吧函数变成状态对应值,它可能长这样:
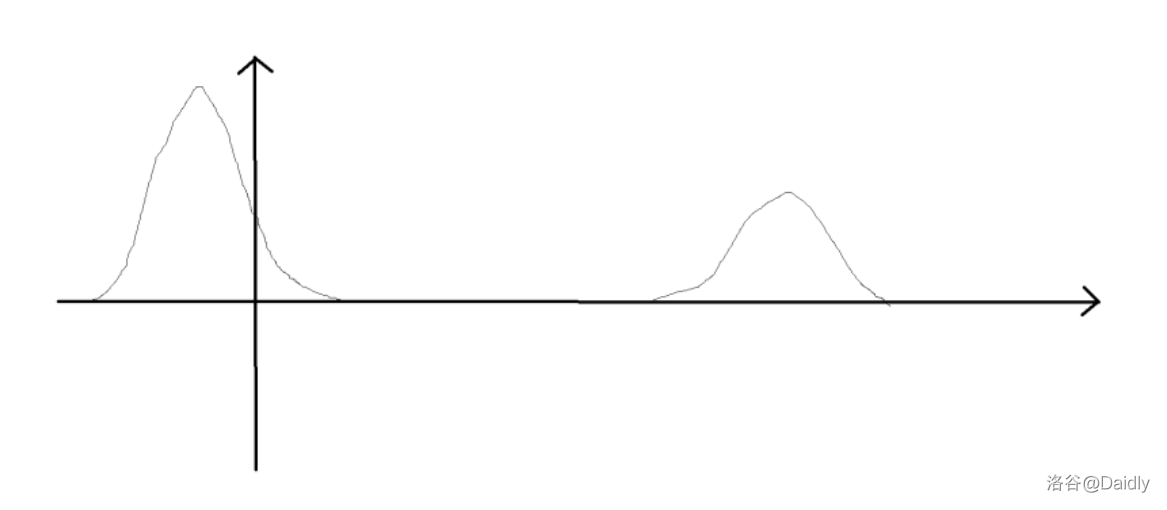
看起来就很丑(
而爬山算法能过的依据是什么呢?
所以这题并不适合作为模拟退火的练习题,并且爬山算法的正确性不能保证。这题的正解是正经算法,计算几何,有兴趣的同学可以看 link。
例6:P2538 [SCOI2008]城堡
最短路 trick+模拟退火
最短路的 trick 就是:在 \(n\) 个点中有 \(m\) 个特殊点,求剩下 \(n-m\) 个点到这些特殊点最短路最大值。
对于有向图,我们建出反图,再建立虚点链接 \(m\) 个特殊点,从虚点跑一次单源最短路,得到的最短路最大值即为答案;对于无向图,省去建反图的操作,其余相同。
随机交换两个集合中的两个点,计算即可。
const int N=55;
const double MAX_TIME=0.7,eps=1e-15;
int n,m,k,r[N],num,p[N],dis[N];
bool f[N],vis[N];
int ans;
struct edge{
int next,to,w;
}e[N<<1];
int head[N],cnt;
void add(int from,int to,int w){
e[++cnt].w=w;
e[cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
struct node{
int u,dis;
bool operator>(const node &p)const{return dis>p.dis;}
};
priority_queue<node,vector<node>,greater<node> >q;
void dij(){
for(int i=1;i<=n;++i)dis[i]=0,vis[i]=0;
for(int i=k+1;i<=num;++i)dis[p[i]]=1e9;
for(int i=1;i<=n;++i)if(f[i])q.push({i,0});
for(int i=1;i<=k;++i)q.push({p[i],0});
while(!q.empty()){
int u=q.top().u;
q.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to,w=e[i].w;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push({v,dis[v]});
}
}
}
}
int calc(){
dij();
int maxn=0;
for(int i=k+1;i<=num;++i)maxn=max(maxn,dis[p[i]]);
return maxn;
}
void sa(){
double T=2008;
while(T>eps){
int x=rand()%k+1,y=rand()%(num-k)+1+k;
swap(p[x],p[y]);
int nans=calc();
if(nans<ans)ans=nans;
else if(exp((double)(ans-nans)/T)*(double)RAND_MAX<(double)rand())swap(p[x],p[y]);
T*=0.998;
}
}
int main(){
n=read(),m=read(),k=read();
for(int i=1;i<=n;++i){
r[i]=read()+1;
}
for(int i=1;i<=n;++i){
int d=read();
add(i,r[i],d);
add(r[i],i,d);
}
for(int i=1;i<=m;++i)f[read()+1]=1;
for(int i=1;i<=n;++i)if(!f[i])p[++num]=i;
if(num<=k){puts("0");return 0;}
ans=calc();
while((double)clock()/CLOCKS_PER_SEC<MAX_TIME)sa();
print(ans);
return 0;
}
一道练习题:P3936 Coloring
我的评价是:一道超级恶心的模拟退火题。
如果你能独立完成这道题,说明你对模拟退火的掌握情况已经差不多了。
- \(O(1)\) 计算。除了初始值 \(O(nm)\) 计算之外,模拟退火中状态的值必须 \(O(1)\) 计算,否则以这题的困难情况,几乎腾不出时间跑模拟退火。
- 初温设小,\(\Delta T\) 设大。
- 能跑就多跑。
总结
模拟退火可以用来在考试中骗取客观的部分分,不妨将它与暴力融合。
没有什么好总结的了,前面注意事项都说过了。
完结撒花!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号