PTA1-3次作业总结与分析
一、前言
1.难度分析
前两次作业比第三次作业相对轻松,因此以下内容主要围绕第三次作业,此外也会稍稍提到第二次作业的第二小题。
2.题量分析
看起来前两次作业题量很多,其实第三次作业花费的时间比前两次的时间加起来还要多。
3.知识点
2-7-2 串口字符解析
奇偶校验:分为奇校验和偶校验两种,区分相反。
奇检验:有效数据中“1”的个数为偶数时,校验位应为“1”;个数为奇数时,校验位应为“0”。
偶检验:有效数据中“1”的个数为奇数时,校验位应为“1”;个数为偶数时,校验位应为“0”。
3-7-1 点线形系列1-计算两点之间的距离
设两个点坐标 A(x1,y1),B(x2,y2) ,则A和B两点之间的距离为:
∣AB∣=√[(x1-x2)²+(y1-y2)²]
3-7-2 点线形系列2-线的计算
1.直线公式Ax+By+C=0 ,斜率公式为:
k=-A/B
2.点(x0,y0)与直线的垂直距离:
|A*x0+B*y0 +C|/√A²+B²
3.判断三点一线,有两种判定方法(实际上是一种):
1)先求出两点的直线公式,代入第三点坐标,若值为0则在直线上,否则不在。
2)点与直线距离为0,可直接调用问题2算法。
4.判断直线是否平行:
斜率是否相等(不存在另起判断)
5.点a,b构成直线ab公式:A1x+B1y+C1=0;点c,d构成直线cd公式:A2x+B2y+C2=0
(1)求两直线交点intersection:
intersection.x = (C2 * B1 - C1 * B2) / (A1 * B2 - A2 * B1)
intersection.y = (C1 * A2 - C2 * A1) / (A1 * B2 - A2 * B1)
相交:(A2*a.x+B2*a.y+C2)*(A2*b.x+B2*b.y+C2)<=0
不相交:(A2*a.x+B2*a.y+C2)*(A2*b.x+B2*b.y+C2)>0
3-7-3 点线形系列3-三角形的计算
1.判断是否是等腰三角形、等边三角形:
等腰三角形:ab=bc||ab=ac||bc=ac(存在两边长度相等)
等边三角形:ab=bc&&ab=ac&&bc=ac(任意两边长度相等)
2.输出周长、面积、重心坐标:
周长 :
C=(ab+bc+ac)
海伦公式求面积 :
P=C/2,S=√(p*(p-ab)*(p-bc)*(p-ac))
重心坐标bar(bar.x,bar.y):
bar.x=(a.x+b.x+c.x)/3;
bar.y=(a.y+b.y+c.y)/3;
3.判断是钝角、直角还是锐角三角形:
直角:存在一角cos=0
钝角:存在一角cos>0
锐角:任意一角cos<0
4.前两个点所在的直线与三个点所构成的三角形相交:
1)交点数量:异侧参考
0个:三角形三点均在直线同侧
1个:直线过三角形其中一个端点,且三角形另外两个端点均在直线同侧
2个:上面情况除外/下面求面积详谈
2)分割面积,分两种情况:
直线过三角形其中一个端点且直线交三角形一边:求出其中一个三角形面积,再用总三角形面积相减得到另一部分面积。
直线交三角形两边(直线不过三角形一个端点):先找出哪两个点在同侧,那么三角形另外一点与两交点形成一个分割三角形,求出这个三角形面积,再用总三角形面积相减得到另一部分面积。
5.判断点a是否在三角形bcd内部:
通过点与三角形端点构成的三个三角形面积之和与原三角形面积相比:
三角形abc面积为S1
三角形acd面积为S2
三角形abd面积为S3
三角形bcd面积为S
点在三角形内:S=S1+S2+S3
点在三角形外:S>S1+S2+S3
二、设计与分析
第二次大作业
2-7-2 串口字符解析
源码:
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner input=new Scanner(System.in);
String S=input.nextLine();
char []s=S.toCharArray();
int i,j,jishu=0,n,cixu=1,status=0,flag;
for(i=0;i<s.length;i++){
if(s[i]=='0'){
jishu=s.length-i;
break;
}
}
if(jishu<11){
System.out.print("null data");
}else{
for(i=0;i<s.length;i++){
if(s[i]=='0'&&s.length-i>=11){
n=0;//记录8位有效数据中奇数个数【0,8】
status=0;//状态重置
flag=0;//输出序号标记
if(flag==0){
System.out.print(cixu+":");
flag=1;
cixu++;
}
for(j=i+1;j<i+9;j++){//判断8位有效数据中奇数个数
if(s[j]=='1')
n++;
}
if((n+1)%2==s[j]-48&&s[j+1]!='1')//判断奇校验位和结束位
status=1;//状态1
if((n+1)%2!=s[j]-48&&s[j+1]=='1')//判断奇校验位和结束位
status=2;//状态2
if((n+1)%2!=s[j]-48&&s[j+1]!='1')//判断奇校验位和结束位
status=3;//状态3
//System.out.print(status);
switch (status){
case 0:
for(j=i+1;j<i+9;j++)
System.out.print(s[j]);
System.out.println("");
break;
case 1:System.out.println("validate error");break;
case 2:System.out.println("parity check error");break;
case 3:System.out.println("validate error");break;
}
i+=10;
}
}
}
}
}
SourceMonitor的生成报表内容:
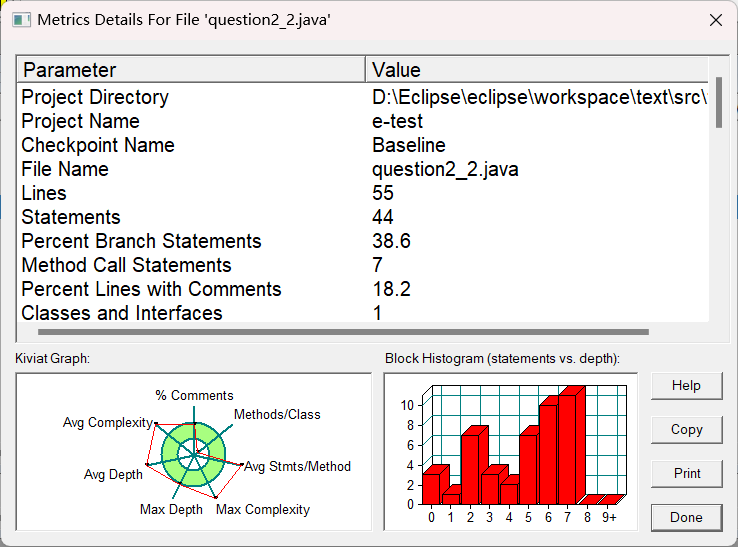
因嵌套了太多的if/else导致代码几乎大部分都不合格,平均复杂度是15,远远超过绿色范围(所推荐的java良好代码,如平均复杂度在2.0-4.0之间)
第三次大作业
在作代码分析前,先将我的三类方法:点,线,三角形放置如下,以避免过长的代码冗余,个人建议先将类方法和Main分别放进编辑器(Eclipse),按住Ctrl键后将鼠标移至Main的方法引用,可查询相应的方法。以下并非提交的PTA源码,因提交后优化了部分代码,但大体上是不变的。
如果不需要查看类代码,建议点击跳过
点类:
class point{
double x,y;
//----------------------------------------------------------
/* 输入:所有点的字符串 String
* 输出:输入是否合法 boolean
* 功能:判断输入是否合法
*/
public static boolean islegal(String s,int weidu) {
String []sp1=s.split(" ");
String []sp2;
for(String i:sp1){
sp2=i.split(",");
if(sp2.length!=weidu) {
return false;
}
for(String j:sp2){
if(!j.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
return false;
}
}
}
return true;
}
//----------------------------------------------------------
/* 输入:所有点的字符串 String
* 输出:点的个数 int
* 功能:返回点的个数
*/
public static int get_length(String s){
String []sp1=s.split(" ");
return sp1.length;
}
//----------------------------------------------------------
/* 输入:所有点的字符串 String
* 输出:一个点的坐标
* 功能:返回第i点的坐标
*/
public void get_point(String s,int i){
String []sp1=s.split(" ");
String []sp2=sp1[i-1].split(",");
this.x=Double.valueOf(sp2[0]);
this.y=Double.valueOf(sp2[1]);
}
//----------------------------------------------------------
/* 输入:另外一个点对象 point
* 输出:两点间距离 double
* 功能:计算两点间距离
*/
public double distance(point m){
return Math.sqrt((this.x-m.x)*(this.x-m.x)+(this.y-m.y)*(this.y-m.y));
}
//----------------------------------------------------------
/* 输入:另外一个点对象 point
* 输出:两点是否相同 boolean
* 功能:判断两点是否相同
*/
public boolean is_coi(point m){
if(this.x==m.x&&this.y==m.y)
return true;
return false;
}
}
线类:
class line {
double A,B,C;//直线公式:Ax+By+C=0
//----------------------------------------------------------
/* 输入:两点 point
* 输出:无
* 功能:通过两点坐标获取直线方程
*/
public void get_line(point b,point c) {
this.A=c.y-b.y;
this.B=b.x-c.x;
this.C=c.x*b.y-b.x*c.y;
}
//----------------------------------------------------------
/* 输入:另外一个点对象 point
* 输出:两点形成直线的斜率是否存在 boolean
* 功能:判断两点两点形成直线的斜率是否存在,前提两点不重合
*/
public boolean slope_exist(){
if(this.B==0)
return false;
return true;
}
//----------------------------------------------------------
/* 输入:两点 point
* 输出:斜率 double
* 功能:计算两点直线斜率
*/
public double slope_calculation() {
return (-1*A/B);
}
//----------------------------------------------------------
/* 输入:三点 point
* 输出:点到直线距离 double
* 功能:计算第一个点与另外两点连线的垂直距离
*/
public static double ptol_dis(point a,line bc) {
return (Math.abs(bc.A*a.x+bc.B*a.y+bc.C)/Math.sqrt(bc.A*bc.A+bc.B*bc.B));
}
//----------------------------------------------------------
/* 输入:一点一线 point,line
* 输出: boolean
* 功能:判断点a是否在直线bc上
*/
public static boolean is_point_on_edge(point a,line bc) {
if(Math.abs(line.get_ponl(a,bc))<1e-6)//范围精度
return true;
return false;
}
//----------------------------------------------------------
/* 输入:两条直线 line
* 输出:交点 point
* 功能:计算两条直线的交点
*/
public static point get_intersection(line ab,line cd) {
point intersection = new point();
intersection.x = (cd.C * ab.B - ab.C * cd.B) / (ab.A * cd.B - cd.A * ab.B);
intersection.y = (ab.C * cd.A - cd.C * ab.A) / (ab.A * cd.B - cd.A * ab.B);
return intersection;
}
//----------------------------------------------------------
/* 输入:一条线段,两个点 line,point
* 输出: boolean
* 功能:判断相交点是否在两条线段内
*/
public static boolean is_interset(line ab,point c,point d) {
if((ab.A*c.x+ab.B*c.y+ab.C)*(ab.A*d.x+ab.B*d.y+ab.C)<=1e-12){
/* 原理:将其中一条线段的两个端点分别代入另一条线段的公式中,表示在端点上作两条平行于另一条线段的直线,
* 得到的值等于0表示在点在直线上,若相交点在两条线段内,得到的两个值必然一正一负或者存在一个0值,可以通过画图证明
*/
return true;
}
return false;
}
//----------------------------------------------------------
/* 输入:两条线段 line
* 输出: boolean
* 功能:判断两条线是否平行
*/
public static boolean is_parallel(line ab,line cd) {
if((ab.slope_calculation()==cd.slope_calculation())||(!ab.slope_exist()&&!cd.slope_exist())){
return true;
}
return false;
}
//----------------------------------------------------------
/* 输入:线段,点 line,point
* 输出:方程值 double
* 功能:判断一个点是否在直线上
*/
public static double get_ponl(point c,line ab) {
return ab.A*c.x+ab.B*c.y+ab.C;
}
}
三角形类:
import java.util.Arrays;
class triangle {
point a = new point();
point b = new point();
point c = new point();
line ab = new line ();
line ac = new line ();
line bc = new line ();
/*
* 输入:原始点的字符串 String
* 输出:点的个数是否合法 boolean
* 功能:判断点的个数是否合法
*/
public boolean legal_pnum(String s) {
if(point.get_length(s)!=3)
return false;
return true;
}
/*
* 输入:原始点的字符串 String
* 输出: boolean
* 功能:判断能否构成三角形
*/
public boolean legal_form() {
if(this.a.is_coi(this.b)||this.a.is_coi(this.c)||this.b.is_coi(this.c)||line.is_parallel(this.ab,this.bc))
return false;
return true;
}
/*
* 输入:原始点的字符串,字符串的三个点索引值,如第一个点索引值为1 String,int
* 输出:
* 功能:根据字符串获取三角形的三点和三边
*/
public void get_triangle(String s,int i,int j,int k) {
this.a.get_point(s,i);
this.b.get_point(s,j);
this.c.get_point(s,k);
this.ab.get_line(this.a,this.b);
this.bc.get_line(this.c,this.b);
this.ac.get_line(this.a,this.c);
}
/*
* 输入:两个点 point
* 输出:长度 double
* 功能:获取边的长度
*/
public double get_line_length(point a,point b) {
return a.distance(b);
}
/*
* 输入:无
* 输出:无
* 功能:判断是否为等腰三角形
*/
public boolean is_iso() {
double AB=this.a.distance(this.b);
double BC=this.c.distance(this.b);
double AC=this.a.distance(this.c);
if(AB==AC||AB==BC||BC==AC)
return true;
return false;
}
/*
* 输入:无
* 输出:无
* 功能:判断是否为等边三角形
*/
public boolean is_equ() {
double AB=this.a.distance(this.b);
double BC=this.c.distance(this.b);
double AC=this.a.distance(this.c);
if(AB==AC&&AB==BC&&BC==AC)
return true;
return false;
}
//----------------------------------------------------------
/* 输入:无
* 输出:周长 double
* 功能:输出三角形的周长
*/
public double get_perimeter() {
double AB=this.a.distance(this.b);
double BC=this.c.distance(this.b);
double AC=this.a.distance(this.c);
return AB+BC+AC;
}
//----------------------------------------------------------
/* 输入:无
* 输出:周长 double
* 功能:输出三角形的面积(海伦公式)
*/
public double get_area() {
double AB=this.a.distance(this.b);
double BC=this.c.distance(this.b);
double AC=this.a.distance(this.c);
double p=(AB+BC+AC)/2;
return Math.sqrt(p*(p-AB)*(p-BC)*(p-AC));
}
//----------------------------------------------------------
/* 输入:无
* 输出:重心点 point
* 功能:输出三角形的重心
*/
public point get_gra() {
point bar=new point();
bar.x=(this.a.x+this.b.x+this.c.x)/3;
bar.y=(this.a.y+this.b.y+this.c.y)/3;
return bar;
}
//----------------------------------------------------------
/* 输入:原始数据 ,保留小数点后位数 double,int
* 输出:四舍五入后的数 double
* 功能:保留小数点后n位,多余部分采用四舍五入规则进到最低位
*/
public static double round(double m,int n) {
return (double)Math.round(m*Math.pow(10,n))/Math.pow(10,n);
}
//----------------------------------------------------------
/* 输入:无
* 输出:三个角的cos值数组 double[]
* 功能:获取三角形的三个角的cos值,排列顺序按输入点时的顺序
*/
public double[] get_cos() {
double []cos=new double[3];
double AB=this.a.distance(this.b);
double BC=this.c.distance(this.b);
double AC=this.a.distance(this.c);
cos[0]=(AC*AC+AB*AB-BC*BC)/(2*AC*AB);
cos[1]=(BC*BC+AB*AB-AC*AC)/(2*BC*AB);
cos[2]=(BC*BC+AC*AC-AB*AB)/(2*BC*AC);
return cos;
}
//----------------------------------------------------------
/* 输入:无
* 输出:'=','>','<' 三种char char
* 功能:判断三角形是直角,钝角还是锐角三角形,返回'='为直角三角形,'>'为钝角三角形,'<'为锐角三角形
*/
public char compare_90angle() {
double cosA=this.get_cos()[0];
double cosB=this.get_cos()[1];
double cosC=this.get_cos()[2];
if(Math.abs(cosA)<1e-6||Math.abs(cosB)<1e-6||Math.abs(cosC)<1e-6){//小数点后六位精度范围内判定为直角三角形
return '=';
}else if(cosA*cosB*cosC<0){//存在唯一一个角度大于90度,其cos值小于0
return '>';
}else{
return '<';
}
}
//----------------------------------------------------------
/* 输入:直线上的两个点,三角形 point,triangle
* 输出: boolean
* 功能:判断直线ab是否在三角形cde边上
*/
public boolean is_line_on_edge (point a,point b) {
line cd=this.ab;//三角形其中一边
line ce=this.ac;
line de=this.bc;
if(((Math.abs(line.get_ponl(a,cd))<1e-6)&&(Math.abs(line.get_ponl(b,cd))<1e-6))
||(Math.abs(line.get_ponl(a,ce))<1e-6)&&(Math.abs(line.get_ponl(b,ce))<1e-6)
||(Math.abs(line.get_ponl(a,de))<1e-6)&&(Math.abs(line.get_ponl(b,de))<1e-6)){
return true;
}
return false;
}
//----------------------------------------------------------
/* 输入:点,三角形 point,triangle
* 输出: boolean
* 功能:判断点a是否在三角形bcd边上
*/
public boolean is_point_on_edge (point a) {
if((Math.abs(line.get_ponl(a,this.ab))<1e-6)||(Math.abs(line.get_ponl(a,this.ac))<1e-6)||(Math.abs(line.get_ponl(a,this.bc))<1e-6))//判断点a是否在三角形线上
return true;
return false;
}
//----------------------------------------------------------
/* 输入:直线上的两个点 point,triangle
* 输出: boolean
* 功能:判断直线ab与三角形cde是否有交点
*/
public boolean is_exist_interset (point a,point b) {
line ab=new line();
ab.get_line(a,b);
point c = this.a;//三角形其中一点
point d = this.b;
point e = this.c;
if((!line.is_interset(ab,c,d))&&(!line.is_interset(ab,c,e))&&(!line.is_interset(ab,e,d))){//三角形的三个点与线段ab均没有交点,即三角形的三条线段均在线段ab同一端
return false;
}
return true;
}
//----------------------------------------------------------
/* 输入:直线 line
* 输出:交点个数0/1/2 int
* 功能:求直线ab与三角形cde的交点个数
*/
public int get_intersetion(line ab) {
point c = this.a;//三角形其中一点
point d = this.b;
point e = this.c;
if((!line.is_interset(ab,c,d))&&(!line.is_interset(ab,c,e))&&(!line.is_interset(ab,e,d)))//三角形的三个点与线段ab均没有交点,即三角形的三条线段均在线段ab同一端
return 0;
if(line.is_point_on_edge(c, ab)||line.is_point_on_edge(d, ab)||line.is_point_on_edge(e, ab)){//直线过三角形任一顶点
if(line.is_point_on_edge(c, ab)) {//c点在ab上
if(!line.is_interset(ab,d,e)) //d,e两点在同一侧
return 1;//交点只有一个
else
return 2;//交点有两个,其中一个交点为c/a重合点
}
if(line.is_point_on_edge(d, ab)) {
if(!line.is_interset(ab,c,e))
return 1;
else
return 2;
}
if(line.is_point_on_edge(e, ab)) {
if(!line.is_interset(ab,d,c))
return 1;
else
return 2;
}
}
return 2;//直线不过三角形的顶点
}
//----------------------------------------------------------
/* 输入:直线 line
* 输出:面积数组,从小到大返回 double[]
* 功能:获得直线ab分割三角形cde后的两个面积
*/
public double[] get_divided_area (line ab) {
point c=this.a;
point d=this.b;
point e=this.c;
line de=this.bc;
line ce=this.ac;
line cd=this.ab;
point inter;
point inter1;
point inter2;
double []S=new double[2];
if(line.is_point_on_edge(c, ab)||line.is_point_on_edge(d, ab)||line.is_point_on_edge(e, ab)){//直线过三角形任一顶点
if(line.is_point_on_edge(c,ab)){//c点在ab上,ab交三角形于点inter
inter=line.get_intersection(ab,de);//另外一个交点一定在线段de上
triangle cid=new triangle();
cid.a=c;
cid.b=inter;
cid.c=d;
S[0]=cid.get_area();
}else if(line.is_point_on_edge(d,ab)){//d点在ab上,ab交三角形于点inter
inter=line.get_intersection(ab,ce);//另外一个交点一定在线段ce上
triangle cid=new triangle();
cid.a=c;
cid.b=inter;
cid.c=d;
S[0]=cid.get_area();
// System.out.println("y");
// System.out.println(cid.b.x+" "+cid.b.y);
}else if(line.is_point_on_edge(e,ab)){//e点在ab上,ab交三角形于点inter
inter=line.get_intersection(ab,cd);//另外一个交点一定在线段cd上
triangle cie=new triangle();
cie.a=c;
cie.b=inter;
cie.c=e;
S[0]=cie.get_area();
}
}else {//直线不过三角形的顶点
if(!line.is_interset(ab,c,d)){//点c,d在同一侧
inter1=line.get_intersection(ce,ab);
inter2=line.get_intersection(de,ab);
triangle eii=new triangle();
eii.a=e;
eii.b=inter1;
eii.c=inter2;
S[0]=eii.get_area();
}else if(!line.is_interset(ab,c,e)) {//点c,e在同一侧
inter1=line.get_intersection(cd,ab);
inter2=line.get_intersection(de,ab);
triangle dii=new triangle();
dii.a=d;
dii.b=inter1;
dii.c=inter2;
S[0]=dii.get_area();
}else if(!line.is_interset(ab,d,e)) {//点d,e在同一侧
inter1=line.get_intersection(cd,ab);
inter2=line.get_intersection(ce,ab);
triangle cii=new triangle();
cii.a=c;
cii.b=inter1;
cii.c=inter2;
S[0]=cii.get_area();
}
}
S[1]=this.get_area()-S[0];
//System.out.println(S[0]);
Arrays.sort(S);//升序排列
return S;
}
}
3-7-1 点线形系列1-计算两点之间的距离
import java.util.Scanner;
public class Main{
public static void main(String args[]){
Scanner input=new Scanner(System.in);
String s=input.nextLine();
if(!point.islegal(s,2)){
System.out.print("Wrong Format");
return;
}
if(point.get_length(s)!=2){
System.out.print("wrong number of points");
return;
}
point m=new point();
point n=new point();
m.get_point(s, 1);//获得点
n.get_point(s, 2);
System.out.print(m.distance(n));
}
}
//下面为点的类
SourceMonitor的生成报表内容:
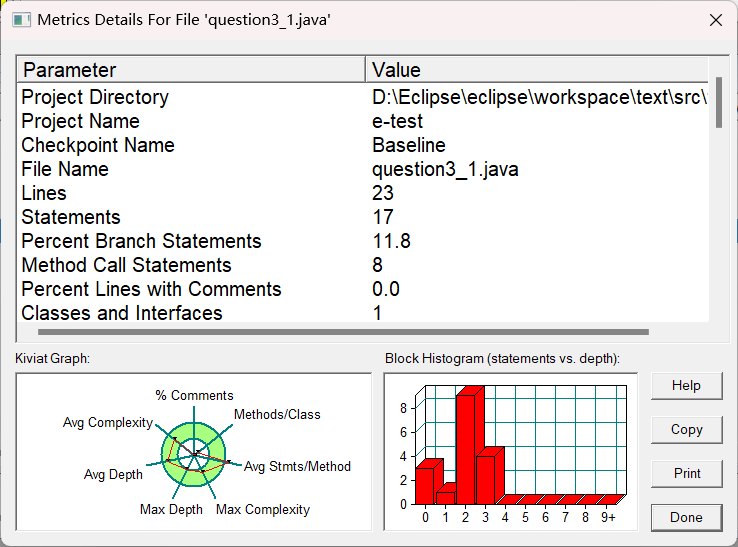
分析:判断字符串的合法性时用到了正则表达式。代码各类指标都良好,平均复杂度为3。
3-7-2 点线形系列2-线的计算
源码:
import java.util.Scanner;
public class Main{
public static void main(String args[]){
Scanner input = new Scanner(System.in);
String s=input.nextLine();
char ch0=s.charAt(0);
char ch1=s.charAt(1);
s=s.substring(2);
if(ch0<'1'||ch0>'5'||ch1!=':'||!point.islegal(s,2)){
System.out.print("Wrong Format");
return ;
}
point a = new point();
point b = new point();
point c = new point();
point d = new point();
a.get_point(s,1);
b.get_point(s,2);
line ab = new line ();
line bc = new line ();
line cd = new line ();
ab.get_line(a,b);
switch(ch0){
case '1':
if(point.get_length(s)!=2){
System.out.print("wrong number of points");
return ;
}
if(a.is_coi(b)){//判断两点是否相等
System.out.print("points coincide");
return ;
}
if(!ab.slope_exist()){//判断斜率是否存在
System.out.print("Slope does not exist");
return ;
}
System.out.print(ab.slope_calculation());
break;
case '2':
if(point.get_length(s)!=3){
System.out.print("wrong number of points");
return ;
}
c.get_point(s,3);
bc.get_line(b,c);
if(a.is_coi(b)||a.is_coi(c)||b.is_coi(c)){//判断任意两点是否相等
System.out.print("points coincide");
return ;
}
System.out.print(line.ptol_dis(a, bc));
break;
case '3':
if(point.get_length(s)!=3){
System.out.print("wrong number of points");
return ;
}
c.get_point(s,3);
bc.get_line(b,c);
if(a.is_coi(b)||a.is_coi(c)||b.is_coi(c)){//判断任意两点是否相等
System.out.print("points coincide");
return ;
}
if(line.ptol_dis(a, bc)==0){
System.out.print("true");
}else{
System.out.print("false");
}
break;
case '4':
if(point.get_length(s)!=4){
System.out.print("wrong number of points");
return ;
}
c.get_point(s,3);
d.get_point(s,4);
cd.get_line(c,d);
if(a.is_coi(b)||a.is_coi(c)||a.is_coi(d)||b.is_coi(c)||b.is_coi(d)||c.is_coi(d)){//判断任意两点是否相等
System.out.print("points coincide");
return ;
}
if(!ab.slope_exist()&&!cd.slope_exist()){
System.out.print("true");
return ;
}
if(!ab.slope_exist()||!cd.slope_exist()){
System.out.print("false");
return ;
}
if(ab.slope_calculation()==cd.slope_calculation()){
System.out.print("true");
return ;
}else{
System.out.print("false");
return ;
}
case '5':
if(point.get_length(s)!=4){
System.out.print("wrong number of points");
return ;
}
c.get_point(s,3);
d.get_point(s,4);
cd.get_line(c,d);
if(a.is_coi(b)||a.is_coi(c)||a.is_coi(d)||b.is_coi(c)||b.is_coi(d)||c.is_coi(d)){//判断任意两点是否相等
System.out.print("points coincide");
return ;
}
if(line.is_parallel(ab, cd)){
System.out.print("is parallel lines,have no intersection point");
return ;
}
point jiaodian=new point();
jiaodian = line.get_intersection(ab,cd);
System.out.print(jiaodian.x+","+jiaodian.y+" ");
if(line.is_interset(ab,c,d)){
System.out.print("true");
}else{
System.out.print("false");
}
break;
}
}
}
//下面为点类
SourceMonitor的生成报表内容:
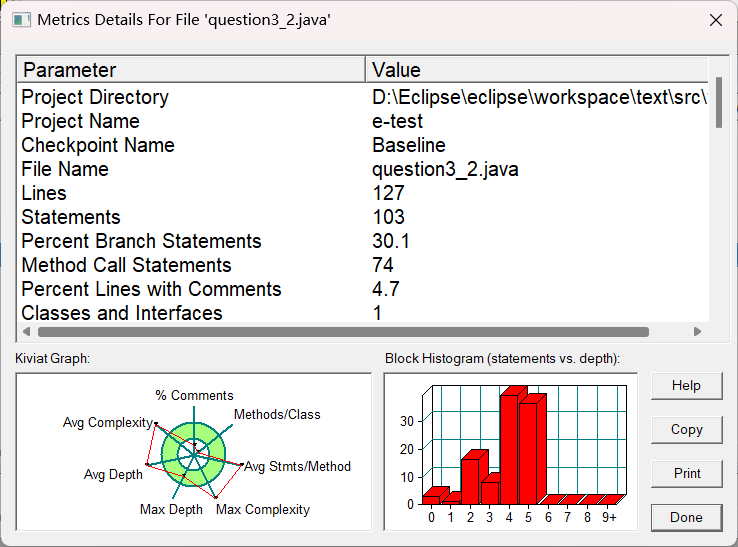
分析:代码主架构是switch里面有太多的if/else判断,导致部分指标不合格。
3-7-3 点线形系列3-三角形的计算
源码:
importxu java.util.Scanner;
public class Main{
public static void main(String args[]){
Scanner input = new Scanner(System.in);
String s=input.nextLine();
char ch0=s.charAt(0);
char ch1=s.charAt(1);
s=s.substring(2);
if(ch0<'1'||ch0>'5'||ch1!=':'||!point.islegal(s,2)){
System.out.print("Wrong Format");
return ;
}
triangle abc=new triangle();
triangle bcd=new triangle();
triangle abd=new triangle();
triangle acd=new triangle();
triangle cde=new triangle();
point a = abc.a;
point b = abc.b;
line ab = abc.ab;
double zhouchang;//周长
double S;//总面积
double []DS=new double[2];//分割面积
point bar=new point();//重心
double S1,S2,S3;//总面积
switch(ch0){
case '1':
if(point.get_length(s)!=3){
System.out.print("wrong number of points");
return ;
}
abc.get_triangle(s,1,2,3);//需要先判断点的个数是否有三个,否则可能会遇到数组问题,如只输入两个点时三角形类的初始化会出错
if(!abc.legal_form()){//判断能否构成三角形
System.out.print("data error");
return ;
}
if(abc.is_iso()) {//是否为等腰三角形
if(abc.is_equ()) {//是否为等边三角形
System.out.print("true true");
}else {
System.out.print("true false");
}
}else {
System.out.print("false false");
}
break;
case '2':
if(point.get_length(s)!=3){
System.out.print("wrong number of points");
return ;
}
abc.get_triangle(s,1,2,3);
if(!abc.legal_form()){//判断能否构成三角形
System.out.print("data error");
return ;
}
zhouchang=abc.get_perimeter();//获取周长
S=abc.get_area();//获取面积
bar=abc.get_gra();//获取重心
zhouchang=triangle.round(zhouchang, 6);//保留六位小数,多余位数四舍五入
S=triangle.round(S, 6);
bar.x=triangle.round(bar.x, 6);
bar.y=triangle.round(bar.y, 6);
System.out.print(zhouchang+" "+S+" "+bar.x+","+bar.y);
break;
case '3':
if(point.get_length(s)!=3){
System.out.print("wrong number of points");
return ;
}
abc.get_triangle(s,1,2,3);
if(!abc.legal_form()){//判断能否构成三角形
System.out.print("data error");
return ;
}
if(abc.compare_90angle()=='=')//直角三角形
System.out.print("false true false");
if(abc.compare_90angle()=='>')//钝角三角形
System.out.print("true false false");
if(abc.compare_90angle()=='<')//锐角三角形
System.out.print("false false true");
break;
case '4':
if(point.get_length(s)!=5){
System.out.print("wrong number of points");
return ;
}
cde.get_triangle(s,3,4,5);
abc.get_triangle(s,1,2,3);
a = abc.a;
b = abc.b;
ab.get_line(a,b);
if(a.is_coi(b)){//判断两点是否相等
System.out.print("points coincide");
return ;
}
if(!cde.legal_form()){//判断能否构成三角形
System.out.print("data error");
return ;
}
if(cde.is_line_on_edge(a, b)){//直线ab是否在三角形cde上
System.out.print("The point is on the edge of the triangle");
return ;
}
if(cde.get_intersetion(ab)==0) {
System.out.print(0);
return ;
}else if(cde.get_intersetion(ab)==1) {
System.out.print(1);
return ;
}else if(cde.get_intersetion(ab)==2) {
System.out.print(2+" ");
DS=cde.get_divided_area(ab);
System.out.print(triangle.round(DS[0], 6)+" "+triangle.round(DS[1], 6));
return ;
}
break;
case '5':
if(point.get_length(s)!=4){
System.out.print("wrong number of points");
return ;
}
bcd.get_triangle(s,2,3,4);
abc.get_triangle(s,1,2,3);
acd.get_triangle(s,1,3,4);
abd.get_triangle(s,1,2,4);
if(!bcd.legal_form()){//判断能否构成三角形
System.out.print("data error");
return ;
}
if(bcd.is_point_on_edge(a)){//判断点a是否在三角形线上
System.out.print("on the triangle");
return ;
}
S1=abc.get_area();
S2=acd.get_area();
S3=abd.get_area();
S=bcd.get_area();
//System.out.println(S1+" "+S2+" "+S3+" "+S);
if(S1+S2+S3-S<1e-12){
System.out.print("in the triangle");
return ;
}else {
System.out.print("outof the triangle");
return ;
}
}
}
}
//下面为点,线,三角形类
SourceMonitor的生成报表内容:
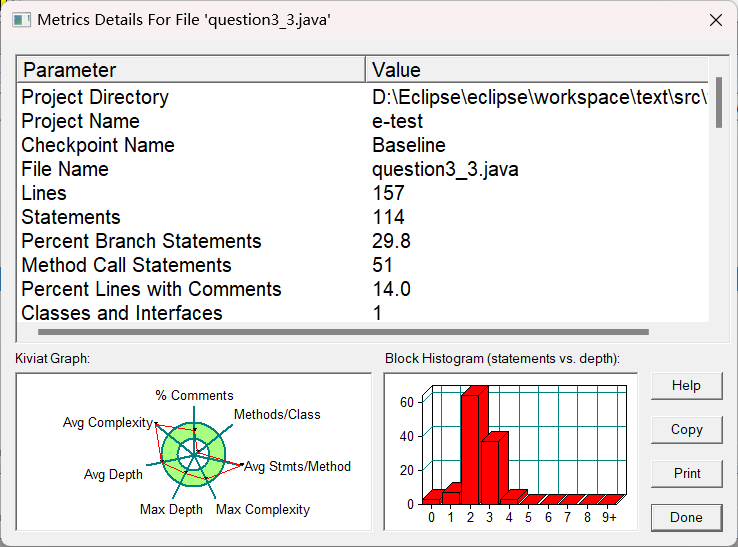
分析:主要问题和上面类似,不过平均复杂度更小。
采坑心得:
1-7-2 长度质量计量单位换算
需要将doule类型转化成float类型后输出,如:
System.out.print((float)zl +" "+ (float)cd);
1-7-4 房产税费计算2022
输出时需要将结果转化为float类型,切忌不要出现(flaot)c*100.0,先将结果括起来再进行类型转换,或者先转化为double类型:
double f=b*5.0;//印花税
double g=d*3.0;//交易费
double h=d*1.36;//测绘费
System.out.print(" "+(float)f+" "+(float)g+" "+(float)h);
1-7-6 学号识别
建议用字符串输入,不要用int,要不然会变得不幸,别问我为什么知道。
1-7-9 二进制数值提取
输入区分使用next和nextLine,个人觉得nextLine会更常用,因为要判别空格等非法字符。
1-7-7 判断三角形类型
...PTA排序出错了。注意精度问题,判断是否为直角三角形:
Math.abs(a*a+b*b-c*c)<0.1//勾股定理
2-7-2 串口字符解析
注意输入的是字符串,进行单个字符比较时加上单引号或者减去某个数值,如下:
if((n+1)%2==s[j]-48&&s[j+1]!='1')//判断奇校验位和结束位
3-7-3 点线形系列3-三角形的计算
保留6位小数,且多余部分采用四舍五入规则进到最低位,参考如下:
S1=(double)Math.round(S1*Math.pow(10,6))/Math.pow(10,6);
涉及到0值判断的都应该考虑精度问题:
if(S1+S2+S3-S<1e-12)//面积相等
改进建议
可以将一些复用性较强的代码封装进自己的编辑器中,比如第三次大作业的点类,线类,三角形类都分别对应了三道小题,前两次作业基本上是简单的输入和输出,复用性不高,可以略过。
总结
1.前两次作业是练手的,目的是熟悉java基本语法;但是第三次作业工作量会剧增,而且类与类之间的联系以及类方法的复用性会增强,如果不对复用性强的代码封装成类,那么Main里面的代码将会变得特别混乱且长,你可能在第一个小问里写过同样的代码,下一问又要用上,没写类只能复制粘贴,而且观感特别不好,因为隔一段时间再去看根本不知道这部分代码实现了啥功能,我对此深有体会,因为我这三次作业都是一股脑全写在Main里面,提交通过后再把全部代码全看懂了再进行封装,花费时间太长了。
2.java时面向对象,而C是面向过程的,需要从C的编码习惯慢慢变为java的编码习惯,这个转化过程是漫长且煎熬的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号