字典树

字典树

　　在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

　　字典树设计的核心思想是空间换时间，所以数据结构本身比较消耗空间。trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

　　如图，可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子，$\mathrm{1\to 4\to 8\to 12 表示的就是字符串 caa。}$

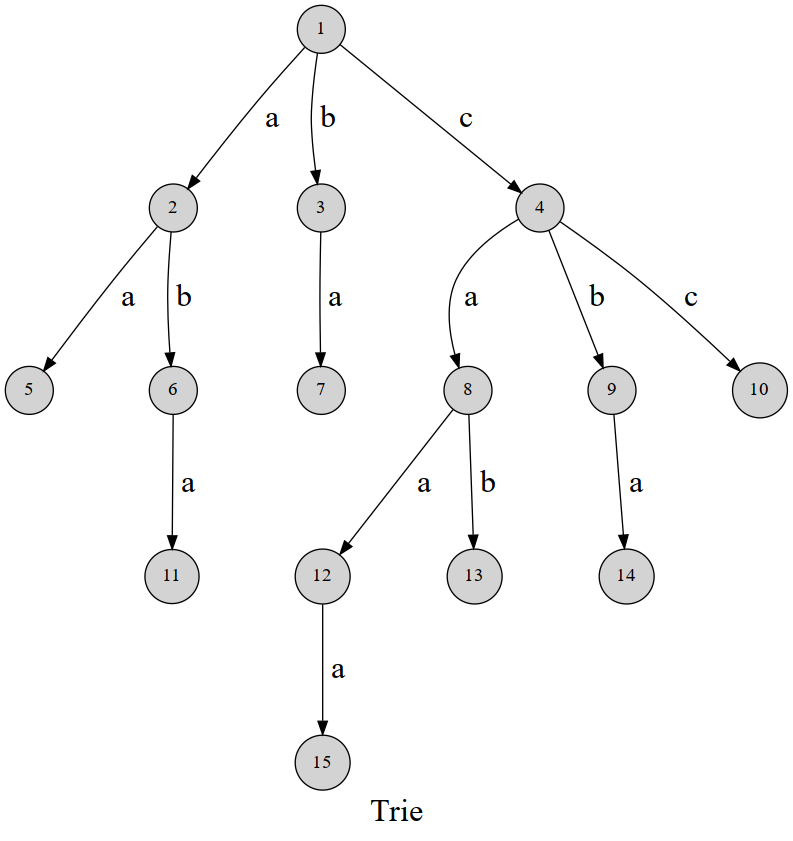
字典树的性质

1. 根节点（Root）不包含字符，除根节点外的每一个节点都仅包含一个字符；
2. 从根节点到某一节点路径上所经过的字符连接起来，即为该节点对应的字符串；
3. 任意节点的所有子节点所包含的字符都不相同；

Trie 关键词查找过程

1. 每次从根结点开始搜索；
2. 获取关键词的第一个字符，根据该字符选择对应的子节点，转到该子节点继续检索；
3. 在相应的子节点上，获取关键词的第二个字符，进一步选择对应的子节点进行检索；
4. 以此类推，进行迭代过程；
5. 在某个节点处，关键词的所有字母已被取出，则读取附在该节点上的信息，查找完成。

关键词的插入和查找过程的时间复杂度均为 O(key_length)，空间复杂度 O(ALPHABET_SIZE * key_length * N) ，其中 N 是关键词的数量。

Trie 的应用

• 字符串检索：事先将已知的一些字符串（字典）的有关信息保存到 Trie 里，查找另外一些未知字符串是否出现过或者出现频率。
• 字符串最长公共前缀：Trie 利用多个字符串的公共前缀来节省存储空间，反之，当我们把大量字符串存储到一棵 Trie 上时，我们可以快速得到某些字符串的公共前缀。
• 排序：Trie 树是一棵多叉树，只要先序遍历整棵树，输出相应的字符串，便是按字典序排序的结果。
• 作为其他数据结构和算法的辅助结构：如后缀树，AC自动机等，AC自动机也可以理解为在tire树上进行kmp。

代码实现

tire模板

struct trie {
  int nex[100000][26], cnt;
  bool exist[100000];  // 该结点结尾的字符串是否存在

  void insert(char *s, int l) {  // 插入字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) nex[p][c] = ++cnt;  // 如果没有，就添加结点
      p = nex[p][c];
    }
    exist[p] = 1;
  }
  bool find(char *s, int l) {  // 查找字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) return 0;
      p = nex[p][c];
    }
    return exist[p];
  }
};

 

检索字符串

对所有名字建 trie，再在 trie 中查询字符串是否存在、是否已经点过名，第一次点名时标记为点过名。

#include <cstdio>

const int N = 500010;

char s[60];
int n, m, ch[N][26], tag[N], tot = 1;

int main() {
  scanf("%d", &n);

  for (int i = 1; i <= n; ++i) {
    scanf("%s", s + 1);
    int u = 1;
    for (int j = 1; s[j]; ++j) {
      int c = s[j] - 'a';
      if (!ch[u][c]) ch[u][c] = ++tot;
      u = ch[u][c];
    }
    tag[u] = 1;
  }

  scanf("%d", &m);

  while (m--) {
    scanf("%s", s + 1);
    int u = 1;
    for (int j = 1; s[j]; ++j) {
      int c = s[j] - 'a';
      u = ch[u][c];
      if (!u) break;  // 不存在对应字符的出边说明名字不存在
    }
    if (tag[u] == 1) {
      tag[u] = 2;
      puts("OK");
    } else if (tag[u] == 2)
      puts("REPEAT");
    else
      puts("WRONG");
  }

  return 0;
}

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define TREE_WIDTH 256

#define WORDLENMAX 128

struct trie_node_st {
        int count;
        int pass; //add a count for the part-include for example 'this is' then the 'is' is hited two times 
        struct trie_node_st *next[TREE_WIDTH];
};

static struct trie_node_st root={0, 0, {NULL}};

static const char *spaces=" \t\n/.\"\'()";

void myfree(struct trie_node_st * rt)
{
    for(int i=0; i<TREE_WIDTH; i++){
        if(rt->next[i]!=NULL){
            myfree(rt->next[i]);
            rt->next[i] = NULL;
        }
    }
    free(rt);
    return;
}

static int
insert (const char *word)
{
        int i;
        struct trie_node_st *curr, *newnode;

        if (word[0]=='\0'){
                return 0;
        }
        curr = &root;
        for (i=0; ; ++i) {
                if (word[i] == '\0') {
                        break;
                }
                curr->pass++;//count
                if (curr->next[ word[i] ] == NULL) {
                        newnode = (struct trie_node_st*)malloc(sizeof(struct trie_node_st));
                        memset (newnode, 0, sizeof(struct trie_node_st));
                        curr->next[ word[i] ] = newnode;
                } 
                curr = curr->next[ word[i] ];
        }
        curr->count ++;

        return 0;
}

static void
printword (const char *str, int n)
{
        printf ("%s\t%d\n", str, n);
}

static int
do_travel (struct trie_node_st *rootp)
{
        static char worddump[WORDLENMAX+1];
        static int pos=0;
        int i;

        if (rootp == NULL) {
                return 0;
        }
        if (rootp->count) {
                worddump[pos]='\0';
                printword (worddump, rootp->count+rootp->pass);
        }
        for (i=0;i<TREE_WIDTH;++i) {
                worddump[pos++]=i;
                do_travel (rootp->next[i]);
                pos--;
        }
        return 0;
}

int
main (void)
{
        char *linebuf=NULL, *line, *word;
        size_t bufsize=0;
        int ret;

        while (1) {
                ret=getline (&linebuf, &bufsize, stdin);
                if (ret==-1) {
                        break;
                }
                line=linebuf;
                while (1) {
                        word = strsep (&line, spaces);
                        if (word==NULL) {
                                break;
                        }
                        if (word[0]=='\0') {
                                continue;
                        }
                        insert (word);
                }
        }

        do_travel (&root);

        free (linebuf);

    for(int i=0; i<TREE_WIDTH; i++){
        if(root.next[i]!=NULL){
            myfree(root.next[i]);
        }
    }

        exit (0);
}