【算法】前缀树
基本内容
以树的方式存储字符串的数据结构,方便字符串的查找及判断是否为某一字符串的前缀
题目要求:判断一组字符串中是否存在某一字符串是另一字符串的前缀。例如在{“911”, “91140”,“20”,“912”}中,“911”是“91140”的前缀
- 基本思想
将字符串的每一个元素视为一个节点,例如“911”中将“9”,“1”,“1”视为不同的节点。依次将所有字符串元素进行存储。
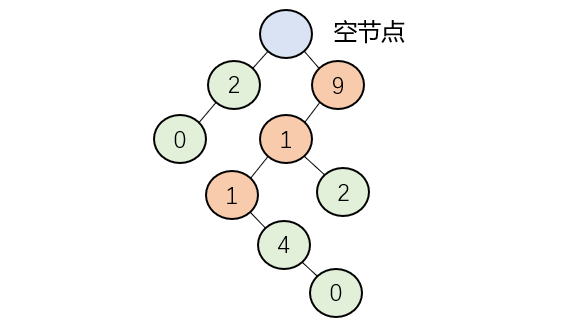
-
变量解释
❗ ❗ ❗ 一个元素就是一个节点,只有不同字符串的元素重复路径的时候才属于同一节点
N:记录一共最多可能有多少个节点;son:二维数组,son[N] [10],记录所有节的子节点的索引号idx,第二列为10是因为数字节点的子节点最多是10个,若是字母字符串的话应该是son[N] [26]cnt:记录第idx个节点是否为某一字符串的结尾节点idx:当前的节点索引号(节点通过数组存储) -
解题代码
strs = ["911", "91140", "20", "912"]
for s in strs:
p = 0 # 表示头节点
for i in range(len(s)):
if son[p][int(s[i])] == 0: # 为0表示当前没有该节点,idx为该节点的索引
idx += 1
son[p][int(s[i])] = idx
p = son[p][int(s[i])] # 更新p为下一元素的节点索引
# 判断是否为其他字符串的前缀的两种情况
# ① 当前节点是其他字符串的结束节点 ② 其他字符串的节点是当前字符串的结束节点
if cnt[p] != 0 or (i == len(s) - 1 and son[p][int(s[i])] != 0):
flag = True
print("NO")
break
cnt[p] += 1 # 以索引号为p的节点结尾的字符串加1,可以统计有多少个相同字符串
if not flag:
print("YES")
- 核心代码
前缀树核心代码主要是插入以及查询操作
插入操作
def insert(word): # 单词数据
for char in word:
u = ord(char) - ord('a')
if son[p][u] == 0:
idx += 1
son[p][u] = idx
p = son[p][u]
cnt[p] = 1 # 标记当前节点为结束节点
查询操作
def query(word):
p = 0
for char in word:
u = ord(char) - ord('a')
if son[p][u] != 0:
p = son[p][u]
else:
break #没有该单词
- 总结
- 前缀树是一种以空间换时间的数据结构
cnt数组不仅仅可以用于记录是否为字符串的结束节点,还可以记录相同字符串的个数- 在洛谷上用python代码提交会出现
TLE
题目
要求:在一组数找到两个数的最大异或值,以长度为3的数字为例子,当与“001”配对的能达到最大异或值的数字为“110”,即为反码
思路:从最高位开始,尽量找到与当前位数为反码的
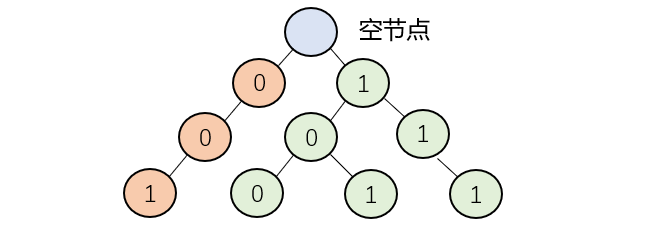
例子:在["001","101","100","111"] 中找到与 “111” 最大的异或对,从最高位开始,存在依次与
11互为反码的00节点,但在该路径中到了第三层不存在与1互为反码的0节点,因此只能继续选择1节点,因此最后能与111组成的最大异或对为001.
解法1:使用排序操作
class Solution:
def longestWord(self, words: List[str]) -> str:
N = 300010
cnt = [0] * N
son = [[0 for _ in range(26)] for _ in range(N)]
idx = 0
words.sort() # 排序以确保字典序最小的优先
Vmax = 0
res = ""
for word in words:
p = 0
valid = True # 标记当前单词是否有效
for i, char in enumerate(word):
u = ord(char) - ord('a')
if i < len(word) - 1 and cnt[son[p][u]] == 0: # 如果目前单词没有前缀停止加入(因为先用sort排序了)
valid = False
break
if son[p][u] == 0:
idx += 1
son[p][u] = idx
p = son[p][u]
# 检查当前单词是否是最长的可构建单词
if valid:
cnt[p] = 1 # 标记当前节点为结束节点
if len(word) > Vmax:
Vmax = len(word)
res = word
return res
解法2:不使用排序操作,先将所有word加入,再依次遍历查询
class Solution:
def longestWord(self, words: List[str]) -> str:
N = 30010
cnt = [0] * N
son = [[0 for _ in range(26)] for _ in range(N)]
idx = 0
Vmax = 0
res = ""
for word in words:
p = 0
for char in word:
u = ord(char) - ord('a')
# 检查是否可以构建当前前缀
if son[p][u] == 0:
idx += 1
son[p][u] = idx
p = son[p][u]
cnt[p] = 1 # 标记当前节点为结束节点
for word in words:
p = 0
valid = True
if len(word) < Vmax:
continue
for char in word:
u = ord(char) - ord('a')
if cnt[son[p][u]] != 0:
p = son[p][u]
continue
else:
valid = False
break
if valid and len(word) > Vmax:
Vmax = len(word)
res = word
elif valid and len(word) == Vmax:
if word < res:
res = word
return res



 浙公网安备 33010602011771号
浙公网安备 33010602011771号