排列组合

 排列：从 n个元素的集合 S 中，有序的选出 r 个元素，叫做 S  的一个 r 排列

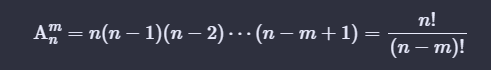
排列数的性质：

第一条性质：(n*(n-1)*...*2*1)/((n-1-m+1)*...*2*1)=n!/(n-m)!;

第二条性质：m*(n-1)!/(n-m)!+(n-1)!/(n-1-m)!=(n-m+m)*(n-1)!/(n-m)!=n!/(n-m)!

 组合：

从 n 个元素的集合 S 中，无序的选出 r 个元素，叫做 S 的一个 r 组合。

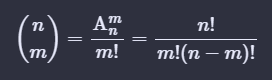
组合数的性质：

 乘法递推组合数（时间复杂度o(n)）:

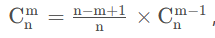
 根据以上递推式，又因为边界c(n,0)=1，可以得出：

c[0] = 1;
for (register int i = 1; i * 2 <= n; i++) {
    c[i] = (n - i + 1) * c[i - 1] / i;//必须先乘后除，不然可能会除不开
    c[n - i] = c[i];//利用对称性质，减少时间复杂度
}

register 声明的变量是直接放在cpu的寄存器当中，而非就是通过内存寻址访问，这样就可以大大的提高程序的运行效率，还需要注意，register 声明变量只能在主函数或自定义内部。注意：是内部，定义在外面是会报错的。

 

以上仅限数较小时使用。

 

当数较大时，题目可能要求取模，需要用到逆元。

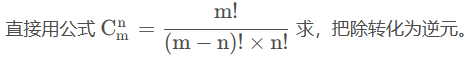
const int N = 1e6 + 7, mod = 1e9 + 7;
int n, m, k, t;
int inv[N];//逆元
int fact[N], infact[N];//阶乘结果，阶乘的逆元的结果

void init(int n)
{
    fact[0] = 1;//组合数c(n,0)=1;
    infact[0] = 1;//组合数为1的逆元为1
    inv[1] = 1;//1的逆元为1；
    for (int i = 2; i <= n; ++i)//先将1-n的所有逆元递推出来
        inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
    for (int i = 1; i <= n; ++i) {
        fact[i] = 1ll * fact[i - 1] * i % mod;
        infact[i] = 1ll * infact[i - 1] * inv[i] % mod;
        //每次除以一个数的mod就相当于乘这个数在该mod状态下的逆元
    }
}
int C(int n, int m)//无序
{
    if (n < m) return 0;
    if (m == 0 || n == m) return 1;
    return ((1ll * fact[n] % mod * infact[m] % mod) % mod * infact[n - m] % mod) % mod;
}

也可以利用此方法求排列数：

int A(int n, int m)//有序
{
    if (n < m || m < 0)return 0;
　　return fact[n] % mod * infact[n - m] % mod;
}

对组合数取模还有一个叫卢卡斯定理。。。之后再学吧。。。整理一晚上排列组合了。

 再挂一个二项式定理：

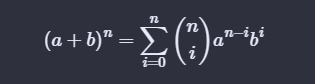
 收工。。。。。。。。。。。