平面图

---

✔️1. 平面图的定义及性质

定义：一个图若能以除顶点外任何边相互不交叉的形式画出(此时的图也称为平面嵌入或平面表示)，则为平面图

具有以下性质：
🔶 \(K_5,K_{3,3}\) 非平面图
🔶 环与平行边对平面图没有影响
🔶 子图非平面图\(\Rightarrow\)原图非平面图，原图为平面图\(\Rightarrow\)子图为平面图

面的次数：面G被包围的回路组(除下面一个例子)的长度，记作\(\deg(G)\)

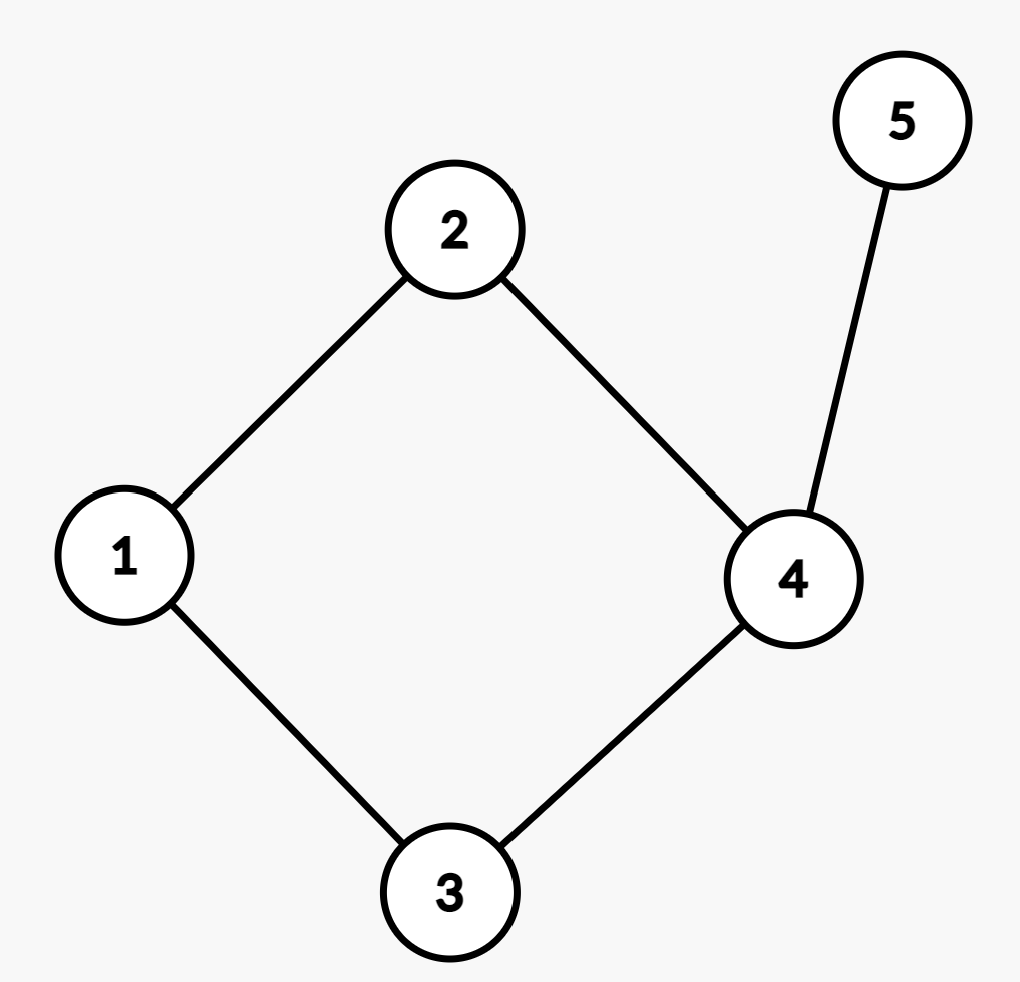
该图中\(\color{#39BAE8}{\boxed{\deg(G外)=6, \deg(G内)=4}}\),因为对于G外而言，包围它的回路为1245431
🌈回路组：所有包围该面的回路组成的集合

🛩️重要性质：

\[\sum\deg(G_i)=2m(边数) \]

解释：一条边为两个面贡献(面的)次数

---

✔️2. Eular定理

内容：任意的连通平面图(可以有重边/自环)

\[\mathrm{点(n)-边(m)+面(r)=2} \]

🌈 m = 1时 显然成立

🌈 假设m = k时 成立

🌈 m = k + 1时，
🔎 如果G为树，只需要删除树叶就能转化为上一个状态(m=k)，且有
$$ (n-1)-(m-1)+r=2$$
🔎 如果G不为树，则必存在环，我们只需要删掉环的一条边，即可转化为上一个状态
$$ n-(m-1)+r-1=2$$

推论1 ： 任意平面图，有\(\displaystyle{n-m+r=p(G)+1}\)

推论2 ：(判断非平面图)设G为连通的平面图，且每个面的次数至少为l(\(l\geq3\))，则

\[m\leq\frac{l}{l-2}(n-2) \]

注：事实上这个定理告诉我们一个成熟的平面图应避免边数过多

\[\begin{cases} 2m=\sum deg(G_i)\geq lr\\\\ n-m+r=2 \end{cases} \]

消去r即可(毕竟对于一个非平面嵌入的平面图，统计r是很难的)
**
注：\(\color{#400D12}{\boxed{l\ne2}}\)正是因为分母不为0，没有其他意义~~~

推论2.1 ：对于任意的平面图，且每个面的次数至少为l(\(l\geq3\))，则

\[m\leq\frac{l}{l-2}(m-q-1) \]

其实就是\(\boxed{\color{#4d638c}{q+1}}\rightarrow\boxed{\color{#e38b73}{2}}\)

推论2. 2 ：设G是\(n\geq3\)阶m条边的简单平面图，则

\[m\leq3n-6 \]

❗极大平面图：G为n(\(\geq3\))阶简单连通的平面图，当且仅当每个面的次数都是3
❗G为极大平面图，则(证明只需要将3r=2m代入欧拉定理)：

\[m=3n-6 \]

显然，非连通图的话，边数m小于连通的时候，所以推论显然成立

---

✔️3. Kuratowski定理

同胚：(1). 两个图，同构或者 (2). 经过反复插入，删除后同构

收缩：将两个顶点合并，新顶点继承原两个顶点的所有边

定理1：1个图是平面图，当且仅当该图内不含与\(K_5,K_{3,3}\)同胚的子图
定理2：1个图是平面图，当且仅当它没有可以收缩到\(K_5,K_{3,3}\)的子图